
Visão Computacional
1. Representação de
imagens
2. Filtragem de imagens
3. Detecção de Bordas
4. Segmentação Simples
5. Crescimento de Regiões
6. Segmentação com
Filtros
7. Segmentação a Cores
8. Análise de Texturas
9. Análise de Texturas
Multiescalar
10. Redes Neurais
11. Morfologia Matemática
12. Convolução
13. Esqueletonização
14. Técnicas Estatísticas
15. Fractais
16. Reconhecimento de
Formas
17. Representação de
Objetos
18. Quadtrees e Octrees
19. Visão Estereo
20. Inteligência Artificial
21. Controle de qualidade
22. Robótica
23. Medicina
24. Sensoriamento remoto
Prof. Aldo von Wangenheim
Currículo...
Publicações
Pesquisa
Projetos
Ensino de Graduação
Ensino de Pós Graduação
Cursos
Técnicas Estatísticas para Reconhecimento e Deteção de Face
<Luciene de Oliveira
Marin>
<luciene@inf.ufsc.brl>
- Métodos de Correlação
- Métodos Baseados em Expansão Karhunen-Loeve
- Reconhecimento Usando Autofaces"
- Reconhecimento sob Condições de Visualização Gerais
- Reconhecimento Usando AutoCaracterísticas"
- Método Discriminante Linear - Fisherfaces"
- Método Baseado no Modelo Markov Escondido
- Misturas de Subespaços Linear Local
- Objetivo
- Considerações
- Algoritmo
- Imagens de Saída
- Desempenho
- Problemas e Críticas Apresentadas
- Implementação
Bibliografia
Introdução
A face humana é uma imagem fascinante, uma inspiração infinita para artistas a milhares de anos. Além disso, a habilidade para reconhecer faces e entender as emoções que elas transmitem é uma das mais importantes habilidades humanas. Bebês podem identificar a face de suas mães dentro de meia hora de nascimento, a maioria de nós é hábil para instantaneamente reconhecer milhares de pessoas, haja visto que Napoleão poderia reconhecer todos os soldados regulares de seu exército [PLH99]. Os maiores reconhecedores de padrão na maioria dos exemplos são humanos, mas ainda não entendemos como os humanos reconhecem padrões. Reconhecimento de padrão é o estudo de como máquinas podem observar o ambiente, aprender e distinguir padrões de interesse do que está sendo visto, verificar e justificar decisões sobre as categorias dos padrões [AKJ99]. A abordagem estatística para reconhecimento de padrão merece especial atenção pois é a que mais tem sido estudada e usada na prática. No que se refere ao projeto de um sistema de reconhecimento, os seguintes assuntos requerem cuidadosa atenção: definição de classes de padrões, absorção do ambiente, representação de padrão, extração e seleção de características, análise de cluster, projeto e aprendizagem de classificador, seleção de exemplos de treinamento e teste, e avaliação de desempenho. Apesar de quase cinqüenta anos de pesquisa e desenvolvimento neste campo, problemas comuns de reconhecimento de padrões complexos com orientação, localização e escala arbitrários encontram-se sem solução. Novas e emergentes aplicações, tais como mineração de dados, pesquisa na web, restauração de dados multimídia, reconhecimento de face e reconhecimento de letras escrita à mão, requerem técnicas robustas e eficientes de reconhecimento de padrão [AKJ99]. O objetivo deste trabalho consiste em pesquisar a respeito do emprego de técnicas estatísticas de processamento de imagens no reconhecimento de padrões relacionados a faces humanas. O mesmo apresenta também uma breve exposição a respeito da abordagem estatística para sistemas de detecção de face, pois ela também é essencial para se desenvolver algoritmos eficientes e robustos em sistemas completamente automáticos, capazes analizar informações de faces humanas [MHY99].Reconhecimento de Padrão
Reconhecimento automático, descrição, classificação, e agrupamento de padrões são problemas importantes em diversas disciplinas de engenharia e científicas tais como biologia, psicologia, medicina, marketing, visão computacional, inteligência artificial, e percepção de distância. Mas o que é um padrão? Defini-se um padrão como o oposto do caos; uma entidade, vagamente definida, a qual pode ser dada um nome . Por exemplo, um padrão poderia ser uma imagem de impressão digital, uma palavra escrita a mão, uma face humana, ou um sinal de voz. Dado um padrão, reconhecê-lo ou classificá-lo pode consistir de uma das seguintes tarefas: (i) classificação supervisionada (p.e. análise discriminante) na qual o padrão de entrada é identificado como um membro de uma classe pré-definida, ou seja, a classe é definida pelo projetista do sistema, (ii) classificação não supervisionada (p.e. clustering" - agrupamento) no qual o padrão é determinado por uma fronteira" de classe desconhecida, ou seja, as classes são aprendidas baseadas na similaridade dos padrões. As quatro abordagens mais conhecidas para reconhecimento de padrão são: (i) casamento de modelo", (ii) classificação estatística, (iii) casamento sintático ou estrutural", e (iv) redes neurais. Estes modelos não são necessariamente independentes e às vezes o mesmo método de reconhecimento de padrão existe com diferentes interpretações [AKJ99].Reconhecimento de Padrão Estatístico
O reconhecimento de padrão estatístico tem sido usado com sucesso para projetar uma quantidade de sistemas comerciais de reconhecimento. Na abordagem estatística, cada padrão é representado em termos de características, medidas ou atributos e é visto como um ponto em um espaço d-dimensional. O objetivo é escolher determinadas características que permitam a vetores padrão, pertencentes a diferentes categorias, ocupar regiões compactas e disjuntas em um espaço de características d-dimensional. A efetividade do espaço de representação (conjunto de características) é determinado por quão bem separados podem ser os padrões de diferentes classes. Dado um conjunto de padrões de treinamento de cada classe, o objetivo é estabelecer decisões de fronteiras no espaço de características, aos quais os padrões separados pertenceriam a diferentes classes. Na abordagem teórica de decisão estatística, a decisão de fronteiras é determinada por distribuições de probabilidade de padrões pertencentes a cada classe, a qual deve ser específica ou aprendida. Um sistema de reconhecimento é operado em dois modos: treinamento (aprendizagem) e classificação (teste) veja na Fig. 1.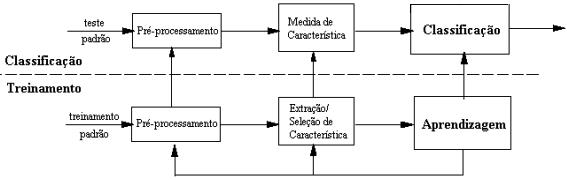
A função do
módulo de pré-processamento é retirar o padrão
de interesse de uma paisagem, remover ruídos, normalizar o padrão,
e qualquer outra operação a qual contribui na definição
de uma representação compacta do padrão. No modo treinamento,
o módulo de extração/seleção de características
procura características apropriadas para a representação
de padrões de entrada e o classificador é treinado para particionar
o espaço de características. O caminho de volta permite a
um projetista otimizar o pré-processamento e estratégias
de extração/seleção de características.
No modo classificação, o classificador treinado determina
o padrão de entrada para uma das classes de padrões sob considerações
baseadas na medidas das características. O processo de tomada de
decisão no reconhecimento de padrão estatístico pode
ser sumariado como segue. Um dado padrão está determinado
a uma das c categorias baseado em um vetor de d valores de característica ![]() .
As características tem uma densidade de probabilidade ou função
massa (dependendo se as características são contínuas
ou discretas) condicionada à classe de padrão. Assim um vetor
padrão
.
As características tem uma densidade de probabilidade ou função
massa (dependendo se as características são contínuas
ou discretas) condicionada à classe de padrão. Assim um vetor
padrão ![]() pertencente
a uma classe
pertencente
a uma classe![]() é visto com uma observação de extração
ao acaso de uma função de probabilidade classe-condicional
é visto com uma observação de extração
ao acaso de uma função de probabilidade classe-condicional ![]() .
Um número bem conhecido de regras de decisão, incluindo regra
de decisão Bayes, a regra da probabilidade máxima (a qual
pode ser vista como um caso particular de regra Bayes), e a regra Neyman-Peason
são eficazes para definir a decisão de fronteira. A regra
de decisão de Bayes "ótima" para a minimização
do risco (exceto valores da função de perda) pode ser declarado
como segue:
.
Um número bem conhecido de regras de decisão, incluindo regra
de decisão Bayes, a regra da probabilidade máxima (a qual
pode ser vista como um caso particular de regra Bayes), e a regra Neyman-Peason
são eficazes para definir a decisão de fronteira. A regra
de decisão de Bayes "ótima" para a minimização
do risco (exceto valores da função de perda) pode ser declarado
como segue:
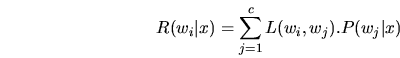
Ela determina o padrão
de entrada ![]() para a classe
para a classe ![]() para o qual o risco condicional é mínimo, onde a perda da
função implicada sobre
para o qual o risco condicional é mínimo, onde a perda da
função implicada sobre ![]() é determinada quando a classe verdadeira é
é determinada quando a classe verdadeira é ![]() e
e ![]() é a probabilidade posterior. No caso de função perda
é a probabilidade posterior. No caso de função perda ![]() ,
como definido na Eq. 2, o risco condicional torna-se a probabilidade condicional
de classificação errônea.
,
como definido na Eq. 2, o risco condicional torna-se a probabilidade condicional
de classificação errônea.
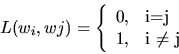
Para esta escolha da função
perda, a regra de decisão Bayes pode ser simplificada como segue:
Ela determina o padrão de entrada ![]() para a classe
para a classe ![]() se
se
![]()
Várias estratégias são utilizadas para projetar um classificador para um reconhecimento de padrão estatístico, dependendo da espécie de informação disponível sobre densidades de classe-condicional. Se todas as densidades de classe-condicional são completamente especificadas, então a regra de decisão Bayes ótima pode ser usada para projetar o classificador. Entretanto, densidades de classe-condicional são freqüentemente não conhecidas na prática e devem ser aprendidas dos padrões de treinamento disponíveis. Se a forma da densidade classe-condicional é conhecida (p. e. Gaussian multivariado), mas alguns dos parâmetros de densidades (p. e. vetores médio e matrizes de covariância) são desconhecidos, então nós temos um problema de decisão parametrizada. Uma estratégia comum para estes tipos de problemas é substituir os parâmetros desconhecidos na função densidade por seus valores estimados, resultando no então chamado classificador Bayes "plug-in". A estratégia Bayesiana ótima nesta situação requer informação adicional na forma de uma distribuição prévia nos parâmetros desconhecidos. Se a forma da densidade classe-condicional é não conhecida, então nós operamos em um modo não parametrizado. Neste caso, nós devemos ou estimar a função de densidade (p. e., abordagem Janela Parzen) ou diretamente construir a decisão de fronteira baseada no treinamento dos dados (p. e., regra do k mais próximo vizinho). De fato, um perceptron multicamada pode ser visto como um método supervisionado não paramétrico o qual constrói uma decisão de fronteira. Outra dicotomia em reconhecimento de padrão estatístico é a do aprendizado supervisionado (chamado treinamento de exemplos) versus o aprendizado não supervisionado (não chamado de treinamento de exemplos). O chamado treinamento de exemplos representa a categoria ao qual o padrão pertence. Em um problema de aprendizado não supervisionado, algumas vezes o número de classes deve ser aprendido diante as estruturas de cada classe. As várias dicotomias que aparecem em reconhecimento de padrões estatísticos são mostradas na árvore de estruturas da Fig.2.
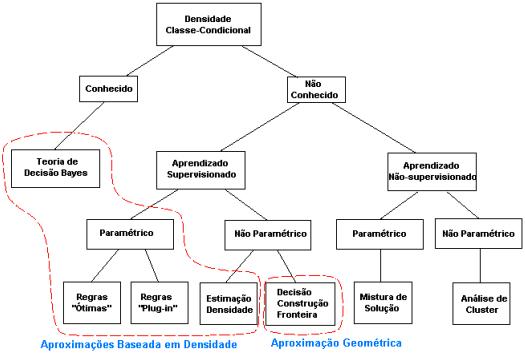
Como se percorre a árvore de cima para baixo e da esquerda para a direita, menos informações estão disponíveis para o projetista de sistema e como um resultado, a dificuldade de classificação dos problemas aumenta. Em alguns casos, a maioria das abordagens em reconhecimento de padrões estatístico (nós folhas da árvore da Fig. 2 ) são tentativas de implementar a regra de decisão Bayes. O campo de análise de cluster essencialmente trata com problemas de tomada de decisão no modo não paramétrico e aprendizado não supervisionado. Além disto, na análise de cluster o número de categorias ou clusters talvez nem mesmo sejam especificadas; a tarefa é descobrir uma categorização razoável dos dados (se alguma existir). Algoritmos de análise de cluster junto com várias técnicas para visualização e projeção de dados multi-dimensionais são também referidas como métodos de análise de dados exploratórios. Ainda outras dicotomias em reconhecimento de padrão estatístico podem ser baseadas se as decisões de fronteiras são obtidas diretamente (abordagem geométrica) ou indiretamente (abordagem baseada em densidade probabilística) como mostrado na Fig.2. A abordagem probabilística requer estimar a primeira função de densidade, e então construir as funções discriminantes as quais especificam as fronteiras de decisão. Por outro lado, a abordagem geométrica freqüentemente constrói fronteiras de decisão diretamente através de funções de custo fixo. Não é importante qual regra de classificação ou decisão é usada, ela deve ser treinada usando os exemplos de treinamento disponíveis. Como um resultado, o desempenho de um classificador depende de ambos o número de exemplos de treinamentos disponíveis bem como valores específicos de exemplos. Ao mesmo tempo, o objetivo de um projetista de sistema de reconhecimento é classificar exemplos de testes futuros os quais são provavelmente diferentes dos exemplos de treinamento. Então, otimizando um classificador para maximizar sua performance no conjunto de treinamento pode não sempre resultar na performance desejada em um conjunto de teste. A habilidade de generalização de um classificador refere-se para sua performance em classificar padrões testes os quais não foram usados durante o estágio de treinamento. Uma pobre habilidade de generalização de um classificador pode ser atribuída por qualquer um dos seguintes fatores: (i) o número de características é muito grande relativo ao número de exemplos de treinamento, (ii) o número de parâmetros desconhecidos associados com o classificador é grande (p. e., classificadores polinomial ou uma rede neural larga), e (iii) um classificador é intensivamente otimizado no conjunto de treinamento (treinamento demasiado - overtraining"); isto é análogo ao fenômeno de overfitting" em regressão quando existe muitos parâmetros livres. Overtraining tem sido investigado teoricamente por classificadores que minimizam a taxa de erro aparente (o erro no conjunto de treinamento). Estudos clássicos sobre capacidade e complexidade de classificadores (p. e. aqueles tendo muitos parâmetros independentes) podem ter uma larga capacidade, isto é eles são hábeis para representar muitas dicotomias para um conjunto de dados dado. Uma medida freqüentemente usada para a capacidade é o dimensionamento Vapnik-Chervonenkis (VC). Estes resultados podem também ser usados para mostrar algumas propriedades interessantes, por exemplo, a consistência do classificador fixo. O uso prático dos resultados sobre classificadores complexos foram inicialmente limitados porque os limites propostos no número requerido de exemplos de (treinamento) foram muito conservativos. No recente desenvolvimento de máquinas de vetor de suporte, entretanto, os resultados tem mostrado ser de total utilidade. A armadilha sobre adaptação de estimadores para o conjunto de treinamento dado é observado em muitos estágios de um sistema de reconhecimento de padrão, tais como redução de dimensionalidade, estimação de densidade, e projeto de classificador. Uma solução certa é sempre usar um conjunto de dados (conjunto teste) independente para avaliação. Na ordem de evitar a necessidade de ter muitos conjuntos testes independentes, estimadores são freqüentemente baseados em subconjuntos de dados rotados, preservando diferentes partes dos dados para otimização e avaliação [AKJ99].
Abordagens Estatísticas para o Reconhecimento de Face
O reconhecimento de face a partir de imagens fotográficas e imagens de vídeo está emergindo como uma atividade na área de pesquisa com numerosas aplicações comerciais e coação de lei. Estas aplicações requerem algoritmos robustos para reconhecimento de faces humanas sobre diferentes condições de iluminação, expressões faciais e orientações. Um esquema geral usado para reconhecimento de face é ilustrado na Fig. 3 [Nef96].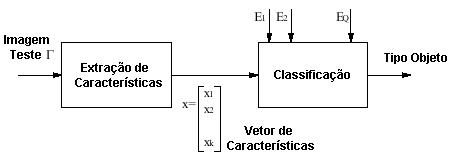
O vetor de características![]() extraído de uma imagem teste ( é comparado a cada um dos
vetores de características extraídos de todos os exemplos
de imagens de face
extraído de uma imagem teste ( é comparado a cada um dos
vetores de características extraídos de todos os exemplos
de imagens de face![]() e uma medida de similaridade no espaço de características
é usado para classificar a imagem entrada como uma das imagens de
exemplos. A razão de imagens de face classificadas corretamente
sobre o número total de faces classificadas pelo sistema de reconhecimento,
define o desempenho de reconhecimento (taxa de reconhecimento) do sistema.
Baseado na extração de características e técnicas
de classificação usadas, as abordagens de reconhecimento
de face segundo [Nef96] são:
e uma medida de similaridade no espaço de características
é usado para classificar a imagem entrada como uma das imagens de
exemplos. A razão de imagens de face classificadas corretamente
sobre o número total de faces classificadas pelo sistema de reconhecimento,
define o desempenho de reconhecimento (taxa de reconhecimento) do sistema.
Baseado na extração de características e técnicas
de classificação usadas, as abordagens de reconhecimento
de face segundo [Nef96] são:
- Parametrização geométrica
- Estatística
- Redes neurais
- Métodos de correlação
- Métodos de decomposição de valor singular
- Métodos baseados em expansão Karhune-Loeve
- Métodos baseados em discriminante linear Fisher
Métodos baseados em modelo de Markov escondido
A maioria direta dos procedimentos
usados para reconhecimento de face é o casamento entre as imagens
teste e um conjunto de treinamento de imagens baseado na medida de correlação.
O casamento técnico, neste caso é baseado na computação
do coeficiente de correlação-cruzada CN, definido por: Onde ![]() é a imagem a qual deve ser combinada com a template
é a imagem a qual deve ser combinada com a template![]() ,
, ![]() representa o produto pixel-por-pixel,
representa o produto pixel-por-pixel, ![]() é o operador médio e
é o operador médio e ![]() é o desvio padrão sobre a área sendo combinada. Esta
normalização reorganiza a template e a distribuição
de energia da imagem de forma que suas médias e variâncias
combinem. Entretanto, métodos baseados em correlação
são muito dependentes de iluminação, rotação
e escala. Os melhores resultados para a redução das variações
de iluminação foram obtidos usando intensidade de gradiente
é o desvio padrão sobre a área sendo combinada. Esta
normalização reorganiza a template e a distribuição
de energia da imagem de forma que suas médias e variâncias
combinem. Entretanto, métodos baseados em correlação
são muito dependentes de iluminação, rotação
e escala. Os melhores resultados para a redução das variações
de iluminação foram obtidos usando intensidade de gradiente![]() .
Porque o método de correlação é computacionalmente
muito caro, a dependência do reconhecimento sobre a resolução
da imagem tem sido investigada. Estudos mostram que o reconhecimento baseado
na correlação tem um bom nível de desempenho usando
templates pequenas de 36 x 36 pixeis [Nef96].
.
Porque o método de correlação é computacionalmente
muito caro, a dependência do reconhecimento sobre a resolução
da imagem tem sido investigada. Estudos mostram que o reconhecimento baseado
na correlação tem um bom nível de desempenho usando
templates pequenas de 36 x 36 pixeis [Nef96].
Reconhecimento Usando "Autofaces"
O método Autofaces tem sido implementado com o propósito de comparações, pois ele foi um dos melhores sucedidos dentre os algoritmos avaliados. Este método foi desenvolvido no M.I.T. por [Turk and Pentland, 1991] apud [Spi]. No qual é chamado Análise de Componente Principal onde poucos parâmetros são usados para representação, extraídos da face. Estes parâmetros são obtidos pela projeção da face sobre um sistema de coordenadas dados por autovetores" da matriz de covariância do conjunto de treinamento. Estes autovetores, imagens deles mesmos, são chamados autofaces" e transpõe um vetor de espaço chamado espaço face. Cada face é então codificada por meios de suas coordenadas no espaço face. O matching" de duas faces corresponde a um cálculo da distância Euclidiana entre suas representações do espaço de face [Spi]. O trabalho de [Li] apresenta uma nova abordagem para classificação de padrão chamada combinação linear mais próxima (NLC) para reconhecimento de face baseado em autoface. Ele assume que múltiplos vetores prototípicos são disponíveis através de classes, cada vetor começando de um ponto em um espaço autoface. Uma combinação linear de vetores prototípicos pertencentes a uma face classe é usada para definir uma medida de distância de um vetor"query" para a classe, a medida é definida como sendo a distância Euclidiana do "query" para a combinação linear mais próxima (portanto NLC). Isto contrasta a classificação do vizinho mais próximo (NN) onde um vetor query é comparado com cada vetor prototípico individualmente. Usando uma combinação linear de vetores prototípicos, ao invés de cada um deles individualmente, estende-se a capacidade de representação dos protótipos pela generalização, através de interpolação e extrapolação. Experimentos mostraram que isto conduz a melhores resultados do que os métodos de classificação existentes. A Fig. 4 ilustra o uso da técnica NLC para deduzir a posição de

Figura 4: (Linha Topo)Faces
sob mudanças no ângulo de visão. A face query ![]() (esquerda) está a um ângulo relativo central das duas faces
prototípicas
(esquerda) está a um ângulo relativo central das duas faces
prototípicas ![]() e
e ![]() ,
vistas a um ângulo direito e esquerdo respectivamente. (Linha Meio)
Faces sob mudanças de iluminação. A face query
,
vistas a um ângulo direito e esquerdo respectivamente. (Linha Meio)
Faces sob mudanças de iluminação. A face query ![]() (esquerda) é iluminada por uma luz à direita e é comparada
a duas faces prototípicas
(esquerda) é iluminada por uma luz à direita e é comparada
a duas faces prototípicas ![]() e
e ![]() ,
uma iluminada pela esquerda e outra pelo centro, respectivamente. (Linha
Inferior) Faces sob mudanças de expressões.
,
uma iluminada pela esquerda e outra pelo centro, respectivamente. (Linha
Inferior) Faces sob mudanças de expressões.
Este aprimoramento é
devido a representação NLC que expande a capacidade representacional
de protótipos de faces na base de dados: Variações
na iluminação, ângulo de visão e na expressão
entre imagens de faces prototípicas são consideradas por
variações em seus pesos que determinam a combinação
linear.
Reconhecimento sob Condições de Visualização Gerais
A Abordagem ParamétricaEsta abordagem extende a
capacidade do método autoface para reconhecimento de objetos em
imagem 3D sob diferentes condições de iluminação
e visualização. Dadas imagens de objetos tidas sob ![]() condições de visão e
condições de visão e![]() condições de iluminação, um conjunto de imagem
universal é construído o qual contém todos os dados
disponíveis. Desta maneira um simples espaço paramétrico"
descreve a identificação do objeto, bem como as condições
de visualização ou iluminação. A decomposição
autoface deste espaço é usada para extração
e classificação de características. Entretanto, na
ordem de garantir discriminação entre diferentes classes
de objeto o número de autovetores usados neste método é
incrementado, comparado ao método Autoface clássico [Nef96].
condições de iluminação, um conjunto de imagem
universal é construído o qual contém todos os dados
disponíveis. Desta maneira um simples espaço paramétrico"
descreve a identificação do objeto, bem como as condições
de visualização ou iluminação. A decomposição
autoface deste espaço é usada para extração
e classificação de características. Entretanto, na
ordem de garantir discriminação entre diferentes classes
de objeto o número de autovetores usados neste método é
incrementado, comparado ao método Autoface clássico [Nef96].
Baseada na decomposição
autoface, [Pentland et al] apud [Nef96] desenvolveu uma abordagem
baseada em autoespaço "view-based" para reconhecimento de faces
humanas sob condições gerais de visão. Dados indivíduos
sob ![]() diferentes visões, o reconhecimento é executado sob condições
gerais de visão. A abordagem view-based" é essencialmente
uma extensão da técnica autoface para múltiplos conjuntos
de autovetores, um para cada orientação de face. Para distribuir
as múltiplas visões, num primeiro estágio desta abordagem,
a orientação da face teste é determinada e o autoespaço
o qual melhor descreve a imagem de entrada é selecionado. Isto é
efetuado calculando o erro descrição residual (distância
do espaço de características: DFFS) para visão espaço.
Uma vez a visão apropriada sendo determinada, a imagem é
projetada sobre esta visão espaço e então reconhecida.
A abordagem view-based é computacionalmente mais intensiva do que
a abordagem paramétrica porque
diferentes visões, o reconhecimento é executado sob condições
gerais de visão. A abordagem view-based" é essencialmente
uma extensão da técnica autoface para múltiplos conjuntos
de autovetores, um para cada orientação de face. Para distribuir
as múltiplas visões, num primeiro estágio desta abordagem,
a orientação da face teste é determinada e o autoespaço
o qual melhor descreve a imagem de entrada é selecionado. Isto é
efetuado calculando o erro descrição residual (distância
do espaço de características: DFFS) para visão espaço.
Uma vez a visão apropriada sendo determinada, a imagem é
projetada sobre esta visão espaço e então reconhecida.
A abordagem view-based é computacionalmente mais intensiva do que
a abordagem paramétrica porque ![]() diferentes conjuntos de
diferentes conjuntos de ![]() projeções são requeridas (
projeções são requeridas (![]() é o número de autofaces selecionadas para representar cada
autoespaço). Entretanto, isto não implica que um fator de
tempo
é o número de autofaces selecionadas para representar cada
autoespaço). Entretanto, isto não implica que um fator de
tempo ![]() na
computação é necessariamente requerida. Calculando
progressivamente os coeficientes autovetores enquanto corta espaços
de visão alternativos, o custo do uso de
na
computação é necessariamente requerida. Calculando
progressivamente os coeficientes autovetores enquanto corta espaços
de visão alternativos, o custo do uso de ![]() autoespaços pode ser grandemente reduzido. Naturalmente, a representação
view-based pode render mais precisão de representação
do que o fundamento geométrico.
autoespaços pode ser grandemente reduzido. Naturalmente, a representação
view-based pode render mais precisão de representação
do que o fundamento geométrico.
No trabalho de [MP94], foi
apresentada uma abordagem para automaticamente determinar a orientação
da cabeça para construir um conjunto view-based de ![]() autoespaos separados, cada variação foi capturada de indivíduos
em uma visão comum. O autoespaço view-based é essencialmente
uma extensão da técnica autoface para múltiplos conjuntos
de autovetores, um para cada combinação de escala e orientação.
Alguém poderia pensar desta arquitetura como um conjunto pararelo
de observadores", cada um tentando explicar os dados da imagem com seu
conjunto de autovetores. Neste view-based, abordagem múltiplos-observadores,
o primeiro passo é determinar a localização e orientação
do objeto objetivo pela seleção do autoespao que melhor descreve
a imagem de entrada. Isto é efetuado pelo o cálculo do erro
descrição residual (a métrica distância-do-espaço-de-face")
usando cada um dos autovetores dos espaos de visão. Uma vez determinado
o espaço de visão apropriado, a imagem é descrita
usando os autovetores de tal espaço de visão, e então
reconhece-o. Tem-se avaliado esta abordagem usando dados similares como
mostrado na Fig.5.
autoespaos separados, cada variação foi capturada de indivíduos
em uma visão comum. O autoespaço view-based é essencialmente
uma extensão da técnica autoface para múltiplos conjuntos
de autovetores, um para cada combinação de escala e orientação.
Alguém poderia pensar desta arquitetura como um conjunto pararelo
de observadores", cada um tentando explicar os dados da imagem com seu
conjunto de autovetores. Neste view-based, abordagem múltiplos-observadores,
o primeiro passo é determinar a localização e orientação
do objeto objetivo pela seleção do autoespao que melhor descreve
a imagem de entrada. Isto é efetuado pelo o cálculo do erro
descrição residual (a métrica distância-do-espaço-de-face")
usando cada um dos autovetores dos espaos de visão. Uma vez determinado
o espaço de visão apropriado, a imagem é descrita
usando os autovetores de tal espaço de visão, e então
reconhece-o. Tem-se avaliado esta abordagem usando dados similares como
mostrado na Fig.5.

Figura 5: Algumas da imagens usadas para testar a precisão do reconhecimento de face a despeito de amplas variações na orientação da cabeça. A precisão média de reconhecimento foi 92%, a orientação do erro teve um desvio padrão de 15o
Estes dados consistem de
189 imagens em nove visões de 21 pessoas. As nove visões
de cada pessoa foram igualmente espaçadas de a![]() diante de um plano horizontal. Os dados foram fornecidos por Westinghouse
Eletronic Systems. O desempenho de interpolação foi testado
pelo treinamento sobre um subconjunto de visões disponíveis
diante de um plano horizontal. Os dados foram fornecidos por Westinghouse
Eletronic Systems. O desempenho de interpolação foi testado
pelo treinamento sobre um subconjunto de visões disponíveis![]() e testando em visões intermediárias de
e testando em visões intermediárias de ![]() .
A média da taxa de reconhecimento obtido foi de 92%.
.
A média da taxa de reconhecimento obtido foi de 92%.
Reconhecimento Usando "AutoCaracterísticas"
Consiste do uso de características faciais para reconhecimento de face. Isto pode ser visto como uma representação modular ou por camadas da face, onde uma descrição grosseira (resolução baixa) de toda a cabeça é aumentada por detalhes adicionais (resolução alta) para salientar características da face. A técnica autoface foi extendida para detectar características faciais. Para cada característica da face, um espaço de características é construído pela seleção da maioria de autocaracterísticas significantes (autovetores correspondentes para grandes autovalores da matriz de correlação de características). Na representação autocaracterística a equivalente distância do espaço de característica" (DFFS) pode ser efetivamente usado para detecção de características faciais. A detecção de fatores DFFS foi extendida para detecção de características sob diferentes visões geométricas pelo uso ou de view-based autoespaço ou um autoespaço paramétrico [Nef96].Em [MP94] a técnica autoface é facilmente extendida para a descrição e codificação de características faciais, dando "eigeneyes", "eigennoses", "eigenmouths". Estudos do movimento do olhos indica que estas características faciais particulares represetam importante limite para fixação, especialmente em uma tarefa de discriminação. Então é esperado uma melhora no desempenho de reconhecimento pela incorporação de uma camada adicional de descrição em termos de características faciais. Isto pode ser visto como se uma representação modular ou em camadas de uma face, onde uma grosseira (baixa-resolução) descrição de toda a cabeça é aumentada por detalhes adicionais (alta-resolução) em termos de salientar características faciais. Com a habilidade para de forma confiante detectar características faciais através de uma larga escala de faces, pode-se automaticamente gerar uma representação modular de uma face. A utilidade desta representação em camada (autoface mais autocaracterísticas) foi testada em um pequeno subconjunto de sua base de dados de face. Selecionou-se uma amostra representativa de 45 indivíduos com duas vistas por pessoa, correspondendo a diferentes expressões faciais (neutro vs. sorridente). Este conjunto de imagem foi particionado entre um conjunto de treinamento (neutro) e um conjunto de teste (sorridente). Visto que a diferença nas expressões faciais é primeiramente articulada na boca, esta característica particular foi discartada para o propósito de reconhecimento. A Fig. 6 mostra as taxas de reconhecimento como uma função do número de autovetores para autoface-somente, autocaracterística-somente e a representação combinada.
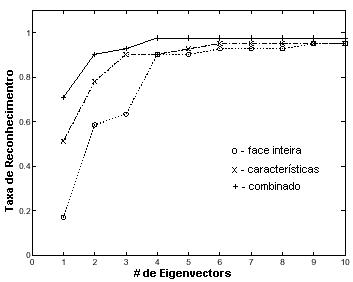
O que é surpreendente é que (para este pequeno conjunto de dados no mínimo) a autocaracterística sozinha foi suficiente para adquirir uma (assintótica) taxa de reconhecimento de 95% (igual para aqueles da autofaces). Mais surpreendente, às vezes, é a observação que em menores dimensões de autoespao, autocaracterística apresentam desempenho de melhor qualidade no reconhecimento autoface. Finalmente, pelo uso da representação combinada, ganha-se um leve melhoramento na taxa de reconhecimento assintótica (98%). A potencial vantagem da camada autocaracterística é a habilidade de superar as desvantagens de um método autoface padrão. Um puro reconhecimente autoface pode ser enganado por grosseiras variações na imagem de entrada (chapéus, barbas, etc.). Na Fig. 7(a) mostra visões testes adicionais de 3 indivíduos por cima de um conjunto de dados de 45 indivíduos. Estas imagens teste são indicativas do tipo de variação o qual pode conduzir a combinações falsas: uma mão próxima a face, uma pintura de face, e uma barba. A Fig. 7(b) mostra as combinações mais próximas encontradas baseada na classificação de padrão autoface. Nenhuma das 3 combinações correspondem ao indivíduo correto. Por outro lado, a Fig. 7(c) mostra a mais próxima combinação baseada nos olhos e nariz, e resulta na correta identificação em cada caso. Este simples exemplo ilustra a vantagem de uma representação modular na desambigüidade de combinações autofaces falsas.

Figura 7: (a) Visões
testes, (b) Autoface combinadas, (c) Autocaracterísticas combinadas
Método Discriminante Linear - Fisherfaces"
Neste novo método há a redução da dimensionalidade do espaço de características usando Discriminante Linear de Fisher (FLD) [21] apud [Nef96]. O FLD usa o classe de informação de um grupo e desenvolve um conjunto de vetores de características nos quais variações de diferentes faces são enfatizadas enquanto diferentes exemplos de faces combinadas com condições de iluminação, expressões faciais e orientação são desenfatizadas.Método Baseado no Modelo Markov Escondido
O Modelo Markov Escondido (HMM) é um conjunto de modelos estatísticos usados para caracterizar propriedades estatísticas de um sinal. HMM são feitos de dois processos interelacionados: (1)uma secreta não observável cadeia Markov com finitos números de estados, um estado de transição, matriz de probabilidade e um estado inicial, distribuição de probabilidade. (2)um conjunto de funções de densidade probabilidade associado a cada estado. Os elementos de uma HMM:-
N, o número de estados
no modelo. Se
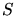 é o conjunto de estados, então
é o conjunto de estados, então 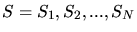 .
O estado do modelo no tempo
.
O estado do modelo no tempo 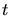 é dado por ,
é dado por , 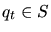 ,
, 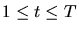 onde T é o tamanho da seqüência de observação
(número de frames).
onde T é o tamanho da seqüência de observação
(número de frames). -
M, o número de diferentes
símbolos de observação. Se V é o conjunto de
todas as observações de símbolos possíveis
(também chamado de modelo codebook), então,
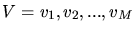
-
A, o estado de transição
matriz de probabilidade, i.e.
![\begin{displaymath}a_{ij}=P[q_{t}=S_{j}\vert q_{t-1}=S_{i}], 1 \leq i,j \leq N,\end{displaymath}](img51.png) onde
onde 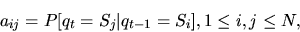
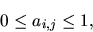
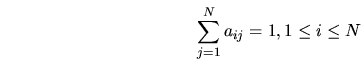
-
B, o símbolo de observação
da matriz de probabilidade, i.e.
![\begin{displaymath}b_{j}(k)= p[O_{t}=v_{k}\vert q_{t}=S_{j}], 1 \leq j \leq N, 1 \leq k\leq M\end{displaymath}](img55.png) ,
onde,
,
onde, -
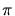 ,
distribuição de estado inicial, i.e.
,
distribuição de estado inicial, i.e. ![\begin{displaymath}\pi_{i}=P[q_{1}=S_{i}], 1 \leq i \leq N\end{displaymath}](img59.png) onde:
onde:
![]() e
e![]() é
o símbolo de observação no tempo t
é
o símbolo de observação no tempo t
.
- Usando uma notação
estenográfica, uma HMM é definida como:
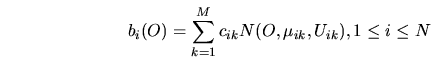
onde
HMM tem sido usado extensamente para reconhecimento de voz, onde os dados são naturalmente uni-dimensionais (1D) ao longo do eixo do tempo. Entretanto, o equivalente completamente conectado em duas dimensões HMM dominaria uma grande quantidade de problemas computacionais. Tentativas tem sido feitas para usar representações multi-modelos que conduzem ao um pseudo 2D HMM. Estes modelos são atualmente usados no reconhecimento de caracteres. Foi proposto em [Samaria et al] apud [Nef96] o uso de 1D contínuo HMM para reconhecimento de face. Assumindo que cada face está em uma posição ereta e frontal, características ocorrerão em uma ordem previsível, isto é, testa, olhos, nariz etc. Esta ordenação sugere o uso de um modelo top-bottom", onde somente transições entre estados adjacentes do modo de cima para baixo são permitidos. Os estados do modelo correspondem a características faciais como testa, olhos, nariz, boca e queixo. A sequência de observação O é gerada de uma imagem X x Y usando uma janela amostra X x L com X x M pixels sobrepostos (Fig. 8) [Nef96].
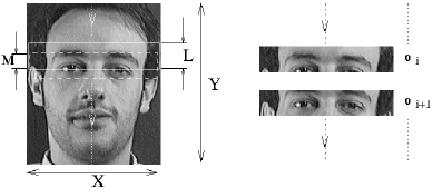
Cada vetor de observação
é um bloco de ![]() linhas. Há uma linha M sobreposta entre sucessivas observações.
A sobreposição permite que as características sejam
capturadas de uma maneira a qual é independente da posição
vertical, enquanto um particionamento disjunto da imagem poderia resultar
em características truncadas ocorrendo através das fronteiras
dos blocos. Desempenho do Reconhecimento: Neste trabalho, o desempenho
do reconhecimento foi testado em uma pequena base de dados de 50 imagens
que das quais não faziam parte da base de dados de treinamento 24
imagens [37] apud [Nef96]. As imagens do conjunto de teste contém
faces com diferentes expressões faciais, detalhes faciais (com ou
sem óculos) e variações na iluminação.
Nesta base de dados os autores relataram uma taxa de reconhecimento de
84%. No mesmo banco de dados a taxa de reconhecimento foi obtida pela execução
do método autoface foi de 73%. Entretanto, a computação
envolvida para o reconhecimento levou aproximadamente 12 segundos para
classificar uma imagem usando o conjunto de 24 modelos de treinamento,
em uma estação de trabalho SunSparc II.
linhas. Há uma linha M sobreposta entre sucessivas observações.
A sobreposição permite que as características sejam
capturadas de uma maneira a qual é independente da posição
vertical, enquanto um particionamento disjunto da imagem poderia resultar
em características truncadas ocorrendo através das fronteiras
dos blocos. Desempenho do Reconhecimento: Neste trabalho, o desempenho
do reconhecimento foi testado em uma pequena base de dados de 50 imagens
que das quais não faziam parte da base de dados de treinamento 24
imagens [37] apud [Nef96]. As imagens do conjunto de teste contém
faces com diferentes expressões faciais, detalhes faciais (com ou
sem óculos) e variações na iluminação.
Nesta base de dados os autores relataram uma taxa de reconhecimento de
84%. No mesmo banco de dados a taxa de reconhecimento foi obtida pela execução
do método autoface foi de 73%. Entretanto, a computação
envolvida para o reconhecimento levou aproximadamente 12 segundos para
classificar uma imagem usando o conjunto de 24 modelos de treinamento,
em uma estação de trabalho SunSparc II.
Misturas de Subespaços Linear Local
No trabalho de [BJF98] temos a análise de desempenho de reconhecimento de um modelo de misturas de subespaços linear local que pode ser combinado para treinamento dos dados usando algoritmo de maximização de expectativa. O modelo misturado tem melhor desempenho do que um classificador vizinho mais próximo" operando em um subespaco PCA (análise de componente principal) ou expansão Karhunen-Loeve. Foi mostrado o quanto esta abordagem de reconhecimento é robusta para modelagens de faces como na Fig. 9. Em uma abordagem para visualizar a modelagem da face, imagens de face N-pixel normalizadas são projetadas sobre um subconjunto de D autovetores ou autofaces de matriz de covariância estimada do conjunto de treinamento de imagens. O subespaço D-dimensional atravessado por estas autofaces ortogonais é o subespaço no qual os dados de treinamento tem a maior variação. De fato, estas autofaces são iguais aos primeiros D principais componentes obtidos da análise de componente principal. A distância de uma nova imagem de entrada deste subespaço linear tem sido usada totalmente com sucesso para detectar faces. Foi considerado que uma mistura de K subespaços linear como uma mistura de K analizadores de fator, onde cada analizador de fator tem o mesmo número D de fatores. Sejaonde
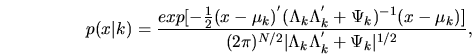 Após
isto ser computado deve-se obter então
Após
isto ser computado deve-se obter então ![]() .Se
dado um modelo de mistura para cada classe de dados (por exemplo, indivíduo
para ser reconhecido), isto procederá dando
.Se
dado um modelo de mistura para cada classe de dados (por exemplo, indivíduo
para ser reconhecido), isto procederá dando ![]() para
diferentes classes
para
diferentes classes ![]() .
Aplica-se então a regra de Bayes para fazer a decisão do
reconhecimento.
.
Aplica-se então a regra de Bayes para fazer a decisão do
reconhecimento.
No processo de compilação
de uma base de dados de seqûëncias de vídeo de um número
relativamente pequeno de indivíduos (100), mas com alta variação
nas expressões faciais e poses, tais como na Fig. 9, que mostra
algumas das imagens de vídeo mais testadas da base de dados. Esta
aplicação mostrou-se altamente robusta para o reconhecimento
de face em ambientes fechados como uma área de escritório.

Figura 9: Exemplos de formas de vídeo e faces normalizadas.
Abordagem Estatística para a Detecção de Faces
O trabalho de [MHY99] mostra que a interação humano computador tem se tornado uma ativa área de pesquisa em que interfaces mais amigáveis e efetivas vem sendo desenvolvidas. Entre todas as interface humano computador, é mais comum acreditar que faces humanas é um dos mais efetivos meios, visto que ela carrega enormes informações as quais computadores podem reagir de acordo. Por exemplos, computadores podem ajustar seu comportamento pelo conhecimento das emoções do usuário, através de suas expressões faciais. Atenção visual é outro exemplo onde computadores podem reagir baseados nos interesses de seus usuários. Em direção a este objetivo, reconhecimento de face e expressão facial tem atraído muita atenção recentemente e embora já venha sido estudada a mais de vinte anos por psicólogos, neurocientistas e engenheiros. Muitas aplicações interessantes e úteis tem sido desenvolvidas com estes esforços. A maioria dos métodos existentes assumem que faces humanas devem ser extraídas de imagem estática ou de uma seqüência de imagens e focalizar algoritmos de reconhecimento. Entretanto, detecção de face de uma imagem simples ou uma seqüência de imagens é uma tarefa muito desafiante e não mais fácil do que reconhecimento de face. Detecção de face é consideravelmente difícil porque envolve localização de face com nenhum conhecimento prévio de sobre suas escalas, localizações, orientações(ereta, rotacionada) com ou sem oclusões, com diferentes posições (frontal, perfil). Expressões faciais e condições de iluminação também alteram por completo aparências de faces, tornando-se difícil detectá-las. Além disto, a aparência de faces humanas em uma imagem depende da posição de humanos e de visões dos dispositivos de aquisição. Os desafios associados com problemas de detecção de face podem ser atribuídos aos seguintes fatores:- Posições: Faces podem aparecer em diferentes posições (frontal, ângulo de 45 graus, perfil, parte superior inclinada para baixo) o que faz suas aparências variar nas imagens. Algumas posições podem ocluir características faciais tal como olhos e nariz.
- Presença ou ausência de características estruturais comuns: Faces humanas fazem diferentes características faciais tais como barba, bigode ou óculos. Além disso, tais características tem diferenças drásticas na aparência por causa da localização e tamanho.
- Expressões faciais: A aparência de faces humanas são afetadas por suas expressões faciais.
- Oclusões: Faces podem ser ocluídas por outros objetos. Em uma imagem com um grupo de pessoas, algumas faces podem parcialmente ocluir outras faces.
- Condições de formulação da imagem: fatores de imagem afetam o resultado da aparência de faces humanas quando a imagem é formulada, através de problemas causados tais como escala, orientação, visão, e condições de iluminação.
Abordagem Autoface
Um método de aprendizagem visual probabilístico, baseado na estimação da densidade em um espaço altamente dimensionado usando decomposição de autoespaço, foi desenvolvido por Mogaddam e Pentland [1] apud [MHY99]. Na análise de componente principal, os maiores autovalores e autovetores são identificados e selecionados como componentes principais para formar um subespaço. Estes componentes principais preservam as principais correlações lineares nos dados e discartam as sem importância. Em contraste, tem-se a forma de uma decomposição ortogonal do espaço vetor dentro de dois subespaços mutuamente exclusivos e complementares: o principal subespaço (ou espaço de características) e seus complementos ortogonais. Então, a densidade objetivo é decomposta em dois componentes: a densidade em um subespaço principal (transposto por componentes principais) e seus complementos ortogonais (os quais são discartados na análise de componente principal padrão). A multivariável Gaussian e uma mistura de variáveis Gaussians são usadas para aprender as características estatísticas de características locais de uma face. Estas densidades probabilidades são então usadas para detecção de objeto basedas em uma estimação de probabilidade máxima. O método proposto tem sido aplicado para localização de face, codificação e reconhecimento. Comparada com a clássica abordagem autoface, o método proposto mostra melhor desempenho no reconhecimento de face. Em termos de detecção de face, suas técnicas tem sido somente demonstradas na localização (isto é, assumindo que uma imagem de entrada possui somente uma face).Abordagem Probabilística
Em [52] apud [MHY99] Schneiderman e Kanade descrevem um modelo probabilístico para reconhecimento de objeto basedo primeiramente na aparência do local, o qual difere significativamente da aparência baseada no método que enfatiza a aparência global. Esta abordagem é comparada a métodos nos quais modela o todo, extensão global do objeto, e neste caso a face humana, junto. A razão deles enfatizarem a aparência local é que alguns padrões locais no objeto são mais únicos do que outros. Para faces humanas, os padrões de intensidade ao redor dos olhos de uma face humana são mais exclusivos do que o padrão encontrado nas bochechas. Para representar a aparência exclusiva do local, aparências estatísticas e local necessitam ser modeladas. A razão delas usarem uma forma funcional de função de probabilidade posterior é capturar a junção estatística da aparência local e posição no objeto bem como as estatísticas da aparência local. Este modelo probabilístico de relacionamento entre aparência local e spacial mostra desempenho comparável com a detecção de face baseadas em redes neurais. Em [53] apud [MHY99] uma alta ordem estatística baseada em algoritmos de clusterização e um molelo Markov escondido, esquema (HMM) são propostos para detecção de face. No primeiro método, a distribuição desconhecida da face e face com cópia são modeladas usando alta ordem estatística. A conjectura é que a distribuição de diferentes padrões face deve ser governada por funções Gaussian multidimensionais. Um perceptron multicamada é usado para classificação, em [45] apud [MHY99]. O segundo método usa uma HMM para aprender entre face e não face e transições de face e não face. A sequência de observação é gerada no domínio de transformação pela comparação de cada subimagem máscara com uma base de conhecimento consistindo de 6 faces e 6 faces como centróides, similar a métrica de distância usada em [45] apud [MHY99].Exemplo de Ferramenta de Detecção de Face com Técnicas Estatísticas
A seguir é apresentado uma ferramenta desenvolvida por [Vis98] usando técnicas estatísticas (Autofaces e Pirâmide de Gaussian) para a detecção de face.- Objetivo
- Considerações
- Algoritmo
- Imagens de Saída
- Desempenho
- Problemas e Críticas Apresentadas
- Implementação
Objetivo
O objetivo da ferramenta
é detectar faces de diferentes tamanhos em imagens em escala de
cinza. O programa
desenha um contorno quadrado
ao redor da posição na imagem de entrada onde a probabilidade
de se encontrar
uma face é máxima.
Considerações
- Há exatamente uma face na imagem de entrada.
- As faces aparecem aproximadamente em visões frontais.
As faces não são inclinadas ou rotacionada na imagem.
Algoritmo
- O algoritmo usado para a
detecção de face foi baseado em uma sugestão de Moghaddam
e Pentland (1997)
Determinações
-
Foram determinadas 42 autofaces
e autovalores e a face média, i.e.,
 .
.
Foram determinados códigos MATLAB para geração de pirâmides.
Passos de Pré-Processamento
- A face média e cada uma das autofaces são cortadas até que somente as partes não zero sejam retidas. Isto poupa a computação sem afetar o resultado pela rejeição dos zeros que cercam as imagens.
- A imagem de entrada é escalada por (3/4) na direção x afim fazer a relação largura e altura da entrada iguais as das imagens usadas no conjunto de treinamento, para geração das autofaces.
Parâmetros
Os valores dos parâmetros foram mantidos para todas as imagens mostradas.- M, o número de autofaces usadas para a detecção de face, M=20.
-
Rho, o multiplicador que determina
o peso da distância dos espaços de características
(DFFS) relativa a distância do espaço de fatores (DIFS). Para
esta simulação mostra-se:
 .
. - O número de níveis capaz de construir a imagem de entrada.
Algoritmo
- Uma quarta-oitava pirâmide de Laplace é construída pela junção de todas as 4 pirâmides oitavas completas gerada pela imagem de entrada e escaladas abaixo da versão delas.
- A cada escala desta pirâmide, uma janela de entrada de mesmo tamanho da face média aparada é correlacionada com a face média aparada. Antes da correlação, se a entrada inteira para esta escala ou a janela de entrada são normalizadas assim que elas obtém a mesma iluminação e variância média como a face média aparada.
- A cada escala da pirâmide e cada janela de entrada, a distância Mahalanobis é computada adicionando a distância no espaço de características (DIFS) e a distância do espaço de características (DFFS). Em alguns casos, melhores desempenhos são obtidos usando somente DIFS e ignorando DFFS.
- A janela de entrada é então deslocada ao redor de todas as partes da imagem de entrada na escala atual da pirâmide e os cálculos acima são repetidos.
A posição da mínima distância de Mahalanobis que cruza todas as escalas e posições na janela de entrada é encontrada. Esta é a posição e a escala onde a probabilidade de se encontrar uma face na imagem é máxima.
Imagens de Saída
As seguintes imagens foram obtidas tanto pelo uso da distância DFFS como da DIFS: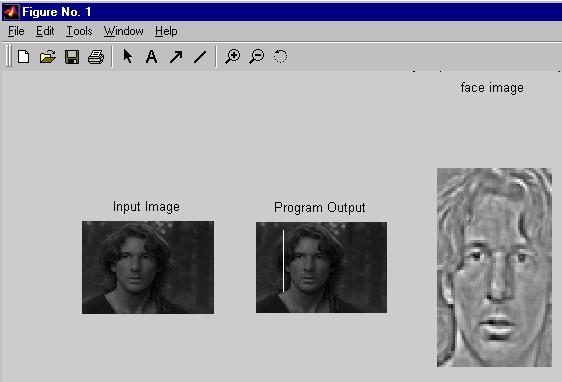
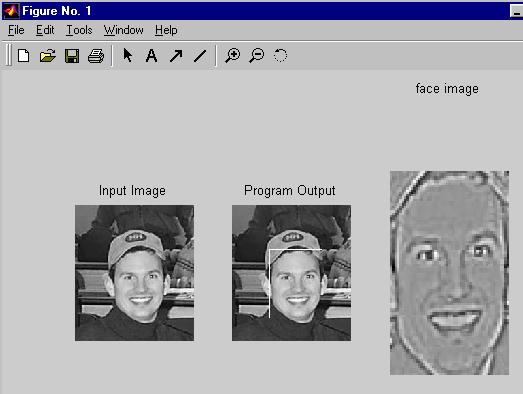
Imagem obtida usando somente a distância DIFS e ignorando DFFS:
Imagens onde o programa falha:
Figura:14
Desempenho
O programa tem sucesso no encontro de 8 das 10 faces segundo demonstrado em [Vis98]. Interessantemente, em uma das imagens onde ela falha, ele parece preferir uma face de lado, parcialmente ocluída ao fundo com relação à face que está de frente, veja Fig.14. Este problema pode ser resolvido usando mais níveis na pirâmide Laplaciana da entrada.Problemas e Críticas Apresentadas
- A abordagem autoface para reconhecimento de face essencialmente amarra a imagem de entrada ao conjunto de treinamento dentro de um vetor e computa os autovalores e autovetores deste conjunto de vetores. Isto não faz qualquer utilidade no uso de propriedades geométricas das mesmas faces, tais como a localização dos olhos, com relação ao nariz e a outras características faciais. Isto faz a abordagem ser geral em que se possa classificar e reconhecer qualquer tipo de objeto baseada nas imagens de treinamento. Ao mesmo tempo, isto lança muitas informações sobre características faciais. Isto também faz o método ser altamente improvável de se parecer com maneira como os humanos reconhecem faces. O sucesso do algoritmo depende largamente da generalização do conjunto de treinamento usado para gerar as autofaces.
- Este algoritmo não pode detectar faces que são muito menores do que a face média. Este problema pode ser resolvido pela construção de pirâmides para as autofaces, a face média e a entrada. Entretanto, isto aumenta enormemente o número de cálculos. Enquanto se faz isto, deve-se ter o cuidado com a escala de uma autoface por um fator de (1/m) acompanhada por uma escala de autovalores correspondentes por um fator de (1/m)2.
- O desempenho é autamente dependente da largura x altura nas imagens de entrada.
Na maioria dos casos, o uso de DFFS melhora o desempenho, mas em alguns, ele atrasa o desempenho. A escolha de usar ou não usar a distância DFFS se dá pela experiência.
Implementação
Esta ferramenta de detecção de face foi programada em MATLAB 5.2 usando a caixa de ferramentas de processamento de imagem. O código desta aplicação foi dividido nos seguintes arquivos:- face.m: Programa principal. Este arquivo detecta a face na imagem de entrada.
- makeImPyr.m: Função que constrói uma pirâmide Laplaciana quarta-oitava pela junção de quatro pirâmides oitavas completas, geradas das versões de escalas da entrada.
- plot_eigen.m: função que esboça a face média aparada e autofaces.
- suptitle.m: Código obtido da página da MATHWORKS para colocar um título sobre todas subimagens em uma figura (escrito por Drea Thomas, drea@mathworks.com)
- matlabPyrTools.tar.gz: Código fonte com ferramentas de pirâmide MATLAB (do departamento CIS da Universidade da Pensilvânia )
- average_face.mat (131Kb)
- eigenfaces.mat (5.5 Mb)
- eigenvalues.mat
showme.m
Conclusão
Este trabalho teve como objetivo apresentar um estudo sobre reconhecimento de padrões estatístico e mostror vários exemplos de abordagens estatísticas empregadas no reconhecimento de faces humanas. Dentre as várias abordagens vistas, temos que o método de correlação atua com alta precisão, se iluminação artificial e normalização do tamanho são aplicadas, sob variações na expressão facial e posições. Entretanto, este método é computacionalmente muito complexo. A mais eficiente abordagem para o reconhecimento de face é o método autoface. Embora o desempenho de reconhecimento é menor do que o método de correlação, a redução substancial na complexidade do método autoface faz este método ser mais atrativo. A taxa de reconhecimento aumenta com o número de componentes principais usados (autofaces) e quanto mais componentes principais são usados, o desempenho aproxima-se do da correlação. Vimos que por meio da abordagem paramétrica, onde os parâmetros são conhecidos eou estimados, extende-se a capacidade do método Autoface para reconhecimento de objetos em imagens 3D, fazendo com que um espaço paramétrico descreva a identificação de um objeto visulização e iluminação. A partir da decomposição deste espaço desenvolveu-se uma abordagem em autoespaço chamada "view-based" que se realiza sob condição gerais de visão, para o reconhecimento de face. No reconhecimento de faces usando autocaracterísticas são utilizadas características faciais gerando uma representação modular da face e sua potencial vatagem é a habilidade de superar as desvantagens do método autoface padrão, que pode ser facilmente enganado por grosseiras variações na imagem de entrada (chapéu, barbas, etc). O método de discriminante linear de Fisher é proposto para reduzir a dimensionalidade do espaço de características, como exemplos teve-se os trabalhos de [19] e [20] apud [Nef96] nos quais tratam respectivamente, Autofaces x Fisherfaces no reconhecimento usando classes específicas de projeções lineares e reconhecimento de faces usando discriminantes autovetores. Já o método baseado em HMM o qual é bem sucedido no reconhecimente de voz, mostrou que é significantemente melhor para o reconhecimento de face do que o método Autoface. Istó é devido ao fato de que o método baseado em HMM oferece uma solução para detecção de características faciais bem como reconhecimento de face. Entretanto a 1D HMM contínuas são computacionalmente mais complexas do que o método Autoface. A solução é reduzir o tempo de execução deste método com o uso de HMM discreta. Foi apresentado também um método que reune misturas de subespaços linear local, que tem melhor e mais robusto desempenho do que o classificador "vizinho mais próximo" operando em um subespaço de análise componente principal ou expansão Karhunen-Loeve. Foi apresentado também um breve estudo sobre métodos de detecção de face com abordagens estatísticas, e para que um sistema de detecção de face seja robusto, projetistas devem-se preocupar com os seguintes problemas: utilização de mistura de diferentes classificadores, efeitos das condições de iluminação, detecção da face em diferentes posições, experimentos empíricos para comparações e uma base de bados para "bechmarking". Recentemente muitas abordagens estatísticas usam uma mistura Gaussian ou uma mistura de subespaços para reconhecimento de faces humanas. O problema é que face humana é algo que não pode ser propriamente representado por um padrão simples "cluster". Além do mais, a maioria dos sistemas de detecção usam face com expressões neutras e pouco características faciais. Para se construir um sistema de detecção que possa identificar faces, é natural esperar que diferentes clusters sejam melhor representados por diferentes subespaços. Deteção de face é um problema muito desafiante e interessante, e portanto é o primeiro passo prático e importante para se construir um completo sistema de reconhecimento de face automático. E como há um enorme e crescente interesse nas interações humano-computador, é importante investigar métodos que possam ter desempenhos cada vez mais rápidos e robustos.
Bibliografia
Contato:
Tel.: +55-48-331 7552/9498 |



