
Visão Computacional
1. Representação de
imagens
2. Filtragem de imagens
3. Detecção de Bordas
4. Segmentação Simples
5. Crescimento de Regiões
6. Segmentação com
Filtros
7. Segmentação a Cores
8. Análise de Texturas
9. Análise de Texturas
Multiescalar
10. Redes Neurais
11. Morfologia Matemática
12. Convolução
13. Esqueletonização
14. Técnicas Estatísticas
15. Fractais
16. Reconhecimento de
Formas
17. Representação de
Objetos
18. Quadtrees e Octrees
19. Visão Estereo
20. Inteligência Artificial
21. Controle de qualidade
22. Robótica
23. Medicina
24. Sensoriamento remoto
Prof. Aldo von Wangenheim
Currículo...
Publicações
Pesquisa
Projetos
Ensino de Graduação
Ensino de Pós Graduação
Cursos
A Linha Essencial
José Alexandre de França
Introdução
Quando os computadores tornaram possível o reconhecimento de padrões, foi preciso reduzir a quantidade de informação a ser processada ao mínimo necessário. Os trabalhos pioneiros neste sentido foram concentrados sobre padrões de caracteres já na década de 50. Em [37], foi descoberto que uma operação de média sobre uma janela quadrada com um limiar (threshold) elevado resulta no afinamento (thinning) da imagem de entrada, e em [61], uma operação chamada "custer operation" foi utilizada para obter-se o esqueleto de certos padrões de caracteres. Após isto, diversos pesquisadores como [107], [32], e [2], utilizaram algoritmos de esqueletonização para reconhecimento de caracteres. Desde então, essa técnica é muito utilizada e até circuitos integrados têm sido projetados para esse propósito.
Durante os últimos anos, diversos algoritmos de compressão de dados baseados na esqueletonização foram propostos e aplicados a uma grande variedade de padrões para diferentes propósitos. Na década de 60, descobriu-se que essa técnica é útil no campo da biomédica, quando um algoritmo de encolhimento (shrink) foi aplicado para contar e medir as partes constituintes dos glóbulos brancos a fim de identificar células anormais [58], [94]. Desde então, aplicações nesta área incluem análises de células brancas do sangue e cromossomos, análise automática de imagens de raio-X e artérias coronárias. Em outros setores, a esqueletonização tem sido empregada em sistemas de visão de autônomos, classificação de impressões digitais, padrões de rachaduras, análise visual automática de partes industriais, placas de circuitos impressos, dentre outros.
Esta grande variedade de aplicações mostra a aplicabilidade de reduzir-se padrões a uma fina linha representativa. Isto, por sua vez, pode ser atribuído à necessidade de reduzir a quantidade de dados, bem como o fato de que a análise de formas pode ser feita mais facilmente sobre padrões de esqueletos. Além disso, a representação através de esqueletos de certos padrões, por exemplo, caracteres, pode ser mais próximo do conceito humano desses padrões. Portanto, eles favorecem uma análise estrutural simples e um projeto mais intuitivo de algoritmos de reconhecimento. Adicionalmente, a redução de uma imagem a sua essência pode eliminar algumas distorções no contorno enquanto mantém as propriedades geométricas e topológicas. Em termos mais práticos, a esqueletonização pode fornecer uma representação mais fácil de extrair-se propriedades críticas como pontos extremos, junções, e conexões ao longo dos objetos em uma imagem, considerando que algoritmos de vetorização (sempre usados em tarefas de reconhecimento de padrões) sempre requerem linhas de entrada de um pixel de largura.
Naturalmente, para um algoritmo de esqueletonização ser eficiente, ele precisa idealmente compactar dados, manter propriedades significativas dos padrões, e eliminar ruídos locais sem introduzir distorções. Conseguir todas essas proezas usando um algoritmo simples e rápido é um desafio.
- Definições
- Tipos de Algoritmos
O termo esqueleto é geralmente utilizado
para denotar uma representação de um padrão através
de uma coleção de arcos e curvas finas. Alguns autores usam
termos diferentes, por exemplo, "eixo médio" (medial axis)
[101] e "thinned image" [este]. Contudo, "thinning" e "esqueletonização"
tornaram-se os mais utilizados na literatura. Além disso, o termo
"esqueleto" é utilizado para referir-se ao resultado do algoritmo.
Nesta seção, são apresentados aspectos gerais presentes nos diversos algoritmos de esqueletonização, ou, mais precisamente, nos algoritmos que excluem de forma sucessiva diversas camadas da extremidade (borda) de um padrão até que apenas um esqueleto permanece. A exclusão de um ponto p dependerá dos pixels na vizinhança deste ponto. De acordo com o modo de como se examinam os pixels, estes algoritmos podem ser classificados como seqüenciais ou paralelos. Nos algoritmos seqüenciais, os pixels são examinados para exclusão em uma seqüência fixa em cada interação, e a exclusão de p na n-ésima interação depende de todas as operações que tenham sido realizadas até aquele momento, isto é, do resultado da (n-1)-ésima interação, bem como dos pixels já processados na n-ésima interação. Por outro lado, nos algoritmos paralelos, a exclusão na n-ésima interação depende apenas dos pixels da interação n-1. Por isso, todos os pixels podem ser analisados independentemente de forma paralela a cada interação.
É importante notar que a divisão dos algoritmos de esqueletonização em seqüenciais e paralelos é uma classificação bastante simplificada, pois, mesmo algoritmos que pertencem a uma mesma classe (seqüencial ou paralela) podem ser muito diferentes. De uma forma geral, a diferença maior está nos testes implementados para garantir a conectividade. Estes testes utilizam definições como "número de cruzamentos", "número de conexões" e "simplicidade de pixel" (pixel simplicity), na tentativa de garantir a conservação das formar geométricas e topológicas dos padrões processados.
A seguir, são definidas propriedades que são usadas durante o restante deste trabalho.
Definição 1: Uma imagem é o conjunto de todos os pontos no Plano Euclidiano. Um conjunto é finito se contém apenas um número finito de elementos. Considere S como sendo uma imagem finita e B = {0, 1}. Uma imagem binária finita é uma função V que mapeia S em B. Logo, a imagem binária é unicamente definida pelo seu conjunto de pontos de primeiro plano (ou pixels pretos), P. Além disso, complemento do conjunto P é chamado de conjunto de pontos de fundo (ou pixels brancos).
P = { p | p Î S Ù V(p) = 1}
Definição 2: N(p1) é o conjunto de todos os vizinhos de p1 e chamado de neighborhood de p1 (Figura 1). Os vizinhos com índices pares (p2, p4, p6 e p8 ou norte(p), leste(p), sul(p) e oeste(p)) são 4-neighbors de p1; os vizinhos com índices ímpares (p3, p5, p7 e p9 ou nordeste(p1), sudeste(p1), sudoeste(p1) e noroeste(p1)) e mais os 4-neighbors são chamados 8-neighbors de p1.
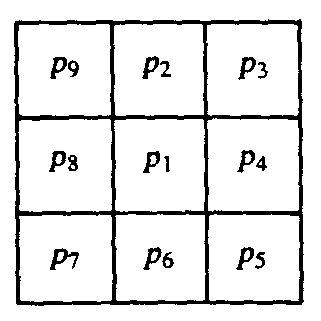
Figura 1 – Vizinhança de um ponto p1 utilizado em algoritmos de esqueletonização.
Definição 3: Peso de p (weight number de p), WN1(p), é definido como:
WN1(p) = ![]() .
.
Para uma janela 3x3, os pesos dos pixels estão entre 0 e 255. O conjunto que consiste de todos os pesos é chamado WS = {0, 1, ..., 255}.
Definição 4: Número de vizinhos (neighbor number) de p, NN(p), é o número de vizinhos diferentes de zero do ponto p.
Definição 5: Número de transições (crossing number) de p1, CRN(p1), é o número de transições de 0 para 1 na seqüência de p2, p3, ..., p9, p2.
Definição 6: Um ponto, p em P, é um ponto extremo (end point) se NN(p) = 1. Todos os pontos extremos pertencem ao conjunto chamado ES.
Definição 7: Número de conexões (connection number) de p, CN(p), é definido como:
CN(p) = ![]()
Note que ![]() - 1 = p[k] e p[8] = p[0].
- 1 = p[k] e p[8] = p[0].
Definição 8: Um ponto, p em P, é chamado removível globalmente (globally removable) se CN(p) = 1 e NN(p) > 1. Todo ponto globalmente removível pertence ao conjunto chamado GRS.
Definição 9: Um ponto, p em P, é chamado irreduzível (irreducible) se p não é globalmente removível. Todo ponto irreduzível pertence a um conjunto chamado IPS. IPS = WS – GRS.
Definição 10: Conjunto localmente removível (locally removable set), LRS, é um subconjunto de GRS e, nos algoritmos de esqueletonização paralelos, é definido por subinteração. Um ponto p em LRS é chamado ponto removível e os seus vizinhos que estão em LRS são chamados vizinhos removíveis. Nas subinterações dos algoritmos paralelos, definem-se conjuntos LRS. Por exemplo, em 4-subinterações, define-se quatro conjuntos localmente removíveis: LRS4[1] = {p | p em GRS e norte(p) = 0}, LRS4[2] = {p | p em GRS e sul(p) = 0}, LRS4[3] = {p | p em GRS e leste(p) = 0} e LRS4[4] = {p | p em GRS e oeste(p) = 0}.
Definição 10: Um esqueleto S é dito ser um-pixel-de-largura (one-pixel-wide) se todos os pontos em S pertencem a IPS.
Como já foi dito, dois grandes grupos
nos quais se classificam os algoritmos de esqueletonização
são: os algoritmos seqüenciais e os paralelos. Algoritmos seqüenciais
geram esqueletos melhores (do ponto de vista da conectividade e da conservação
da topologia). Contudo, exigem muito tempo de processamento. Já
os algoritmos seqüenciais, caracterizam-se pela velocidade, mas muitas
vezes originam esqueletos com falhas. Além desses dois grupos, há
ainda um terceiro que se caracteriza por (tentar) gerar o esqueleto em
apenas um passo de processamento. São os chamados algoritmos não-interativos.
Nas próximas seções, esses métodos são
analisados em detalhe.
A seguir, apresenta-se o algoritmo MAT para imagens binárias Para isto, assume-se que pontos da imagem têm o valor 1 e pontos do fundo têm o valor 0 (zero).
O método consiste de sucessivas aplicações ao contorno da imagem de duas regras básicas, onde pontos do contorno são quaisquer pontos com o valor 1 e que tenha ao menos um dos seus oito vizinhos iguais a 0 (Figura 1).
A primeira regra a ser aplicada a região define que um ponto p1 é marcado para exclusão se todas as quatro condições a seguir são satisfeitas:
- 2 £ NN(p1) £ 6;
- CRN(p1) = 1;
- p2 · p4 · p6 = 0;
- p4 · p6 · p8 = 0;
(c’) p2 · p4 · p8 = 0;
(d’) p2 · p6 · p8 = 0;
O passo 1 é aplicado a todo ponto da borda da região considerada. Se uma ou mais condições (a) – (d) são violadas, o valor do ponto em questão não é mudado. Se todas as condições são satisfeitas o ponto é marcado para exclusão. Contudo, os pontos não são excluídos até todos os pontos da borda terem sido processados. Isto previne mudanças na estrutura dos dados durante o processamento. Após o passo 1 ter sido aplicado em todos os pontos, aqueles que foram marcados são excluídos (tornados igual a 0). Então, o passo 2 é aplicado a imagem da mesma forma que o passo 1.
Resumindo, uma interação do algoritmo de afinamento consiste de (1) aplicar o passo 1 para marcar os pontos da borda para exclusão; (2) excluir os pontos marcados; (3) aplicar o passo 2 para marcar os pontos da borda para exclusão; e (4) excluir os pontos marcados. Este procedimento é aplicado interativamente até que nenhum ponto seja excluído. Quando o algoritmo terminar, o esqueleto da região estará originando.

Como dito anteriormente, existem diversos trabalhos que apresentam novos algoritmos de esqueletonização que podem ser classificados como seqüenciais. Exemplos podem ser encontrados em [10], [130], [47] e [52]. Em particular, o algoritmo proposto por [52] foi ampliado por [82] e utiliza uma janela de vizinhança de k x k (k ³ 3), na qual o centro (core) de (k – 2) x (k –2) pixels pode ser excluído. Evidentemente, com valores de elevados k, pode-se excluir grandes camadas de pixels em apenas uma interação. Com isso, apenas poucas interações são necessárias para obter-se esqueletos. Contudo, este aumento de velocidade é conseguido ao custo de qualidade, ou seja, obtém-se esqueletos com um certo grau de ruído.
- Algoritmos Paralelos
- Métodos Não-Interativos
Na esqueletonização paralela,
os pixels são examinados para exclusão baseados apenas
na interação anterior. Por esta razão, estes algoritmos
são indicados para implementação em computadores paralelos.
Dessa forma, os pixels que satisfazem a determinadas condições
podem ser excluídos ao mesmo tempo. Infelizmente, algoritmos completamente
paralelos podem ter dificuldades em conservar a conectividade das imagens.
Por exemplo, um retângulo horizontal com dois pixels de largura
pode desaparecer completamente em tais algoritmos [este]. Por isso, uma
prática usual é usar uma vizinhança de 3 x 3, mas
dividir cada interação em subinterações ou
subciclos, nos quais apenas um subconjunto dos pixels do contorno
são considerados para remoção. Ao fim de cada subinteração,
a imagem remanescente é atualizada para a próxima subinteração.
Quatro subciclos têm sido utilizados, nos quais cada tipo de ponto
do contorno (norte, leste, sul, e oeste) é removido a cada subciclo
[115], [101], [17]. Outra abordagem é utilizar apenas duas subinterações
[115], [136], [21], [118], [49] com, por exemplo, uma subinteração
excluindo os pontos norte e leste do contorno e outra excluindo o restante.
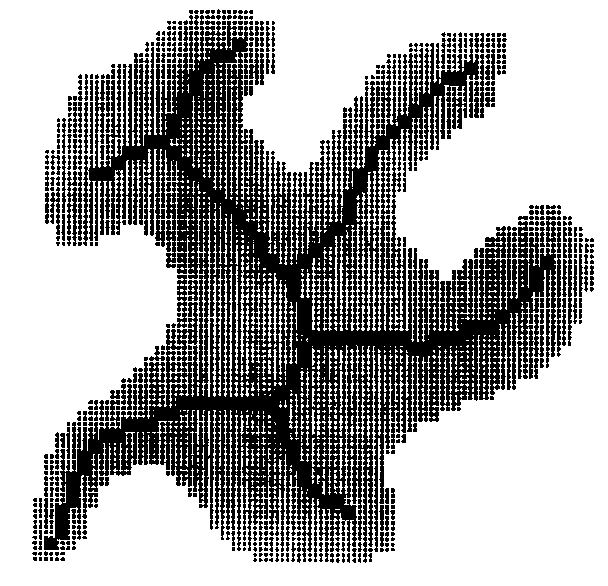
Esqueleto conseguindo com o algoritmo paralelo proposto por [1].
O algoritmo de Zhang e Suen é composto por duas subinterações. Na primeira subinteração, p é excluído se satisfaz as condições seguintes:
Z1: 2 £ NN(p1) £ 6;
Z2: CRN(p1) = 2;
Z3: p2 · p4 · p6 = 0;
Z4: p4 · p6 · p8 = 0.
Na Segunda subinteração, Z3 e Z4 são substituídas por suas rotações de 1800. Portanto, o primeiro subciclo exclui 4 pixels nas bordas sul, leste e noroeste, já o segundo exclui pixels nas posições opostas a do primeiro. Apesar da simplicidade, este algoritmo é imune a ruídos de contorno. Infelizmente, ele não gera esqueletos de um pixel de largura, linhas diagonais de dois pixels de largura podem ser seriamente erudidas e quadrados de 2x2 são completamente eliminados do esqueleto. Para evitar estes problemas, mais tarde, propôs-se que a condição Z1 fosse mudada para 3 £ NN(p1) £ 6. Contudo, essa solução cria o problema de reter outros pixels deveriam ser extraídos.
Concluindo, pode parecer que, em oposição aos algoritmos seqüenciais, muita da complexidade dos algoritmos paralelos resulta da necessidade de preservar a conectividade entre operações paralelas em uma pequena vizinhança da imagem. Este é um problema particular da natureza paralela do algoritmo de esqueletonização.
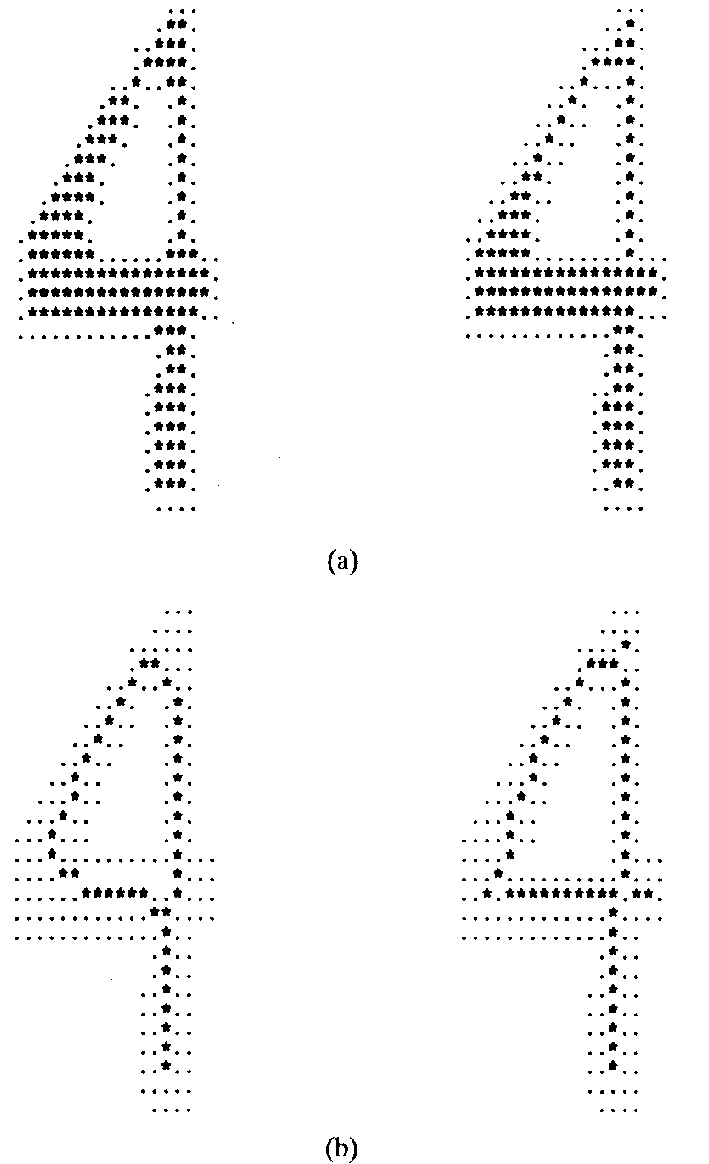
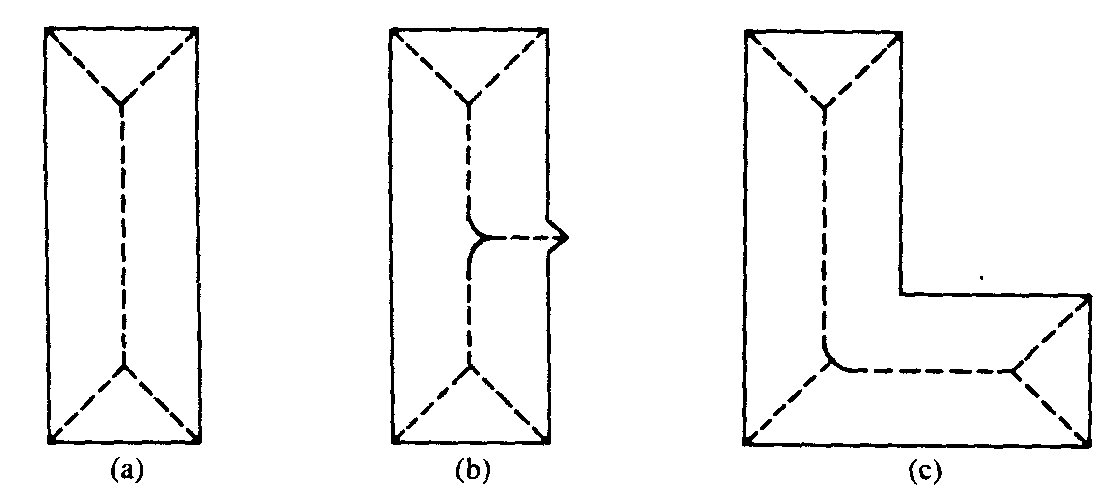
Figura 5 – Esqueletonizaçãoo por algoritmos paralelos e seqüenciais [53]: (a) após um ciclo; (b) resultado final. A figura da esquerda em (a) e (b) mostra resultados do algoritmo paralelo (4 ciclos), e as da direita montra os do seqüencial (três ciclos).
A categoria mais simples destes algoritmos determina os pontos médios, ao longo de uma linha de varredura, de pequenas regiões que fazem parte do padrão contido em uma imagem. Mas explicitamente, o algoritmo pode ser descrito da forma a seguir.
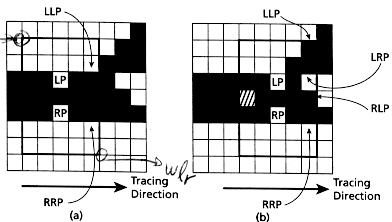
- Escolhe-se um ponto à esquerda, LP (Fig.???), e um à direita, RP (Fig.??), na borda do padrão e constrói -se uma janela com distância fixa a partir de LP até RP.
- O pixel central entre LP e RP faz parte do esqueleto.
- Localizam-se os pontos LLP e RRP (Fig.???) na borda da janela na direção de varredura do esqueleto.
- Desloca-se a janela para o novo ponto (LP = LLP e RP = RRP).
- Quando um pixel de fundo é encontrado dentro da janela, existe uma ramificação.
- Seleciona-se, na borda da janela, o pixel anterior entre LLP e RRP como LRP e o pixel posterior ao pixel de fundo como RLP.
- Recursivamente, faz-se LP = LLP e RP = LRP.
- Ao retornar-se, faz-se LP = RLP e RP = RRP (do ponto ramificado).
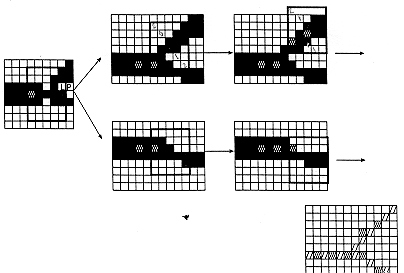
(c)
A Fig.??? mostra o esqueleto resultante de um algoritmo não-interativo. (Os pixels esqueletais estão conetados com linhas finas para facilitar a visualização.) Como pode-se observar, apesar da vantagem de serem métodos computacionais eficientes, eles criam desconexões quando os padrões processados possuem strokes muito paralelos as linhas de rastreamento [87]. Por isso, eles devem apenas ser usados em casos específicos nos quais os padrões analisados possuem strokes perpendiculares a linha de rastreamento. Um exemplo de uma aplicação deste tipo pode ser encontrada em [75]. Outros trabalhos [74] e [81], variam continuamente a direção de rastreamento de, por exemplo, 45 ou 90 graus.
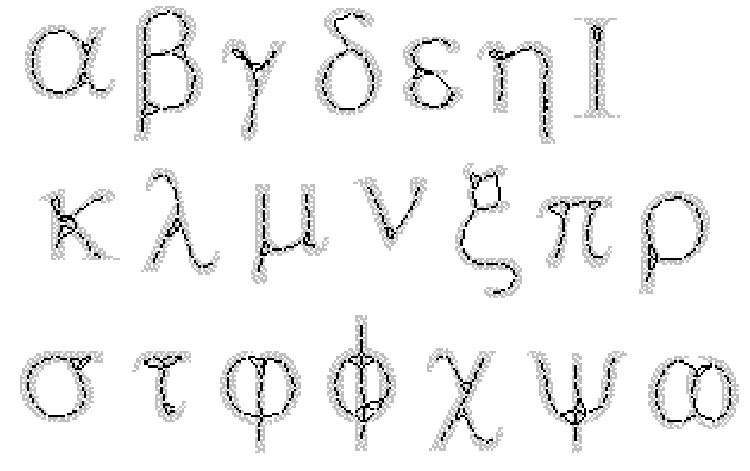
- Aplicações
- Conclusão
- Bibliografia
Como já foi dito, vantagens como, por
exemplo, a possibilidade de reduzir a quantidade de dados, bem como o fato
de que a análise de formas pode ser feita mais facilmente sobre
padrões de esqueletos (simplificação), faz com que
a esqueletonização seja empregada como técnica de
pré-processamento de imagens nas mais diversas aplicações.
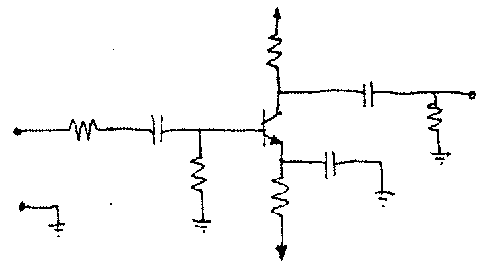
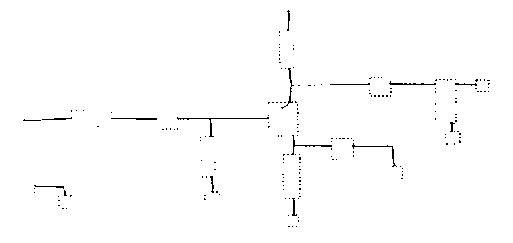
Recentemente (2000), uma aplicação bastante criativa da esqueletonização foi proposta por Edwards e Chandran. O problema consistiu em reconhecer automaticamente circuitos elétricos desenhados a mão. Na solução encontrada, a imagem digitalizada do circuito elétrico (Figura 7a) é pré-processada para remoção de ruído e binarizada. Em seguida, o algoritmos paralelo de Zhang e Suen é empregado para obter-se uma representação limpa e totalmente conectada através de linhas finas (esqueleto, Figura 7c). Em seguida, os nós do circuito (cruzamento entre dois caminhos de corrente) e os componentes são seguimentados através de limiares (thresholds), Figura 7a. Enquanto os nós são classificados através de análise sintática, os componentes são classificados através de relações vetoriais entre linhas retas e representações poligonais (modelos). Usando a esqueletonização, os nós têm um coeficiente de acerto de 86 % e os componentes de 92 %.
(a)
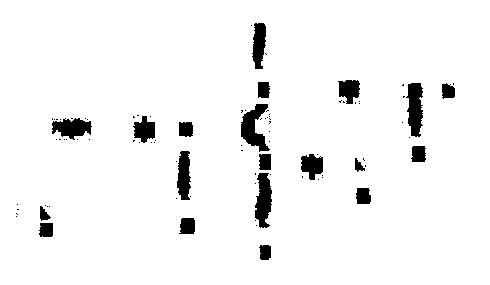
(b)
(c)
Figura 7 – (a) circuito original; (b) componentes e nós identificados, e; (c) conexões identificadas através de esqueletonização.
Em um artigo mais recente (2001), outro problema
foi solucionado com o algoritmo de Zhang e Suen: o reconhecimento, em tempo-real,
de gestos feitos com a mão para aplicações em teleconferência.
Nesta aplicação, quando a mão é detectada,
deve-se reconhecer um gesto através do número de dedos na
imagem. Para isto, a imagem da mão é segmentada usando um
algoritmo que detecta o tom de pele, e a esqueletonização
é aplicada. Então, a análise do esqueleto permite
detectar o número de dedos visíveis. Com isso, o gesto é
determinado. Os resultados (Figura 8), mostram boa performance.
 |
 |
Figura 8 – Reconhecimento de gestos em tempo-real baseado em esqueletonização.
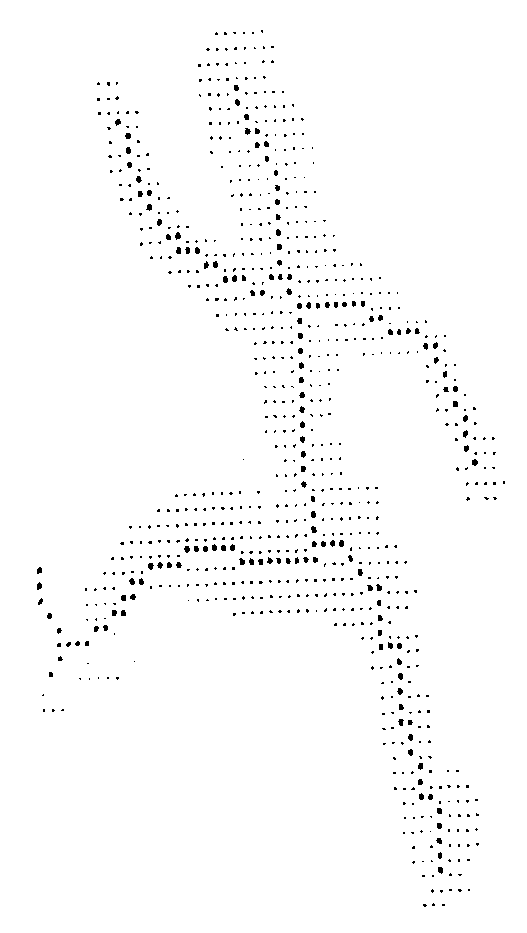
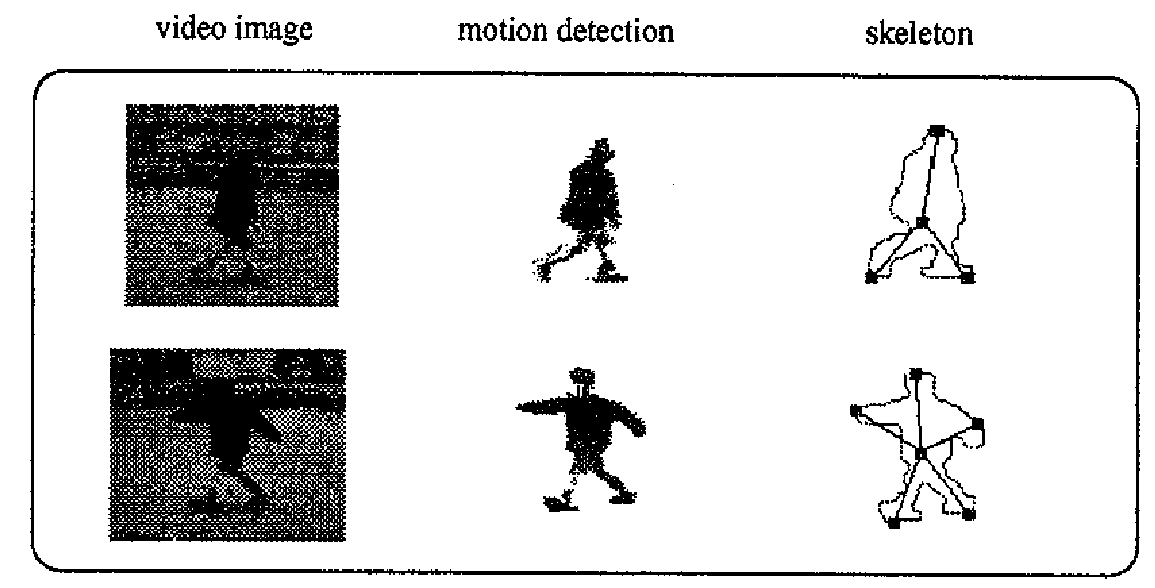
Outro trabalho que também envolve vídeo em tempo-real foi realizado por Fujiyoshi e Lipton. Agora, o objetivo é analisar o movimento de um alvo humano. Para isto, quando um alvo em movimento é detectado, a sua borda é extraída (Figura 9) e o esqueleto do padrão resultante é calculado. O interessante é que o esqueleto resultante é sempre na forma de uma estrela de cinco pontas (cabeça, braços e pernas), Figura 10. Desta estrela, são determinados a postura e o movimento cíclico. Com isso, pode-se determinar atividades como correr e andar, e a andatura (modo de andar) do alvo. Devido ao uso da esqueletonização, o sistema não requer um modelo do corpo humano ou um grande número de pixels para o alvo, o que torna-o bastante barato.
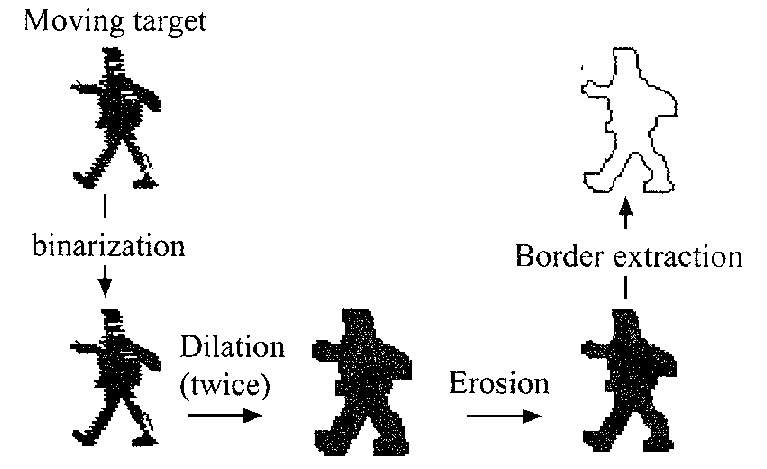
Figura 9 – Extração da borda de um alvo.
Um método de detecção e extração de esqueletos das artérias coronárias em um angiograma coronário foi proposto por Haris et al. Os angiogramas constituem a ferramenta mais utilizada na identificação de doenças coronárias. A maior incidência deste tipo de doença está relacionado à arteriosclerose que resulta na diminuição do suprimento de sangue no músculo do coração. A análise visual de um angiograma coronário pode fornecer um diagnóstico qualitativo, mas, para toma decisões médicas para o tratamento de pacientes com doenças coronárias, o uso de um sistema automático para auxílio em uma análise mais objetiva e precisa é importante. Em vista disto, os resultado conseguidos por são animadores Haris et al (Figura 11).

Figura 11 – Resultado da extração das artérias coronárias em um angiograma como o uso de esqueletonização.
Na literatura, parece ser geral a idéia
em torno dos requisitos necessários a um algoritmo de esqueletonização.
Estes requisitos incluem a conservação das propriedades topológicas
e geométricas, isotropia, reconstrubilidade, e rapidez. Portanto,
os métodos da seção anterior, que não são
baseados em pixels, são eficientes em termos de número de
operações desejadas. Contudo, são impossibilitados
de preservar maiores detalhes dos padrões, desde que eles usualmente
são baseados na localização e conexão entre
si de certos pixels chaves. Estes procedimentos são geralmente usados
em aplicações que a detecção de tais pontos
é suficiente. Um exemplo deste tipo de aplicação é
o OCR. Em geral, entretanto, a ênfase da maioria dos trabalhos reside
em algoritmos paralelos para aumentar a velocidade de processamento.
Reconstrubilidade, ou a habilidade de regenerar o padrão original a partir do esqueleto, é uma medida da eficiência com a qual o esqueleto representa o padrão original. Estes critério é geralmente satisfeito por algoritmos baseados no eixo médio (MAT) e outras transformações baseadas em distâncias [este].
Isotropia ou invariância a rotações é quase impossível de ser alcançada em algoritmos interativos. Nos algoritmos seqüenciais, o resultado depende da ordem na qual os pixels são examinados, e nos algoritmos paralelos que removem um ou dois tipos de pontos de borda em cada subinteração, o resultado depende da ordem das subinterações. Exemplos de resultados não-isotrópicos destes algoritmos podem ser vistos em [8]. Ao mesmo tempo, MAT não são invariantes sobre rotações devido a falta de algoritmos baseados em mapas de distância euclidiana verdadeiros, tal que resultados diferentes podem ser obtidos sobre certas orientações (veja [este] para maiores informações).
Manter a conectividade e a topologia em algoritmos de esqueletonização é um problema que pode ser resolvido de diversas formas. Em algoritmos seqüenciais, por exemplo, é suficiente examinar os pontos de uma vizinhança de 3 x 3 do ponto de vista do número de cruzamento. Algoritmos paralelos resolvem os problemas dividindo cada ciclo em subinterações ou considerando uma vizinhança maior em uma subinteração.
Preservação das propriedades geométricas, entretanto, parece ser a maior dificuldade do problema [este]. A dificuldade reside no fato de que, para obter-se simplicidade no algoritmo e na computação, é desejável considerar apenas vizinhanças pequenas, mas isto torna o algoritmo incapaz de prover informação estrutural do tipo que é necessária, por exemplo, para distinguir entre ruídos spúrios e genuínos pontos do esqueleto. Para prevenir erosão excessiva e a criação de pontos espúrios, várias tentativas têm sido feitas (ver [18], [70], [50] e [118]).
Para concluir, é necessário mencionar
que a comparação da qualidade dos esqueletos gerados é
subjetiva, ou seja, ainda não definiu-se medidas absolutas de propriedades
como conectividade, ruídos na forma de saltos no esqueleto e erosão.
Quando um novo autor propõe um novo algoritmo, é inevitável
compara-lo com as já existentes, mas, geralmente, isto é
feito de forma inconclusiva com uma ou duas imagens.
- Arcelli, Kwok, e Sanniti di Baja, "Medial lines by parallelwise erosion of sucessive contour pairs", IEEE Region 10 Conference, pp. 66-70, 1992.
- Farkas e Chudý, "Modified dynamic cell structures as a thinning algorithm", 1996.
- Gonzalez e Woods, "Digital Image Processing", Ed. Addison-Wesley, 1986.
- Alcorn e Hoggar, "pré-processing of data for character recognition", Marconi Rev., vol. 32, pp-61-81, 1969.
- Anônimo, "A thinning algorithm basead on prominence detection", Pattern Recogn, vol. 13, no. 3, pp 225-235, 1981.
- Arcelli, "Parttern Thinning by contour tracing", Comput. Graphics Image Processing, vol. 17, pp 130-144, 1981.
- Baruch, "Line thinning by line following", Patt. Recogn. Lett., vol. 8, no. 4, pp 271-276, 1988.
- Bel-Lan e Montoto, "A thining transform for digital images", Signal Processing, vol. 3, no. 1, pp37-47, 1981.
- Beun, "A flexible method for automatic reading of handwriten numerals", Philips Tech. Rev., vol. 33, no. 5, pp. 89-101; 130-137, 1973.
- Chen e Hsu, "A modified fast parallel algorithm for thinning digital patterns", Patter Recogn. Lett., vol. 7, no. 2, pp 99-106, 1988.
- Deutsch, "Preprocessing for character recognition", in Proc. IEEE NPL Conf. Patt. Regogn, 1968, pp179-190.
- Dinnen, "Programming pattern recognition", in Proc. Wets. Joint Comput. Conf., 1955, pp 94-100.
- Govindan e Shivaprasad, "A pattern adaptative thinning algorithm", Pattern Recog., vol. 20, no. 6, pp 623-637, 1987.
- Hall, "Fast parallel thinning algoritms: Parallel speed and connectivy preservation", Comm. ACM, vol. 32, no. 1, pp 124-131, 1989.
- Anônimo, "Linear skeletons from square cupboard", in Machine Intell., 1969, pp 403-420, vol. 4.
- Anônimo, "Comparison of thinning algoritms on a parallelprocessor", Image Vision Comput., vol. 1, no. 3, pp 115-132, 1983.
- Izzo e Coles, "Blood-cell scanner identifies rare cells", Electron, vol. 35, pp 52-53, 1962.
- Kirsch, Cahn, Ray e Urban, "Experiments in processing pictorial information with a digital computer", in Proc. East. Joint Comput. Conf., 1957, pp 221-229.
- Wang, "An improved fast parallel thinning algorithm for gigital patterns", in Proc. Int. Conf. Comput. Vision Patt. Recogn., 1985, pp 364-367.
- Moayer e Fu, "A syntatic approach to fingerprint pattern recognition", Pattern Recogn., vol. 7, pp 1-23, 1975.
- Mundy e Joyson, "Automatic visual inspection using syntatic analysis", in Proc. Int. Conf. Patt. Recogn. Image Processing, 1977, pp 144-147.
- Nguyen e Sklansky, "A fast skeleton-finder for coronary arteries", in Proc. 8th Int. Conf. Patt. Recogn., 1986, pp 481-483.
- Ogawa e Taniguchi, "Thinning and stroke segmentation for handwritten Chinise character recongnition", Patt. Recogn., vol. 15, no. 4, pp 299-308, 1982.
- Anônimo, "Algorithms for Graphics and Image Processing", 1982, pp 195-214.
- Preston, "The CELLSCAN system – A leucocyte pattern analyzer", in Proc. West. Join Comput. Conf., 1961, pp 173-183.
- Rosenfeld e Davis, "A note on thinning’, IEEE Trans. Syst. Man Cybern., vol. 25, pp 226-228, 1976.
- Sherman, "A quasitopological method for the recognition of line patterns", in Proc. Int. Conf. On Inform. Processing, 1959, pp 232-238.
- Stefanelli e Rosenfeld, "Some parallel thinning algorithms for digital pictures", J. ACM, vol. 18, no. 2, pp 255-264, 1971.
- Suzuki e Abe, "Binary picture thinning by an interative parallel two-subcycle operation", Patt. Recogn., vol. 10, no. 3, pp 297-307, 1987.
- Anônimo, "A fast and flexible thinning algoritm", IEEE Trans. Comput., vol. 38, no. 5, pp 741-745, 1989.
- Zhang e Suen, "A fast parallel algorithm for thinning digital patterns", Comm. ACM, vol. 27, no. 3, pp 236-239, 1984.
Contato:
Tel.: +55-48-331 7552/9498 |



