Visão Computacional

1.  Representação de 
     imagens
2.  Filtragem de imagens
3.  Detecção de Bordas
4.  Segmentação Simples
5.  Crescimento de Regiões
6.  Segmentação com
     Filtros
7.  Segmentação a Cores
8.  Análise de Texturas
9.  Análise de Texturas
     Multiescalar
10. Redes Neurais
11. Morfologia Matemática
12. Convolução
13. Esqueletonização
14. Técnicas Estatísticas
15. Fractais
16. Reconhecimento de
      Formas
17. Representação de 
      Objetos
18. Quadtrees e Octrees
19. Visão Estereo
20. Inteligência Artificial
21. Controle de qualidade
22. Robótica
23. Medicina
24. Sensoriamento remoto

Prof. Aldo von Wangenheim 
Currículo...
Publicações
Pesquisa
Projetos
Ensino de Graduação
Ensino de Pós Graduação 
Cursos

Você lê?

• Revisão de Conceitos
• Introdução
• Histórico
• Fourier x Wavelet
• Análise Wavelet
• Análise Wavelet Packet
• Wavelets para Análise de Textura

Aqui estão alguns dos conceitos de álgebra linear fundamentais para o estudo e entendimento de Wavelets.

• Espaço vetorial ou linear

• Para todo a, b Î Â e para todo u, v Î V, au + bv Î V.
• Existe um único elemento 0 Î V tal que:
• para todo u Î V, 0u = 0;
• para todo u Î V, 0 + u = u.

• Bases e dimensões

• Corpo

Um conjunto F ¹ 0 é um corpo comutativo se existem mapeamentos de F x F ® F: (a , b ) ®a + b e de F x F ® F: (a , b ) ®ab , denominamos adição e multiplicação, respectivamente. Ou seja, um corpo é um conjunto munido de algumas operações sobre seus elementos, as quais se comportam como a adição, subtração, multiplicação e divisão, usuais de números, no sentido de que elas obedecem certas propriedades:
• a + (b + g ) = (a + b ) + g
• a + b = b + a
• $ 0 Î F tal que a + 0 = a
• $ -a Î V para o qual a + (-a ) = 0
• ab = ba
• (a b ) g = a (b g )
• $ 1 Î F /{0} tal que a 1= a
• $ a^{-1 Î}F /{0} tal que a a^-1= 1
• a (b + g ) = a b + ag

• Produto interno e Ortogonalidade

Seja K o corpo dos números reais ou complexos e V um espaço vetorial sobre K. Um produto interno sobre V é o um mapeamento < , >: V x V® K: (u, v) <u, v>. Denominamos o par (V, < , > ) de espaço com produto interno ( ou espaço pré-Hilbert) sobre K se as seguintes propriedades são observadas.

Para todo u, v, w Î V e aÎ K, devemos ter:

• <u + v, w> = <u , w> + <v , w>
• <a u , w> = a <u , w>

• ---

  <u , v> = <v , u>
• <u , u> ³ 0
• <u , u> = 0 Þ u = 0
< , > é denominado de produto interno.

Um dos usos mais importantes do produto interno é para formalizar a idéia de ortogonalidade. Dois vetores u e v são ditos ortogonais se <u ,v> = 0.

Uma base ortogonal é uma base que consiste de vetores ortogonais entre si.
 
 

• Normas e normalização

Wavelets são funções que satisfazem a certos requisitos matemáticos e são usadas na representação de dados ou de outras funções. Elas utilizam a idéia de aproximação usando a superposição de funções. Esta idéia tem sua origem no trabalho de Joseph Fourier, que no século XIX descobriu que poderia utilizar senos e cosenos para representar outras funções.

A novidade em relação a Fourier é que a análise em wavelets não é feita segundo a freqüência mas sim segundo a escala. Os algoritmos wavelet processam dados em diferentes escalas e resoluções, permitindo que sejam vistos tanto o global quanto os detalhes.

Além da análise de imagens, foco deste trabalho, as wavelets possuem um vasto campo de aplicações. A compressão de imagens pode ser considerada a mais conhecida das aplicações, mas existem ainda aplicações no processamento de sinais, astronomia, acústica, engenharia nuclear, neurofisiologia, música, ótica, fractais e em aplicações matemáticas puras, como na resolução de equações diferenciais parciais.

Existem algumas famílias de wavelets, são elas:

• Haar: É a primeira e a mais simples de todas. É descontínua e equivale a Daubechies 1 (db1).
• Daubechies: Compactly-supported orthonormal wavelets.
• Biortogonal: Apresenta a propriedade de fase linear, que é necessária na reconstrução de sinais e imagens. Utiliza duas wavelets, uma para decomposição e outra para reconstrução, o que gera propriedades interessantes.
• Coiflets: A função wavelet possui 2N momentos iguais a zero e a função escala tem 2N-1 momentos iguais a zero.
• Symlets: São wavelets simétricas. Foi proposta como uma modificação da família Daubechies pela própria, possuindo caracterísitcas similares as desta família.
• Morlet: Não possui função escala e é explícita.
• Mexican Hat: Também não possui função escala mas não é explícita.
• Meyer: A wavelet e a função escala estão definidas no domínio de freqüência.

Na história da matemática, a análise wavelet mostra diferentes origens. Muitos dos trabalhos foram realizados por volta de 1930.

Antes de 1930, Joseph Fourier (1807) iniciou o estudo de wavelet com suas teorias de análise de freqüência, afirmando que qualquer função f(x) de período 2p é a soma:

onde

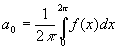
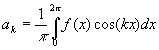
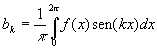
Depois de 1807, os matemáticos analisando o sentido das funções, da convergência da série de Fourier e sistemas ortogonais, migraram da noção de análise de freqüência para a noção de análise de escala. Isto é, analisando f(x) criando estruturas matemáticas que variam em escala. A análise de escala é menos sensível a ruídos porque ela mede a flutuação média do sinal em diferentes escalas.

A primeira vez que o termo wavelet foi mencionado foi em um apêndice da tese de Alfred Haar (1909). As wavelets Haar não são continuamente diferenciáveis, o que de certo modo limita suas aplicações.
 
 

Após 1980, Y. Meyer construiu a primeira wavelet não trivial. Diferente das wavelets de Haar, elas são continuamente diferenciáveis.

Alguns anos depois, Ingrid Daubechies construiu um conjunto de funções base wavelet ortonormais, que são, talvez, as mais elegantes e se tornaram um marco nas aplicações de wavelets.
 
 
 

A análise de Fourier e as wavelets têm uma ligação muito forte.

Similaridades

A transformada rápida de Fourier (fft) e a transformada discreta de wavelet (dwt) são ambas operações lineares que geram uma estrutura de dados que contém segmentos de vários tamanhos, usualmente os preenche e os transforma em um vetor de dados diferente de tamanho 2ⁿ.

As propriedades matemáticas das matrizes envolvidas nas transformadas são também similares. A inversa da matriz da transformada tanto para o fft, quanto para a dwt é a transposta da original. Como resultado ambas as transformadas podem ser vistas como uma rotação no espaço da função para um diferente domínio. Para a fft, este novo domínio contém funções base que são senos e cosenos. Para a transformada wavelet, este novo domínio contém funções base mais complicadas chamadas wavelets, chamadas mother wavelets. Além dessas, as transformadas fft e dwt possuem outras similaridades.

Diferenças

A mais importante diferença entre estes dois tipos de transformadas é que funções individuais wavelets estão localizadas no espaço. As funções seno e coseno, usadas na fft, não estão. O fato das funções seno e coseno não estarem localizadas no espaço pode ser entendido com o seguinte exemplo:

• Se tocarmos em piano a nota do e depois a nota mi, e analisarmos a gravação destes sons utilizando Fourier, saberemos que duas notas foram tocadas, mas não teremos como dizer qual foi a seqüência. Ou seja, a análise deste som (do mi) será exatamente igual a de mi do, com um pico na freqüência do do e com um na freqüência do mi.

Uma maneira de se enxergar as diferenças de resolução tempo-freqüência entre a transformada de Fourier e a transformada wavelet é olhar para a cobertura da função base no plano tempo-freqüência.

Uma vantagem da transformada wavelet é que o tamanho da janela varia.

A transformada wavelet não possui um único conjunto de funções base, como acontece com a transformada de Fourier, que utiliza apenas as funções senos e cosenos. A transformada wavelet possui um conjunto infinito de funções base, assim, a análise wavelet fornece acesso imediato à informação que pode estar escondida em outros métodos tempo-freqüência, como a análise de Fourier.
 

Em análises wavelet, um sinal é dividido em aproximação e detalhe. Esta aproximação é então dividida em uma aproximação de segundo-nível e detalhe, e o processo se repete. Para uma decomposição de nível-n, há n + 1 caminhos possíveis para decompor ou codificar o sinal.
 

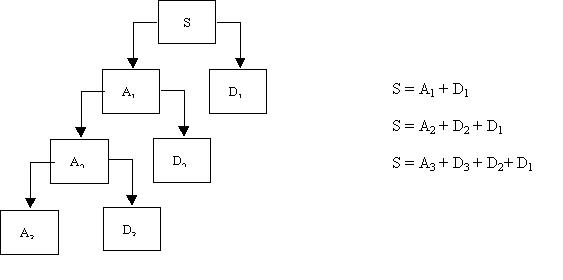
Fig. 1 – Árvore da análise wavelet.
 
 
 
 

Wavelets em uma dimensão

Sendo V^j um espaço vetorial, definimos uma função base , chamada função escala. A base mais simples para V^j é dada pelo conjunto de funções janela escaladas e transladadas:

: = , onde

Por exemplo:

Fig. 2 – Quatro funções janela formando uma base para V².
 

O próximo passo é escolher um produto interno definido no espaço vetorial V^j. O produto interno padrão é dado por:

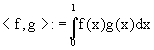
sendo f e g funções pertencentes ao espaço V^j.

Definimos agora um novo espaço vetorial W^j como o complemento ortogonal de V^j em V^j+1. Podemos pensar em W^j como o espaço que contém os detalhes em V^j+1, que não podem ser representados em V^j, espaço das aproximações.

Wavelet é uma coleção de funções  linearmente independentes que geram o espaço W^j. Estas funções base possuem as seguintes características:

1. As wavelets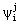, base de W^j, juntamente com as funções base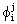 de V^j formam uma base para V^j+1.
2. Todas as wavelets 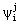 de W^j são ortogonais a todas as funções base 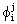 de V^j em um certo produto interno escolhido.
3. Todas as funções wavelets

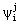
As wavelets de Haar são definidas por:

Onde,

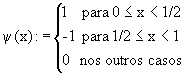
A mesma imagem I(x) pode ser reescrita em termos de funções base em V¹ e W¹. Armazenando agora, no lugar dos 4 pixels originais, duas médias e dois coeficientes de detalhe.

Finalmente, a imagem pode ser reescrita como uma soma das funções base em V⁰, W⁰ e W¹. Agora teremos I(x) representada por uma aproximação (), um detalhe grosseiro () e dois detalhes refinados ().

Estes coeficientes são a transformada wavelet de Haar da imagem original.
 
 
 

O método wavelet packet é uma generalização da decomposição wavelet que oferece um limite de possibilidades mais rico para a análise de sinais.

Em análises wavelet packet, os detalhes bem como as aproximações podem ser divididas, gerando 2ⁿ caminhos diferentes para a codificação do sinal. A árvore de decomposição da wavelet packet fica da seguinte forma:
 

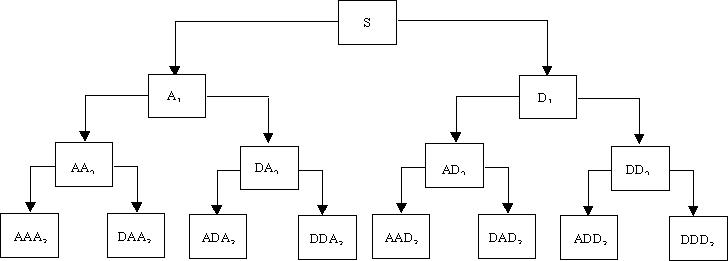
Fig. 3 – Árvore da análise wavelet packet.
 

As análise wavelet packet permitem que um sinal S seja representado como A₁+AAD₃+DAD₃+DD₂. Isto é um exemplo de uma representação que não é possível utilizando a análise wavelet ordinária.
 

• Que família de wavelet utilizar?

• Resultados em análise de imagens

1. Analisando a imagem Calçada2

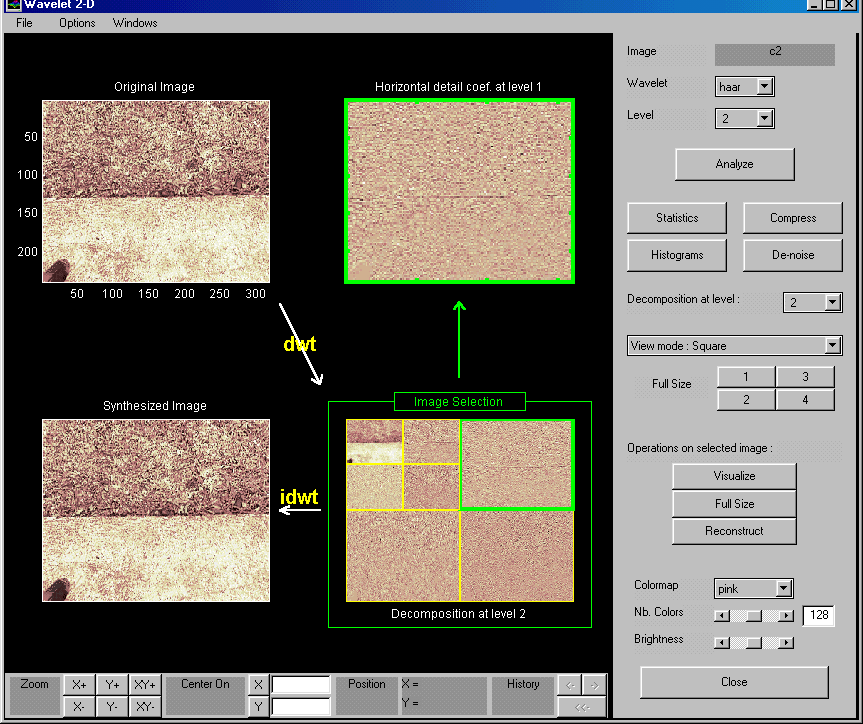
Analisando pequenos pedaços das imagens de cada textura (grama / calçada).

Da imagem, pegamos três pedaços da grama e três da calçada, para análise dos coeficientes gerados em cada uma.

Exemplo: C21 – Um pedaço da imagem da grama

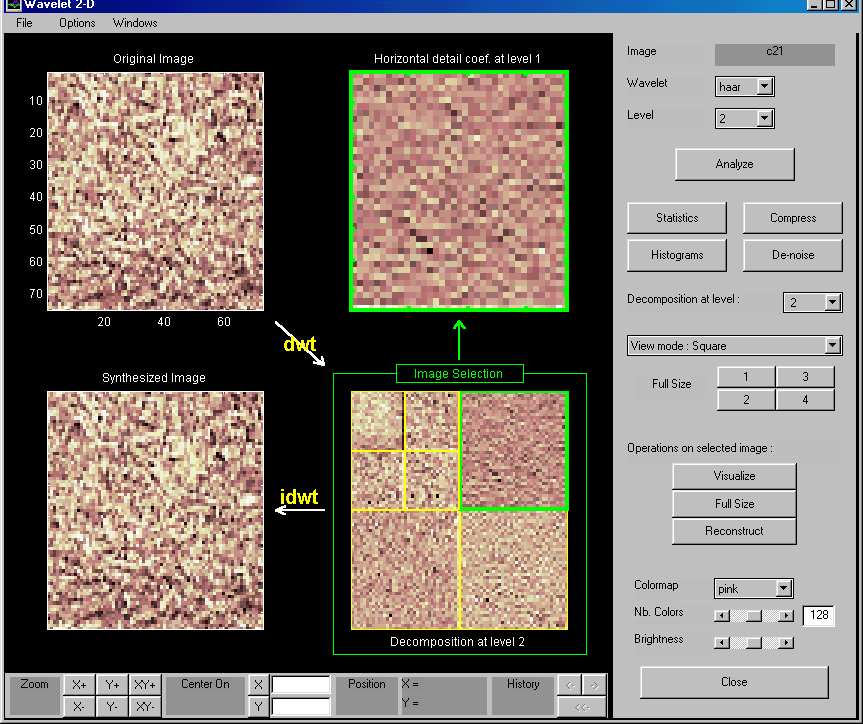
Analisando os coeficientes

1. imagem Calçada2

 

 
 
 
 
 
 
 

Para a análise da imagem da calçada geramos seis sub-imagens, três contendo apenas textura de grama e três contendo apenas textura de calçada.

Foram gerados os coeficientes para cada uma destas imagens, utilizando Biortogonal 3.7, a fim de locarlizarmos os coeficientes que classificassem as diferentes texturas.
 
 

Coeficientes para as três imagens de grama:



Coeficientes para as três imagens de calçada:


 

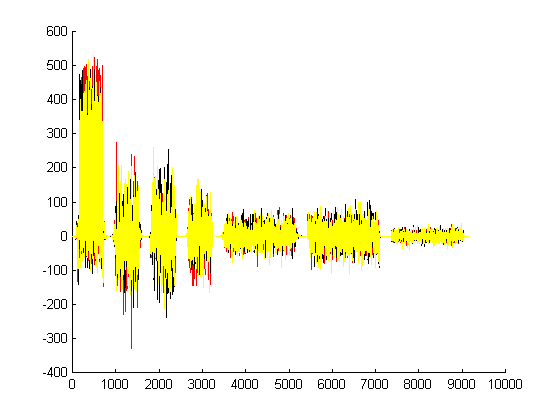
Sobrepondo todos os coeficientes:


 
 
 

2. imagem Árvores2

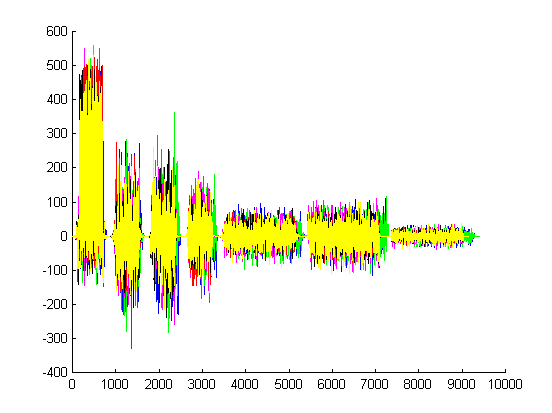
Foram gerados os coeficientes para cada uma destas imagens, utilizando Daubechies-4, a fim de locarlizarmos os coeficientes que classificassem as diferentes texturas.
 
 
 

Coeficientes para as imagens do primeiro tipo de árvore:

 

Coeficientes para as imagens do segundo tipo de árvore:

 
 

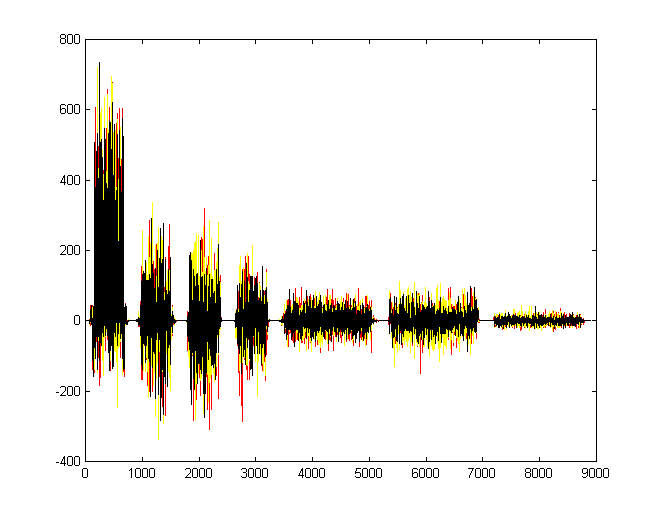
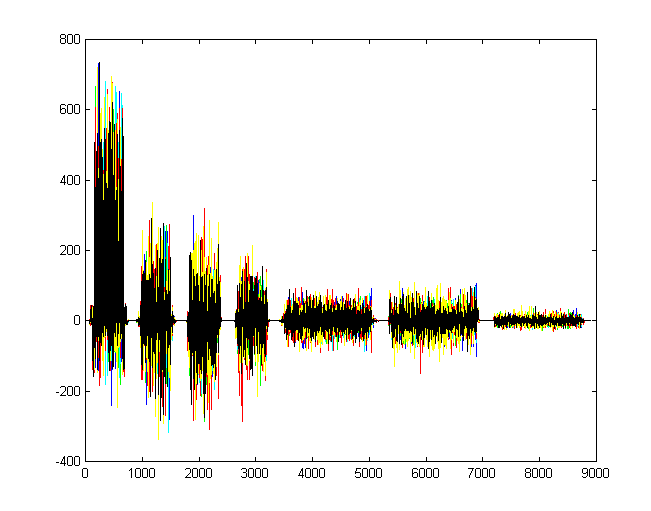
Sobrepondo todos os coeficientes:

 
 

Referências Bibliográficas:

Gomes, J., Velho, L. From Fourier Analysis to Wavelets. 1998.

Graps, A. An Introduction to Wavelets. 1995.

Misiti M. et alli. Wavelet Toolbox: for use with Matlab. 1997.

Scheunders, P. et alli. Wavelet-based Texture Analysis. 1997.

Scheunders, P. et alli. Wavelets for Texture Analysis. 1997.

Stollnitz, E. J., DeRose T., Salesin D.H. Wavelets for Computer Graohics: a primer. 1995.

Strang, Gilbert. Creating and Comparing Wavelets. 1994.
 

Contato: Tel.: +55-48-331 7552/9498 FAX: +55-48-331-9770 awangenh@inf.ufsc.br