
Visão Computacional
1. Representação de
imagens
2. Filtragem de imagens
3. Detecção de Bordas
4. Segmentação Simples
5. Crescimento de Regiões
6. Segmentação com
Filtros
7. Segmentação a Cores
8. Análise de Texturas
9. Análise de Texturas
Multiescalar
10. Redes Neurais
11. Morfologia Matemática
12. Convolução
13. Esqueletonização
14. Técnicas Estatísticas
15. Fractais
16. Reconhecimento de
Formas
17. Representação de
Objetos
18. Quadtrees e Octrees
19. Visão Estereo
20. Inteligência Artificial
21. Controle de qualidade
22. Robótica
23. Medicina
24. Sensoriamento remoto
Prof. Aldo von Wangenheim
Currículo...
Publicações
Pesquisa
Projetos
Ensino de Graduação
Ensino de Pós Graduação
Cursos
Técnicas de Segmentação de Imagens a Cores
Christian Cechinel
Índice
1. Introdução
2. Espaços de cor
3 Propriedades das características cromáticas
4 Segmentação baseada em pixel
4.1. Limiarização por Histogramas (thresholding)5. Segmentação por Crescimento de Regiões - Color Structure Code
4.2. Agrupamento em espaço de cor
4.3. Agrupamentos fuzzy no espaço de cor
A segmentação de imagens, ou seja, identificação de regiões homogêneas na imagem, tem sido objeto de consideráveis atividades de pesquisa nas últimas três décadas. Muitos algoritmos têm sido elaborados para imagens em escalas de cinza. Entretanto, o problema da segmentação em imagens coloridas, que carregam muito mais informação sobre objetos em cenas, tem recebido muito menos atenção da comunidade científica. Enquanto inúmeros levantamentos de técnicas para segmentação de imagens monocromáticas foram publicados, levantamentos similares para imagens coloridas não são encontrados.
Este relatório contém: um extenso levantamento de algoritmos para segmentação de imagens coloridas, uma classificação desses algoritmos de acordo com uma lista de atributos bem definida, sugestões para melhoramentos e descrições de algumas novas abordagens.
Na classificação de algoritmos para segmentação de imagens coloridas as seguintes definições serão úteis:
Segmentação de imagens coloridas é um processo pelo qual se extraem, do domínio da imagem, uma ou mais regiões conectadas que satisfaçam o critério de uniformidade (homogeneidade), o qual é baseado em características derivadas de componentes do espectro. Esses componentes são definidos em um modelo de espaço de cores escolhido. O processo de segmentação pode ser melhorado através de alguns conhecimentos adicionais sobre os objetos em cena tais como as suas propriedades ópticas e geométricas.
Talvez a característica mais importante do método de segmentação apresentado é a definição de região. Podemos identificar esta definição em quatro grandes tipos:
- Região é um componente conectado de um grupo de pixels, especificado por uma função de pertinência de classes definida num espaço de cores; Por exemplo:
- Cor do pixel está num determinado quadrante definido por um plano.;
- Cor do pixel está no poliedro dado;
- Cor do pixel está na célula de Voronoi com a representatividade dada;
- Função de pertinência fuzzy para uma classe "defuzificada" por uma operação corte-a .
- Região é um grupo (maximal) de pixels conectados para cada condição de uniformidade que é satisfeita. Por exemplo:
- Região uniforme derivada do crescimento de um bloco inicial através da união de outros pixels ou blocos de pixels.
- Região uniforme obtida através da quebra de uma região maior, que não é uniforme.
- Região é um grupo de pixels conectados unidos por uma borda de pixels criando um contorno colorido. Por exemplo, detecção de bordas através de um vetor de média ou um operador Hueckel com modelo orientado preenchendo os espaços no contorno. Observe também que, num certo sentido, regiões aqui são também uniformes, porque elas estão no grupo complementar do grupo não uniforme que a borda de pixels cria.
- Região corresponde a uma superfície ou a um objeto de material homogêneo, ou seja, regiões representam o material conectado em cena. Por exemplo, degradé, sombra e reflexo não possuem influência no resultado de uma segmentação de imagem, entretanto eles mudam os valores de cor na imagem.
Além disso, técnicas de segmentação empregando a definição de região do tipo 4 pertencem a uma nova classe de métodos de visão computacional, que têm sido categorizados durante os últimos anos como physics based vision methods. O leitor desta revisão pode facilmente chegar a essas técnicas através dessa definição suplementar de região.
Resumindo, chamamos o tipo 1 de definição de regiões baseada em pixel, o tipo 2 de definição de regiões baseada em área, o tipo 3 de definição baseada em borda, e o tipo 4 de definição fisicamente baseada.
Enquanto as categorias 2 e 3 são muito bem conhecidas através da literatura (veja por exemplo, a revisão de Pal e Pal [54]), a categoria 1 envolve técnicas como histogramação e "clusterização". A categoria 4 usa modelos de reflexão baseados nas propriedades do material em cena. Esta última categoria não tem recebido a devida atenção nas revisões já existentes sobre segmentação de imagem.
Outro aspecto importante dos métodos de segmentação é o espaço de cor do qual as características da cor são computadas (por exemplo, o espaço RGB com distância Euclidiana de cor).
Cada técnica de segmentação é normalmente baseada em alguns modelos matemáticos (teoria) e/ou abordagens algorítmicas (como agrupamentos fuzzy, campos aleatórios Markov, procedimento recursivo, algoritmo bottom-up). Além disso, são especificadas através de categorias comuns de métodos matemáticos básicos.
A maioria das técnicas de segmentação leva em consideração algo sobre a cena que é visto na imagem ( como: objetos são poliedros feitos de materiais dielétricos). Este é um conhecimento adicional atribuído ao método de segmentação determinado.
Freqüentemente, o método de segmentação especificado foi projetado para alguma aplicação real. E este é o último aspecto que gostaríamos de discutir em relação à caracterização de uma técnica em particular.
Em resumo, os seguintes atributos serão avaliados pelas técnicas de segmentação revisadas: definição de região, método matemático básico, espaço de cor, conhecimentos adicionais, aplicações. Também pretende-se identificar características cromáticas que poderiam ser úteis em casos como os de bordas de cor (veja Jordan e Bovik [39]).
Para clara comparação de contribuições das
pesquisas e para maiores referências, decidiu-se apresentar os trabalhos
na ordem em que os atributos listados acima (estendendo-se para o ano,
autor) são avaliados e, então, complementá-los com
uma descrição mais detalhada. O título do trabalho
é colocado no cabeçalho da subseção. Nossas
soluções são marcadas por * * ** no campo do ano.
2. Espaços de cor
Muitos espaços de cor são utilizados hoje em dia. Para figuras obtidas por câmeras digitais o mais popular é o modelo RGB. De acordo com a teoria de tristimulus (Wyszecki and Stiles [79]), a cor pode ser representada por três componentes, resultantes de três diferentes filtros de cores Sx, X= R,G,B, sobre brilho da luz e E(l )de acordo com as equações:
![]() ,
, ![]() ,
,![]() (2)
(2)
Observe que, r + g + b = 1, logo alguns autores (como Nevatia [50,51]) utilizam apenas os componentes rg, adicionando um independente, como por exemplo um tipo de luminância
![]()
Existe vários modelos de cor baseados na percepção humana da cor. Tais modelos se referem à componentes de tom (hue), saturação (saturation) e intensidade (intensity). A maioria deles segue o sistema de cor Munsell (Wyszecki [79]). Por exemplo, o modelo HSI é transformado a partir do modelo RGB usando as seguintes fórmulas:
![]() (5)
(5)
Enquanto I e S são de alguma maneira arbitrariamente modelados, a fórmula para H é facilmente derivada se fizermos uma projeção do eixo RGB no plano R + B+ G = 0 como mostra a seguinte figura:
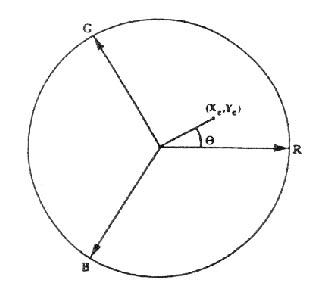
Se diferenças absolutas de tom (H) devem ser calculadas, então a aritmética modular especial deverá ser utilizada:
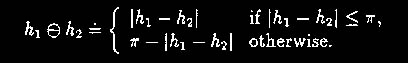 (6)
(6)
Como em pequenas intensidades e pequenas saturações, o tom (H) é determinado com muito pouca precisão (veja a prova abaixo), então qualquer comparação de cor deve evitar diminuições de tom nessa situação (pequenas intensidades e pequenas saturações). Uma solução prática é utilizar a diferença absoluta da intensidade.
Outro espaço de cor menos conhecido e também humanamente orientado é o modelo TekHVCT, que utiliza (V, C, H) coordenadas modelando intensidade, saturação e tom, respectivamente:
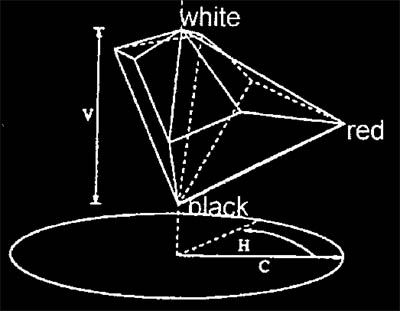
Se mapearmos (intensidade, saturação, tom), isto é, (i, s, h) coordenadas sobre o volume sólido de cor de Munsell, então a distância Euclidiana entre as cores (i1, s1, h1) e (i2, s2, h2) poderia ser calculada por intensidades que são maiores que 10% do seu intervalo (25 em [0,255]):
![]() (7)
(7)
Coordenadas tristimulus RGB excluem algumas cores visíveis. Elas também dependem de sensores físicos. Por essa razão, uma equipe internacional, o comitê CIE fixou as coordenadas tristimulos XYZ. Elas podem ser produzidas a partir das coordenadas tristimulos RGB através de uma transformação linear. Entretanto, a matriz de transformação precisa ser determinada empiricamente. Por exemplo, a matriz para o sistema primário de recepção NTSC, é:
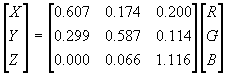
Se as coordenadas XYZ são conhecidas, diferentes espaços CIE podem ser construídos. Foi verificado que o espaço CIE (Lab) é perceptualmente uniforme e traz bons resultados para segmentação de figuras coloridas.
![]() (8)
(8)
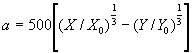 (9)
(9)
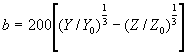 (10)
(10)
onde (Xo, Yo, Zo) são valores XYZ para a referência branco.
Outro espaço de cor CIE usado nessa área é o espaço CIE (Luv):
![]() (11)
(11)
![]() (12)
(12)
Alguns autores usam sistemas de cor para TV, YIQ do sistema americano
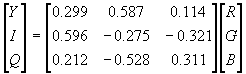 (13)
(13)
e, YUV do sistema europeu:
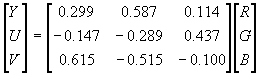 (14)
(14)
A partir das coordenadas CIE, existe uma maneira simples de se obter as coordenadas de tom e saturação:
![]() (15)
(15)
![]() (16)
(16)
Para modelos CIE, como o de medida de distância entre duas cores, a distância Euclidiana é usada. Entretanto, isso é experimentalmente justificado apenas para os espaços CIE (Luv) e CIE (Lab).
3 Propriedades das características cromáticas
Perez e Koch têm demonstrado ([56]) as vantagens e algumas desvantagens do tom e dos componentes RGB normalizados. Suas conclusões são baseadas em modelos simplificados da propagação da luz utilizados em gráficos computacionais. Entretanto, alguns experimentos validam essas suposições com bom grau de precisão.
3.1 Escala uniforme e invariância conversível
Através de manipulações algébricas simples é fácil provar os 4 fatos a seguir:
- O Tom é invariante na escala uniforme dos componentes RGB:
- Os componentes RGB normalizados são invariáveis na escala uniforme dos componentes RGB:
- O Tom é invariante em conversão uniforme dos componentes RGB:
- Componentes RGB normalizados não são invariáveis em conversão uniforme dos componentes RGB:
![]()
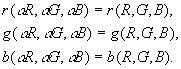
![]()
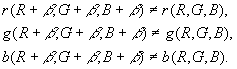
3.2 Particularidade do Tom (H) quando próximo do RGB zero
Quando R=G=B=0, podemos ver pela fórmula 5 que o tom é indefinido.
Além disso, um desvio do ponto de cor de (0, 0, 0) para ( (1- a ) Î , aÎ , 0) dá, ao coeficiente de peso fixado ae a qualquer Î, o valor de tom igual a:
![]()
Isto implica que mesmo para um pequenoÎ o tom pode variar de zero ( para a =0) a 2p /3 (para a =1).
Em representações discretas de computador (R, G, B), a mínima mudança ocorre em passos de unidade de cada componente. Consequentemente provas mais convincentes da particularidade do tom próximo a zero é tomada H(1,0,0) = 0 e H(0,1,0) = 2p /3.
A mudança da cor de (x,x,0) para (x +1, x, 0) altera o tom H pelo ângulo d satisfazendo a seguinte relação:
Concluindo: o cálculo do Tom para sistema de cor RGB com baixa intensidade leva a erros numéricos significantes e por isso não é recomendado.
3.3 Diminuindo transparências
Na distância d a luz do comprimento de onda l é atenuada por t (l )d. Se o meio transparente é uniforme, então t é constante e os componentes vermelhos possuem a seguinte forma:
![]()
![]()
Portanto ao passar o meio uniformemente transparente, os componentes RGB sobem uniformemente. Dessa forma, ambos, Tom e RGB normalizado são invariáveis à passagem de luz através de meios uniformemente variáveis.
3.4 Diminuindo reflexos
Alguns materiais podem interagir (local ou globalmente) com a luz de maneira a refleti-la (por exemplo vidro). Então, em alguns ângulos onde a luz cai, reflexos podem ocorrer. Manchas de reflexos na imagem criam sérios problemas para os algoritmos de segmentação. Aplicando o modelo de Phong para formação de imagem, Perez e Koch tem mostrado que usando o tom pode-se reduzir esse efeito indesejável.
A geometria de formação de imagem no modelo de Phong ([57]) é mostrada na figura a seguir:
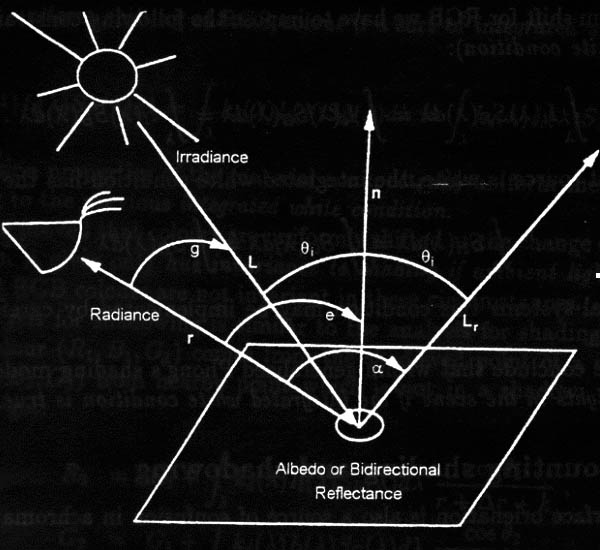
Nas equações de degrade de Phong para os tristimulus de brilho captados pelo observador provenientes de uma pequena mancha numa dada superfície consistem do ambiente, da difusão e da parte que reflete.
![]() (17)
(17)
![]()
Isso significa que componentes que não refletem são uniformemente conversíveis. Isto implica, que o tom é invariante para reflexos de fontes de luz branca, enquanto o RGB normalizado não é invariante.
Se generalizarmos a equação de Phong para um comprimento de onda arbitrário, teremos:
![]()
De acordo com a equação tristimulus 1, decompomos o componente refletor vermelho da seguinte forma:
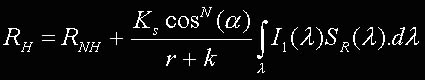
Para termos uma mudança uniforme para RGB temos que impor a seguinte restrição (chamada de condição branca integrada):
![]() (20)
(20)
Se a fonte de luz é branca, a condição branca de integrada tem a seguinte forma:
![]() (21)
(21)
Em sistemas artificiais esta condição pode ser implementada através de filtros espectrais cuidadosamente projetados.
Finalmente, concluímos que dentro do modelo generalizado de degrade de Phong, o tom ignora reflexos em cena se a condição branca integrada é verdadeira.
3.5 Diminuindo degrade e sombreamento
Mudança na orientação da superfície é também uma fonte de confusão em sistemas de visão acromática.
Assumindo o modelo de degrade de Phong e o material de um objeto não-especular (superfícies opacas) podemos eliminar a dependência do RGB em relação à orientação da superfície em algumas circunstâncias bem definidas.
Supondo que dois pontos superficiais próximos são iluminados nos ângulos q1 e q2, respectivamente. Se ignorarmos a luz ambiente, então através da equação tristimulus podemos obter as relações para os valores RGB (R1, G1, B1) (R2, G2, B2) visualizados nesses dois pontos:
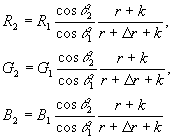
Assim as cores para dois pontos são relacionadas por operações escalares. Concluímos que para superfícies opacas, enquanto ignorada a luz ambiente, tanto o RGB normalizado quanto o tom são invariáveis a mudanças da orientação da superfície em relação à fonte de luminosa.
Se não é possível ignorar a luz ambiente, então as relações de cor têm a seguinte forma:
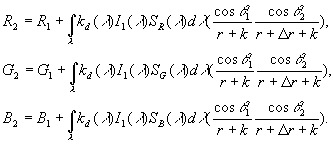
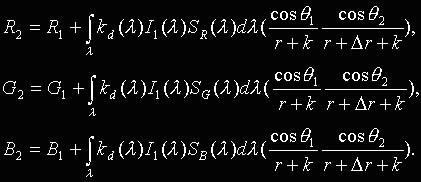
Se as propriedades de difusão do material são uniformes no espectro, então esta condição é reduzida à condição prévia de integração do branco.
Uma vez provado que as cores são uniformemente convertidas na mudança da orientação da superfície, temos invariância de tom para degrade somente se a luz ambiente é significante. Cores RGB normalizadas não são invariantes nessas circunstâncias.
Uma análise para sombreamento é similar a análise para degrade. Se assumirmos que a cor (R1, G1, B1) vem de um ponto sombreado de uma superfície e que a cor (R2, G2, B2) vem de um ponto próximo, que não está numa sombra, então, para superfícies opacas, temos:
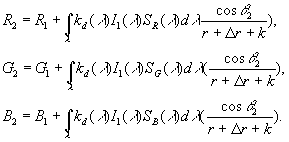
Temos uma conversão uniforme de cor quando a mesma condição 22 é satisfeita. Portanto o tom é invariante para sombras se o material é opaco, a condição branca integrada generalizada é válida, e o modelo de formação de imagem de Phong pode ser aceito. Assim como para degrade, se o material é espectralmente uniforme na difusão da luz, então a condição branca integrada é suficiente.
Experimentos ([56]) mostram que para cenas típicas, a mudança
do tom na borda da sombra é pequena, representando cerca de 3 a
5 %.
4 Segmentação baseada em pixel
Nessa seção iremos discutir técnicas de segmentação que operam no espaço de cor. Os trabalhos disponíveis podem ser amplamente divididos em três grupos:
- Técnicas baseadas em histrograma: um ou mais picos são identificados, e os intervalos que os rodeiam são utilizados em seguida no processo de classificação de pixel.
- Segmentação através do agrupamento de dados no espaço de cor: os valores de pixel são coletados em grupos com um ou mais representantes que são utilizados em seguida no processo de classificação de pixel.
- Segmentação através de fuzzy: funções de pertinência fuzzy são avaliadas para todos os pixels e para todos os blocos fuzzy definidos; blocos fixos de pixels são obtidos através do processo de "defuzzyfication" e em seguida subdivididos em regiões máximas conectadas.
4.1. Limiarização por Histogramas (thresholding)
4.1.1 Segmentação estável usando informação de cor
Autor (s): L.Bonsiepen and W. Coy ([10]).
Ano: 1991.
Definição de Região: Pixels com uma característica escalar de cor abaixo do limiar pertencem ao plano de fundo, outros pertencem ao objeto.
Métodos Matemáticos Básicos: Histograma e computação do limiar único em histogramas bimodais.
Espaços de cor: RGB normalizado a partir de onde uma característica escalar F é extraída:
![]()
Conhecimentos adicionais: Somente liquens (criando uma região conectada na imagem) e o plano de fundo estão na imagem.
Aplicações: Cor e velocidade do crescimento da população de liquens (medida pela área da região ocupada por eles) são usadas em pesquisas ambientais.
Descrição: A característica F foi encontrada na base de trezentas figuras considerando um conjunto de cerca de 1000 características de cor. Os autores não descrevem qual método foi usado para extrair F, mas uma rede neural com um único perceptron poderia resolver este problema. O limiar foi encontrado no ponto mínimo de histogramas bimodais, muito bem separados, construídos para F.
4.1.2 Segmentação de figuras utilizando o método recursivo de ruptura de região.
Autor : R. Ohlander, K. Price, e D.R. Reddy ([52])
Ano: 1978
Definição de Região: O pico do histograma em uma das nove características de cores determina o intervalo. Os pixels que caem dentro desse intervalo criam uma região e os pixels que caem fora desse intervalo criam outra. Ambos são recursivamente divididos. A região conectada que não possui um pico evidente é enviada como saída.
Métodos matemáticos básicos: Histogramação de muitas características de cor. Seleção do melhor pico. Decomposição da região em componentes conectados.
Espaço de cor: Nove características coletadas dos sistemas de cor RGB, HSI e YIQ.
Conhecimento adicional: nenhum.
Aplicação: Propósito geral.
Descrição: A seleção do pico é dirigida por uma lista de sete condições arbitrariamente fixadas. Primeiramente, todos os picos do grupo de histogramas são localizados. A lista de picos de menor prioridade é construída. O melhor pico dessa lista é determinado e valores limiares são escolhidos em cada lado desse pico.
O esquema de segmentação geral consiste nos seguintes passos:
- Coloque o domínio da imagem na lista região vazia inicial;
- Pegue a próxima região para o segmento. Se não há mais regiões PARE;
- Selecione o melhor pico. Se não houver nenhum, então envie como saída esta região uniforme e vá para o passo 1;
- Aplique o threshold;
- Selecione regiões conectadas e as adicione à lista de regiões;
- Vá para o passo 1.
4.1.3 Informação de cor para segmentação de região
Autor: Y.I. Ohta, T. Kanade, e T, Sakai ([53])
Ano: 1980
Definição de Região: Da mesma maneira que no trabalho de Ohlander, mas com somente três características I1, I2, I3.
Métodos Matemáticos Básicos: Transformação KL, ou seja, análise de componente principal com a finalidade de extrair as características de cor mais importantes. Como no trabalho de Ohlander.
Espaço de cor: Transformação do RGB para I1I2I3:
I1= (R+G+B)/3, I2 = R - B, I3 = (2G – R – B)/2
Conhecimento adicional: Nenhum
Aplicação: Propósito geral.
Descrição: O modelo I1, I 2, I3 foi obtido através da evidência experimental de que ele é uma boa aproximação para a transformação KL.
O algoritmo é muito semelhante ao de Ohlander, mas a sua apresentação é mais clara e sugere estruturas de dados para implementação mais eficiente, tanto em aspectos de tempo quanto de espaço.
- Uma máscara correspondente a toda imagem é colocada no fim da pilha.
- Se a pilha está vazia então PARE. Caso contrário, uma máscara é tomada do topo da pilha. Deixe S indicar a região representada por essa máscara.
- Os histogramas das características de cores na região S são computados.
- Se algum dos histogramas mostra picos visíveis, um par de valores do corte que separam o pico no histograma é determinado nas posições dos vales, e a imagem da característica da cor correspondente ao histograma é limitada usando os valores do corte; então a região S é partida. Caso contrário envie como saída S e vá para o passo 1.
- As regiões conectadas são retiradas. Para cada região conectada, uma máscara de região é gerada e colocada na pilha; Vá para o passo 1.
Autor: K. Holla ([32]).
Ano: 1982
Definição de Região: As montanhas nos histogramas bidimensionais dos pares de cores opostas determinam as áreas. A queda dos pixels em uma dessas áreas cria uma região. A queda dos pixels em uma oura área cria uma oura região.
Método matemático básico: Achar picos e bases no histograma bidimensional dos pares de cores opostas.
Espaço de cor: Espaço de cor contrária separando o sinal em luminance e chrominance. O plano da chrominance é dado pelos pares de cores opostas vermelho-verde e amarelo-azul.
Conhecimento Adicional: Nenhum
Aplicação: Propósito Geral
Descrição: Os valores RGB são transformados para os pares de cores opostas vermelho-verde (RG), amarelo-azul (YB), e na função de intensidade (I). Os três canais são uniformizados aplicando filtros band-pass onde as freqüências centrais dos filtros dispõem de uma proporção I: RG: YB = 4: 2: 1. Então picos e bases nos histogramas bidimensionais RG-YB são procurados. Picos e pontos base determinam áreas no plano RG-YB. A queda de pixels em uma dessas áreas cria uma região. A queda de pixels em oura área cria outra região. Devido a essa definição permanecem algumas partes não anexadas na imagem. Holla sugere incluir características adicionais como luminance ou a conexão local dos pixels no processo de segmentação para melhorar o resultado.
4.1.5. Segmentação de figuras coloridas com auxílio de informações de cores e vizinhança no espaço
Autor : H.D. vom Stein e W. Reimers([68]).
Ano: 1983.
Definição de região: As montanhas nos histogramas bidimensionais para os pares de cores opostas definem as áreas. A queda dos pixels em uma dessas áreas cria uma região. A queda dos pixels em outra área cria outra região.
Método matemático básico: Achar picos e bases no histograma bidimensional de pares de cores opostas e juntar pixels de acordo com as relações de vizinhança no espaço.
Espaço de Cor: Pares de cores opostas vermelho-verde e amarelo-azul.
Conhecimento Adicional: Nenhum
Aplicação: Propósito Geral.
Descrição: O algoritmo de segmentação
é uma modificação da abordagem de Holla([32]) que
foi descrita na subseção anterior. A modificação
consiste em um processo de refinamento adicional que é empregado
nos resultados de segmentação obtidos com a técnica
de Holla. Se um ou mais pixels na vizinhança 3x3 de um pixel não
indicado são indicados para a mesma região, o pixel é
marcado para indicação para essa região. Nenhuma decisão
é tomada se nenhum dos pixels na vizinhança 3x3 é
indicado ou se muitos pixels na vizinhança 3x3 pertencem a regiões
diferentes. Após toda a imagem ser examinada, os pixels marcados
são indicados para suas correspondentes regiões. Esse procedimento
é aplicado cinco vezes para resultados intermediários. Enquanto
30 a 80 % do pixels são indicados para regiões quando aplica-se
a abordagem de Holla, menos de 10% dos pixels não são indicados
para regiões quando usada essa modificação.
4.1.6. Segmentação de imagens coloridas usando sistema HSI modificado para acompanhamento de estradas
Autor: X. Lin e S. Chen([47])
Ano: 1991
Definição de Região: Duas funções de pertinência de classe baseadas em valores limiares para uma característica escalar V.
Método matemático básico: Segmentação baseada em histograma.
Espaço de cor: HSI modificado, RGB.
Conhecimento Adicional: Dois objetos (estrada e não-estrada).
Aplicação: veículos robóticos
Descrição: Lin e Chen selecionaram o espaço
HSI para acompanhamento de estrada e compararam os resultados com aqueles
computados no espaço RGB. O objetivo da segmentação
para acompanhamento de estradas é dividir uma imagem ao ar livre
em regiões que constituem a estrada ou não. Assume-se que
estradas aparecem luminosas e com baixa saturação e áreas
não-estrada correspondem a baixa intensidade e alta saturação,
Lin e Chen reduziram o processo de segmentação a um problema
de busca unidimensional. Para cada pixel na imagem eles calculam o valor
V = (S – Smédia) – (I – Imédia), onde S representa
a saturação do pixel, I representa a intensidade do
pixel, e Smédia e Imédia são os valores médios
de saturação e intensidade, respectivamente, para a imagem
toda. Os pixels são classificados em áreas de estrada ou
não através de um limite que é determinado pelos picos
no histograma para todos valores V. Nesta investigação, Lin
e Chen constataram que seu algoritmo era mais estável utilizando
os componentes S e I , do que usando o espaço RGB
com o valor V definido como V – (2R – G – B)/(G – B). Isto sustenta-se
quando a imagem contém partes da estrada sombreadas.
4.1.7. Segmentação de imagem colorida usando três atributos perceptuais
Autor : S. Tominaga ([7])
Ano: 1986
Definição de Região: Picos dos três histogramas nos componentes H, V e C do espaço de Munsell determinam os intervalos. A queda dos pixels em um desses intervalos cria uma região. A queda dos pixels em outra área cria uma outra região.
Método matemático básico: Achar picos e bases em histogramas unidimensionais dos três componentes do espaço de Munsell.
Espaço de cor: Tom (hue), Valor (value) e Chroma do espaço de Munsell.
Conhecimento adicional: Nenhum.
Aplicação: Propósito geral.
Descrição: Visto que não existe fórmula analítica para a conversão entre o sistema padrão CIE e o sistema de Munsell, a conversão é baseada em uma tabela ([79]). O algoritmo para segmentação consiste nos seguintes passos:
- Primeiro, a imagem inteira é considerada como uma única região, e os histogramas são computados para cada atributo de H, V e C. Em outros casos, esta computação é feita para as regiões específicas a serem segmentadas. Os histogramas são uniformizados através de um operador de média.
- O pico mais significante é encontrado num grupo de três histogramas. A seleção do pico é baseada na análise da forma de pico no histograma. Primeiro, alguns picos evidentes são selecionados. Depois, a seguinte função de critério é calculada para cada candidato a pico:
- O thresholding de uma imagem colorida é executado usando dois thrsholds derivados do menor limite V1 e do maior, V2, para o pico mais significante no grupo dos três histogramas.. Aqui, uma região de imagem é partida em dois grupos de sub-regiões; uma consiste na sub-região correspondente aos atributos de cores com limites de threshold, e a outra é um grupo de sub-regiões com valores atribuídos restantes.
- O processo de thresholding é repetido para a extração de sub-regiões. Se todos histogramas tornam-se monomodais , a detecção de grupo precisa ser acabada e um rótulo adequado é indicado para as últimas sub-regiões extraídas. A propriedade 8 de conexão é utilizada para uniformizar a imagem rotulada e para eliminar pequenas regiões e linhas curtas.
- Para as regiões restantes, devem ser repetidos os passos de 1 a 4. O processo de segmentação é acabado quando uma área das regiões é suficientemente pequena em comparação ao tamanho da imagem original, ou nenhum histograma possui picos significantes. Os picos restantes, sem rotulação, são unidos na regiões vizinhas de cor similar rotuladas.
![]()
Onde Sp indica a área pico entre dois vales V1 e V2, Fp é a largura cheia na metade do máximo do pico, e Ta indica a área total do histograma, isto é, o numero total de pixels na região de imagem especificada.
4.1.8. Um
método de classificação de cor para imagens coloridas
utilizando o espaço de cor uniforme
Autor: S. Tominaga ([71])
Ano: 1990
Definição de Região: Regiões uniformes são definidas por histogramas de thresholding e de acordo com distâncias mínimas de cor em relação ao centro dos blocos.
Método matemático básico: Três histogramas unidimensionais são analisados para achar picos e vales significantes. Então um processo de reclassificação é empregado, classificando as cores representativas para os blocos extraídos em uma distância de cor.
Espaço de Cor: CIE (Lab)
Conhecimento Adicional: Nenhum
Aplicação: Propósito geral
Descrição: A abordagem consiste de dois passos.
O primeiro é a modificação do algoritmo apresentado
por Tominaga em 1986 (70]) o qual foi descrito na subseção
anterior (4.1.7). A modificação é empregada para resolver
o problema de manipulação de blocos sobrepostos. Esta consiste
em computar os principais eixos componentes no espaço Lab
para todas as regiões a serem segmentadas. A seguir, busca-se picos
e vales em três histogramas unidimensionais de cada eixo coordenado
(como no algoritmo mencionada na subseção anterior). O segundo
passo é suplementado pelo algoritmo para a reclassificação
dos pixels em uma distância de cor. Se um grupo de K cores representativas
{m1, m2, ..., mk} é extraído
da imagem, isto é, a imagem é rotulada por K regiões,
então a reclassificação é aplicada de acordo
com o seguinte esquema: m1 é escolhido como o centro do primeiro
bloco a1 no espaço de cor a1=m1.
A seguir, a diferença de cor de m2 para a1 é computada.
Se esta diferença exceder um certo limiar T, um novo centro de bloco
a2 é criado como a2=m2. Sob outro
aspecto, m2 é designado para o domínio da classe
a1. De uma maneira similar, a diferença de cor a partir
de cada cor representativa (m3, m4, ...) para todos
os centros de blocos estabelecidos é computada e delimitada. Um
novo bloco é criado se todos essas distâncias excederem T,
senão a cor é designada para a classe da qual ela está
mais próxima. Infelizmente, o autor não menciona a medida
da cor que ele utiliza, mas aparentemente qualquer medida de cor seria
conveniente.
4.2.
Agrupamento em espaço de cor
4.2.1 Segmentação de imagem colorida e classificação através de multiedição e condensamento
Autor: F. Ferri e E. Vidal ([18])
Ano: 1992
Definição de região: Pixels são designados para a região específica usando a regra NN. Protótipos para a região são derivados por multiedição seguida de técnica de condensamento.
Método matemático básico: Agrupamento com algoritmo NN. Redução do número de protótipos utilizando multiedição e condensação.
Espaço de cor: YUV
Conhecimentos adicionais: A cena é constituída por folhas, frutas e céu.
Aplicação: Colhedor robótico de cítricos.
Descrição: Um agrupamento supervisionado é realizado em um espaço caracterizado por 10 dimensões e constituído por vetores F característicos baseados nos componentes cromáticos do sistema YUV de cor (14). A saber, com cada pixel (i, j) juntamos o vetor característico:
![]()
O passo h é escolhido em concordância com o tamanho esperado dos pedaços da imagem da fruta, tendo em vista a ótica conhecida e a distância entre a câmera e a cena.
No experimento, duas imagens de treinamento representativo com resolução 128X128 foram manualmente segmentadas e cada região é aleatoriamente subrepresentada de acordo com os objetos menores, ou seja, frutas. Desta forma 1513 grupos de elementos de treinamento foram obtidos (493 para frutas, 644 para folhas, e 376 para céu). No passo da multiedição o número total de protótipos foi 1145 (385 para frutas, 428 para folhas, e 359 para céu). O passo de condensamento trouxe uma redução dramática dos dados para 33 protótipos ( 9 para frutas, 12 para folhas, e 1 para céu) . Em quatro imagens teste, a performance NN alcançou cerca de 90 % de classificação correta de pixels.
Algoritmo de Multiedição
Entrada: Grupo de referência inicial R, número de interações sem modificação IÎ N, número de blocos em cada divisão m > 2.
Saída: Grupo de referência multieditado.
Método:
- Divida aleatoriamente R em m subgrupos R(i), i=1,...,m.
- Para i = 1,...m, classifique referências em R(i) com a regra NN usando R(i mod m+1) como grupo treinamento.
- Descarte aquelas referências que foram mal classificadas no passo 2 e com as restantes forme o novo grupo R.
- Se as últimas iterações I decorrerem sem edição, então PARE, senão VÁ para o passo 1.
Entrada: Grupo R de referência multieditada.
Saída: Grupo S de referência condensada (inicializado em um grupo vazio).
Método:
- Selecione um ponto de referência de R e junte com S.
- Para cada ponto p ÎR classifique p com S como o grupo treinamento, se p é mal classificado então transfira p de R para S.
- Se nenhuma transferência ocorrer durante o passo 2 ou R estiver vazio então PARE, senão vá para o passo 2.
Autor: S.E. Umbaugh, R.H. Moss, W.V. Stoecker, e G.A. Hance ([75]).
Ano: 1993
Definição de região: Os pixels são classificados pela distância mínima em relação aos representativos (protótipos) únicos das classes.
Método matemático básico: Transformação KL no espaço de cor. Subdivisão mediana ao longo do alcance máximo do eixo.
Conhecimento Adicional: O número de regiões segmentadas é conhecido.
Aplicações: Identificação de características de tumor na pele.
Descrição: Representativos são obtidos por meio do processo de ruptura mediana nas coordenadas de transformação KL no espaço de cor. A saber, a cada passo de subdivisão a caixa mais ocupada é escolhida e o eixo com a extensão máxima é tomado e rompido no ponto mediano sobre aquele eixo. A subdivisão é continuada até que o número especificado de caixas é obtido. Então, representativos são tomados como centros de gravidade dos pontos em cada caixa.
Os autores apresentam os melhores resultados de classificação para coordenadas cromáticas, mas a partir do texto podemos apenas entender que uma espécie de rgb (normalizada por intensidade uma combinação linear de coordenadas RGB) foi utilizada.
É interessante que o número de regiões alvo no processo de segmentação não é dado pelo operador, mas oferecido pela máquina de indução de inteligência artificial, que possui regras indutivas baseadas na primeira e segunda instrução das estatísticas RGB. A base de conhecimento foi definida por dermatologistas.
4.2.3. Segmentação de imagens coloridas usando análise recursiva do componente principal e ruptura do vetor mediano.
Autor: W. Skarbek
Ano: * * **
Definição de região: Pixels na região específica estão na lista designada para folhas na árvore mediana. Esta árvore é criada pela ruptura do espaço pelo plano perpendicular na direção da maior variância, indo através do ponto mediano. A ruptura não é continuada se a condição de uniformidade for verdadeira.
Método matemático básico: Análise do componente principal. Método Jacobi para autovetors. Manipulações de árvores binárias.
Espaço de cor: rgb
Conhecimento adicional: nenhum
Aplicação: propósitos gerais
Descrição de região: Antes da especificação do algoritmo, fornecemos a fórmula para a direção e com a variância máxima para um dado grupo de cores, tomado da lista L de pixels. Por variância var ( L, e) queremos designar a variância de projeções sobre a direção e passando através do centro de gravidade das cores em L:
![]()
onde
![]()
A seguir precisamos da seguintes estatísticas:
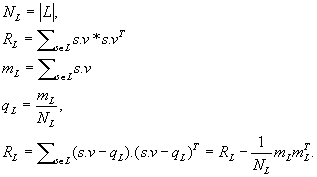 (23)
(23)- Matriz RL é simétrica.
- Direção eL da variância máxima var (L, e) é o autovetor eL da matriz RL correspondendo ao máximo eigenvalue lL.
- Var (L, eL) = lL /NL.
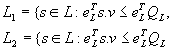 (24)
(24)![]()
para todas características de cores f (aqui f=
r, g, b), onde f(L) indica a média das características
f
no grupo L.
Construção da árvore mediana
- Inicialize a raiz (root) da árvore T e a lista inicial:
- Determine para a raiz (root.L) as estatíticas R, m, N, q;
- Faça até todas a folhas serem marcadas UNIFORME
root.L := todos os pixels na imagem;
- Ache em T, a folha n não marcada UNIFORME tal que ln.L seja o maior
- Subdivida temporariamente n.L em duas listas L1 oraz L2 de acordo com o critério 24. Se os grupos de pixels L, L1 e L2 forem consistentes em cor então cancele esta subdivisão, marque n como UNIFORME e continue do passo 3, caso contrário designe-os para dois nodos filhos de n:
- Determine para n1.L oraz dla n2.L estatísticas R, m, N, q.
n1.L := L1 ; n2.L :=L2 ;
- Para cada folha n em T ache todos componentes conectados no grupo n.L.
Autor: B. Lauterbach e W. Anheier ([45]).
Ano: 1993
Definição de Região: Pixels são classificados por sua distância mínima em relação às linhas de combinação de cores adicionadas, definidas entre cada dois centros de blocos, que são picos nos histogramas uv bidimensionais.
Método Matemático Básico: Seleção de picos em histogramas uv bidimensionais. Construção de linhas de combinação de cores adicionadas e computação da distância geométrica dessas linhas.
Espaço de Cor: CIE (Luv).
Conhecimento Adicional: Os mapas são impressos com letras pretas em um papel branco.
Aplicação: Segmentação de mapas topográficos coloridos.
Descrição: São procurados máximos nos espaços de cor Luv dos histogramas uv cumulativos para definir centros de blocos para segmentação. Os máximos são detectados através da computação das diferenças entre os valores do histograma cumulativo e do valor médio de uma janela circundante. Linhas de combinação de cores adicionadas, são definidas por linhas retas entre dois centros de blocos. Ao invés de classificar pixels pela distância de cor até o centro do bloco, os pixels são classificados par um par de blocos pela distância Euclidiana do valor de pixels até as linhas de combinação de cores adicionadas (acl) entre aqueles dois centros de blocos no espaço uv. Além disso, um círculo é definido ao redor de cada centro de bloco para evitar erro na classificação de um pixel que estiver perto do centro dos blocos. A distância do pixel para o acl deve ser menor do que a distância entre os dois centros de classificação. Depois de todos pixels terem sidos designados para um par de blocos, a classificação final é feita tomando a distância mínima do pixel em relação a um dos dois centros de blocos. Esta segmentação não leva em conta a luminância. Portanto, o bloco monocromático é partido em novos blocos por procura do pico no histograma L unidimensional. Devido ao procedimento anteriormente mencionado, este algoritmo não é uma abordagem genérica para segmentação de imagens coloridas.
4.2.5. Uma técnica de agrupamento recursiva para segmentação de imagens coloridas
Autor: M. Celenk ([13]).
Ano: 1988.
Definição de Região: volumes 3-D no espaço CIE (Lab) determinam a distribuição de cores dos blocos. Pixels com vetores de cor localizados dentro desse volume pertencem a mesma região.
Método Matemático Básico: Detectar blocos adequando à eles alguns volumes de decisão cilíndrico-círcular no espaço CIE (Lab). Determinar limites dos blocos achando picos e vales no histograma 1-D de L, a e b. Então, projetar as distribuições de cores estimadas na função linear Fisher para o thresholding 1-D.
Espaço de cor: CIE (Lab), L*HoC*
Conhecimento adicional: Nenhum
Aplicação: Propósito Geral.
Descrição: A segmentação de imagem colorida é considerada como um problema recursivo de detecção de blocos. O método opera no espaço de cor CIE (Lab) e detecta blocos adequando-os à algum volume de decisão cilíndrico-círcular. Isto estima a distribuição dos blocos no espaço de cor uniforme sem impor qualquer pressão nas suas formas. Os limites dos elementos de decisão consistem em dois planos de luz constante, dois cilindros de cor constante, e dois planos de tom constante. Eles são determinados usando histogramas 1-D das coordenadas L*HoC* no espaço. O espaço de cor psicométrico L*HoC* ou LHC (numa notação curta) é a representação cilíndrica do espaço Lab. É dado por L=L, H=arctan(b/a), e C = (a2 + b2)1/2 (compare as equações (15) e (16)). Os blocos detectados são então isolados dos seus vizinhos pela projeção de suas distribuições de cor estimadas na função discriminante linear Fisher. Para dois blocos de cor w1 e w2 a linha Fisher é dada por W=(K1+ K2)-1(M1-M2), onde (K1,K2) e (M1, M2) são matrizes de covariância e os vetores médios, respectivamente, dos dois blocos. Os vetores de cor dos pontos da imagem, que são os elementos w1 e w2, são então projetados nessa linha dada pela equação acima, usando d(C)=WTC. Aqui, d é a função discriminante linear e C é o vetor de cor em um dos blocos. Um histograma unidimensional é calculado para os pontos de dados projetados, e tresholds são determinados pelos picos e vales do histograma.
4.2.6. Segmentação inicial para indexação de conhecimento
Autor: M.Hild, Y. Shirai, e M. Asada ([31])
Ano: 1992
Definição de Região: As regiões são definidas por 19 blocos de tom dados.
Método Matemático Básico: Projetar previamente pixels de imagem em 19 predefinidos blocos de tom e achar grupos de tom a partir das densidades de pixels nos blocos.
Espaço de cor: HSI.
Conhecimento adicional: Modelo de reflexão dicromático.
Aplicação: Geração de índices em uma base de conhecimento de modelos de objetos.
Descrição: Hild, Shirai, e Asada definem indexação
de conhecimento como o ato de achar peças de conhecimento relevantes
numa base de conhecimento com a ajuda de um grupo de propriedades descritivas,
chamadas índices. Há uma afinidade entre catalogação
e adequação. Enquanto adequação refere-se a
estabelecer correspondências entre um grupo de propriedades de um
modelo carregado, a regra de indexação é estabelecer
conexões para modelos ou partes de modelos sem verificar se essas
conexões são propícias. Dessa forma, um índice
pode ser usado como uma hipótese do objeto representado na imagem.
O processo de segmentação é usado para achar características
relevantes que possam ser usadas como índices numa base de conhecimento.
Obviamente, a cor não é a única característica
possível numa base de conhecimento, mas é uma característica
importante. Visto que histogramas de tom, saturação, e intensidade
são freqüentemente ambíguos eles não são
adequados para uma discriminação suficiente de objetos a
serem segmentados em imagens similares. Os autores propõem dividir
o espaço do tom em 19 partições diferentes. Então,
as imagens são previamente projetadas nessas partições
e a densidade do pixel é calculada em cada uma das partições.
Os blocos de tom são agrupados de acordo com essas densidades para
definir características cromáticas que podem ser usadas como
índice na base de conhecimento.
4.3.
Agrupamentos fuzzy no espaço de cor
4.3.1 Algoritmo de segmentação de imagens coloridas baseado nas técnicas de thresholding e fuzzy c-means
Autor : Y.W.Lim e S.U.Lee([46]).
Ano: 1990
Definição de Região: Pixel é alocado para a região usando a função de associação fuzzy dos máximos. Entretanto, para uma segmentação rudimentar, a maioria dos pixels já está designado para regiões usando os limites do hexahedra
Método Matemático Básico: Análise do espaço escalar do histograma. Agrupamento fuzzy c-means.
Espaço de cor: RGB, XYZ, YIQ, Luv, I1I2I3 (definido no trabalho de Ohta [53]).
Conhecimento adicional: Nenhum.
Aplicação: Propósito geral
Descrição: Visto que o número de regiões é desconhecido, uma segmentação rudimentar é feita através da análise do espaço escalar de histogramas 1-D. Esta análise habilita uma confiável detecção de picos significativos no histograma dado e ao mesmo tempo determina intervalos significantes ao redor desses picos. Os limites dos intervalos são achados como cruzamentos-zero da segunda derivada para a versão t -escalar no histograma. Os parâmetros escalares adequados seguem a árvore de intervalo de Witkin com o diagrama de fingerprint.
A t -escalar do histograma h(x) é definida pela convolução de h com a função Gaussiana que tem média zero e desvio padrão igual a t :
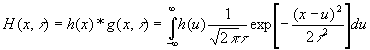
A Segunda derivada da função escalar pode ser computada pela convolução com a segunda derivada da função Gaussiana:
![]()
A segmentação rudimentar produz um número de hexahedra obtidos como produtos cartesianos dos intervalos de picos achados para cada componente de cor separadamente. Os pixels não entrando nos hexahedras entram nas regiões ambíguas. O refinamento dessa segmentação é feito com agrupamento através de fuzzy c-means. Os centros de gravidade dos pixels no hexahedra são usados inicialmente como representações das classes fuzzy.
Algoritmo de segmentação rudimentar
- Compute histogramas para cada componente de cor na imagem;
- Aplique a análise do espaço escalar para os histogramas;
- Defina classes validas (hexahedra) V1,..., Vc;
- Para cada pixel p, Se pertence a um dos hexahedra Vi, então p é classificado e rotulado por i, caso contrário, ele não é classificado;
- Calcule o centro de gravidade vi para cada classe Vi.
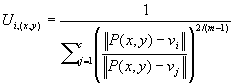
A constante m controla o processo de agrupamento. Tipicamente m =2.
O pixel (x,y) é associado a classe Vk tal que o seu valor de pertinência é máximo:
![]()
4.3.2 Segmentação fuzzy interativa de imagem
Autor: T.L. Huntsberger, C.L. Jacobs e R.L.Cannon ([37])
Ano: 1985
Definição de região: regiões são criadas por pixels que têm seu valor de pertinência fuzzy acima do corte-a .
Método matemático básico: Algoritmo fuzzy c-means
Espaço de cor: RGB, I1I2I3.
Conhecimentos adicionais: nenhum
Aplicação: propósito geral
Descrição: Esta abordagem é completamente baseada no algoritmo original de Bezdek ([9]) para agrupamentos fuzzy. No estágio consecutivo o procedimento de agrupamento é aplicado para os pixels restantes não classificados. Para cada pixel ele elabora a função de pertinência fuzzy e uma vez que seu valor máximo satisfaz o corte-a , o pixel é classificado.
Algoritmo fuzzy c-means
Para os dados de pontos fornecidos x1, ..., xnÎRp :
- Fixe c, 2 £ c<n; escolha qualquer norma métrica de produto interno para Rp ; e fixe m, 1 £ m < ¥ . Inicialize (por exemplo: uniformemente) a função de pertinência U0: {1, ..., m} X {1, ..., c} ® [0, 1]. Então, no passo l =0, 1, 2,...:
- Calcule c centro do bloco fuzzy {vi(l)}:
- Atualize U(l): Deixe dik= || xk – vi||:
- Compare U(l) à U(l+1): se ||U(l+1) – U(l)||£Î então PARE, senão Vá para o passo 2
![]() /
/ ![]()
Se dik ¹ 0 então 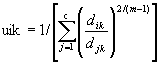 senão uik = 0.
senão uik = 0.
Podem ocorrer dois centros de blocos são muito próximos, então é melhor uni-los em um só bloco. Os autores usaram a seguinte relação de equivalência para os centros de blocos:
para cada característica de cor ![]()
4.3.3 Segmentação de baixo nível de imagens aéreas com agrupamento fuzzy
Autor: M. Trivedi e J.C. Bezdek ([73]).
Ano: 1986
Definição de região: regiões são criadas por pixels que possuem seu valor de pertinência fuzzy acima do corte-a .
Método matemático básico: Algoritmo fuzzy c-means
Espaço de cor: Espaço multiespectral ( por exemplo: os canais de imagens LANDSAT)
Conhecimentos adicionais: nenhum
Aplicação: segmentação de imagens multiespectrais.
Descrição: Esta abordagem é baseada no algoritmo de Bezdek ([9]) para agrupamentos fuzzy. Logo, o algoritmo é idêntico ao algoritmo fuzzy c-means empregado por Huntsberger, Jacobs e Cannon ([37]) o qual foi descrito na subseção anterior. A diferença entre as duas abordagens é que Trivedi e Bezdek implementaram seu algoritmo em uma estrutura pirâmide de dados. Quatro valores são substituídos pelo seu valor médio para construir um nível mais alto na pirâmide. Começando pelo nível mais alto, as regiões são criadas por pixels que têm seu valor de pertinência fuzzy acima do corte-a . Para aquelas áreas na imagem que não são homogêneas devido à definição mencionada acima, a pertinência fuzzy é checada no segundo nível da pirâmide.
Contato:
Tel.: +55-48-331 7552/9498 |



