Main features of SCG

Let be a vector from the space , where N is the sum of the number of weights and of the number of biases of the network. Let E be the error function we want to minimize.

SCG differs from other CGMs in two points:

• each iteration k of a CGM computes , where is a new conjugate direction, and is the size of the step in this direction. Actually is a function of , the Hessian matrix of the error function, namely the matrix of the second derivatives. In contrast to other CGMs which avoid the complex computation of the Hessian and approximate with a time-consuming line search procedure, SCG makes the following simple approximation of the term , a key component of the computation of :

  

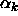• as the Hessian is not always positive definite, which prevents the algorithm from achieving good performance, SCG uses a scalar which is supposed to regulate the indefiniteness of the Hessian. This is a kind of Levenberg-Marquardt method [P88], and is done by setting:

  

  and adjusting at each iteration. This is the main contribution of SCG to both fields of neural learning and optimization theory.

SCG has been shown to be considerably faster than standard backpropagation and than other CGMs [Mol93].