
Visão Computacional
1. Representação de
imagens
2. Filtragem de imagens
3. Detecção de Bordas
4. Segmentação Simples
5. Crescimento de Regiões
6. Segmentação com
Filtros
7. Segmentação a Cores
8. Análise de Texturas
9. Análise de Texturas
Multiescalar
10. Redes Neurais
11. Morfologia Matemática
12. Convolução
13. Esqueletonização
14. Técnicas Estatísticas
15. Fractais
16. Reconhecimento de
Formas
17. Representação de
Objetos
18. Quadtrees e Octrees
19. Visão Estereo
20. Inteligência Artificial
21. Controle de qualidade
22. Robótica
23. Medicina
24. Sensoriamento remoto
Prof. Aldo von Wangenheim
Currículo...
Publicações
Pesquisa
Projetos
Ensino de Graduação
Ensino de Pós Graduação
Cursos
Morfologia Matemática
Alexandre Orth
Florianópolis, 4 de Setembro de 2000.
Neste trabalho,
apresentaremos de uma forma geral a metodologia da morfologia matemática
aplicada a visão computacional. As definições básicas
da técnica são apresentadas, em seguida de exemplos e propriedades.
Os operadores morfológicos básicos são apresentados
e as suas variações mais importante. Analisa-se também
a questão da esqueletonização usando-se operadores
morfológicos e a questão da aplicação deste
operadores em imagens de tons de cinza.
- Introdução
- DEFINIÇÃO DE MORFOLOGIA
- Definição de Imagem Binária
- Definições Fundamentais
- Dilatação e Erosão
- Exemplo de Dilatação
- Exemplo de Erosão
- Propriedades da Dilatação e Erosão
- Convolução Booleana
- Abertura e Fechamento
- Exemplos de Abertura
- Exemplos de Fechamento
- Acerto e Erro (Hit and Miss)
- Aplicações das Operações Básicas
- Esqueletonização
Morfologia é a forma e estrutura de um objeto ou os arranjos e inter-relacionamentos entre as partes de um objeto.
Os mais antigos usos desta palavra estão relacionados com linguagem e biologia. Em lingüística, morfologia é o estudo da estrutura das palavras. Em biologia, morfologia esta relacionada mais diretamente a forma de um organismo. A forma de uma folha pode ser usada para identificar uma planta ou a forma de uma colônia de bactérias pode ser usada para identificar sua variedade.
Morfologia digital é um caminho para descrever ou analisar a forma de um objeto digital.
A morfologia digital é uma ciência relativamente recente, pois só os computadores digitais permitiram seu uso na pratica. Por outro lado os matemáticos a consideram uso da teoria de conjuntos que é uma area bem estudada.
A idéia de morfologia digital é que uma imagem consiste de um conjunto de "picture elements" (pixels) que são reunidos em grupos tendo uma estrutura bidimensional (forma).
Certas operações matemáticas em conjuntos de pixels podem ser usadas para ressaltar aspectos específicos das formas permitindo que sejam contadas ou reconhecidas.
As operações básicas da morfologia digital são a erosão, em que pixels que não atendem a um dado padrão são apagados da imagem, e dilatação, em que uma pequena area relacionada a um pixel é alterada para um dado padrão. Todavia, dependendo do tipo de imagem sendo processada (preto e banco, tons de cinza ou colorida) a definição destas operações muda, assim cada tipo deve ser considerado separadamente.
Uma imagem pode ser definida, de forma alternativa, como um conjuntos de coordenadas (x,y) pertencentes a esta imagem, tanto no campo contínuo como no campo discreto. No sentido que esta conjunto corresponda aos pontos ou pixels pertencentes ao objeto da imagem. Esta idéia é visualizada na Fig. 1.1, onde têm-se dois objetos ou conjuntos de pixels A e B. Note a utilização do sistema de coordenadas (n, m). Neste momento, iremos considerar que os valores que os pixels podem assumir são binários, ou seja, cada pixel ou contém valor 0 ou contem valor 1. Desta forma, podem-se restringir esta análise para o espaço discreto Z2. Mais tarde, trataremos de imagens com tons variáveis de cinza.
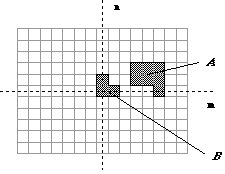
Fig. .1 : Uma imagem binária contendo 2 objetos (i.e. 2 conjuntos de pontos).
O objeto A consiste dos pontos a que possuem pelo menos uma propriedade em comum:
Objeto: ![]()
Como exemplo,
o objeto Bna Fig. 1.1 consiste de ![]() .
.
O fundo da imagem de A, denominado AC (o complemento de A), consiste dos pontos que não pertencem ao objeto A:
Fundo: ![]()
As operações
fundamentais associadas com um objeto são o conjunto padrão
de operações:
união![]() ,
interseção
,
interseção![]() ,
e complemento
,
e complemento![]() com translação:
com translação:
Translação: Dado um vetor x e um conjunto A, a translação, A + x, é definida como:
Translação: ![]()
Note que, como estamos tratando com imagens digitais compostas de pontos com coordenadas inteiras (Z2), isto implica em restrições no vector de translação x.
O conjunto básico de operações de Minkowski adição e subtração podem agora ser definidos, baseado nas considerações anteriores. Dados dois conjuntos A e B:
Adição
de Minkowski: ![]()
Subtração
de Minkowski: ![]()
A partir das operações básicas de Minkowski, pode-se definir as operações básicas da morfologia matemática, dilatação e erosão:
Dilatação: ![]()
Erosão: ![]()
onde ![]() .
Estes dois operações foram aplicadas nos objetos da Fig.
1.1 e os resultados estão apresentadas Fig. 1.1.
.
Estes dois operações foram aplicadas nos objetos da Fig.
1.1 e os resultados estão apresentadas Fig. 1.1.
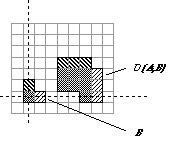
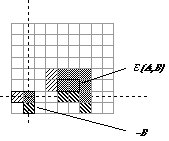
Tanto o conjunto A como o conjunto B podem ser considerados como sendo uma imagem, entretanto A é usualmente considerado com sendo a imagem a ser analisada e B como o elemento estruturante. O elemento estruturante está para a morfologia como o núcleo de convolução (kernel) está para teoria de filtragem linear.
A dilatação, em geral, faz com que o objeto dilate e cresça no tamanho; enquanto que a erosão faz com que o objeto encolha. O modo e a proporção (magnitude) da expansão ou redução da imagem dependem necessariamente do elemento estruturante B. Aplicar uma dilatação ou erosão numa imagem sem especificar um elemento estruturante, não causará nenhum efeito nesta. Os dois elementos estruturantes mais comuns (olhando num plano cartesiano) são os conjuntos 4-conexões e 8-conexões, N4 e N8.
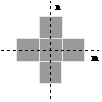
Fig. .2 : Os elementos estruturantes padrão N4 e N8, respectivamente.
A = {(1,1),(1,2),(2,1),(2,2)}= B = {(0,0),(1,0)} =
Para este caso a equação pode ser rescrita como:
A Å B = [A+ {(0,0)}] È [A + {(1,0)}]
A + {(0,0)} = {(1,1),(1,2),(2,1),(2,2)} =
(1,1) + (0,0) = (1,1)
(1,2) + (0,0) = (1,2)
(2,1) + (0,0) = (2,1)
(2,2) + (0,0) = (2,2)
A translação de qualquer pixel por (0,0) não altera sua posição.
A + {(1,0)} = {(2,1),(2,2),(3,1),(3,2)} =
(1,1) + (1,0) = (2,1)
(1,2) + (1,0) = (2,2)
(2,1) + (1,0) = (3,1)
(2,2) + (1,0) = (3,2)
AÅ
B = {(1,1),(1,2),(2,1),(2,2),(3,1),(3,2)} =
O pixel marcado com um "x" representa a origem (0,0) de cada imagem. A localização da origem é muito importante; No exemplo anterior se a origem do conjunto B fosse o pixel da direita, {(-1,0),(0,0)}, a dilatação acrescentaria pixels a esquerda na imagem A.
O conjunto A q B é o conjunto de translações de B que alinham B sobre o conjunto de pixels pretos em A. Isso Significa que nem todas as translações necessitam ser consideradas, mas somente aquelas que inicialmente localizam sua origem de B em um membro de A. Existem 4 dessas translações:
B(1,1) = {(1,1),(2,1)}
Como os pixels (1,1) e (2,1) são pretos na imagem A.
O pixel (1,1) no resultado será preto.
B(1,2) =
{(1,2),(2,2)}
Como os pixels (1,2) e (2,2) são pretos na imagem A.
O pixel (1,2) no resultado será preto.
B(2,1) =
{(2,1),(3,1)}
Como o pixel (3,1) não é pretos na imagem A.
O pixel (2,1) no resultado não será preto.
B(4,4) = {(4,4),(5,4)}
Como o pixel (5,4) não é pretos na imagem A.
O pixel (4,4) no resultado não será preto.
A q B = { (1,1) | B(1,1) ÍA} È { (1,2) | B(1,2) ÍA}
A dilatação e a erosão possuem as seguintes propriedades:
Comutatividade: ![]()
Não-Comutatividade: ![]()
Associatividade: ![]()
Invariante
de Translação: ![]()
Dualidade: 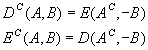
Considerando A como um objeto e AC como o seu fundo (complemento), esta equação afirma que a dilatação de um objeto é igual a erosão aplicada ao seu fundo. Da mesma maneira, a erosão de um objeto é gera o mesmo resultado que a dilatação do seu fundo.
Exceto em casos especiais:
Não-Inversos:![]()
A erosão possue a seguinte propriedade de translação:
Invariante de
Translação: ![]()
A dilatação
e a erosão possuem a seguinte propriedade importante. Para qualquer
elemento estruturante arbitrário B e dois objetos A1
e A2 de modo que ![]() (i.e.,
A1é um subconjunto de A2):
(i.e.,
A1é um subconjunto de A2):
Crescimento
em A: ![]()
Para 2 elementos
estruturantes B1 e B2, de modo que ![]() :
:
Decréscimo
em B: ![]()
O teoremas da decomposição abaixo permitem a implementação de algoritmos eficientes para a filtragem morfológica:
Dilatação: ![]()
Erosão: ![]()
Erosão: ![]()
Dilatações
Múltiplas: ![]()
Um importante teorema de decomposição é o teorema de Vincent. Primeiramente, precisamos de algumas definições. Um conjunto convexo (no R2) é um conjunto onde qualquer linha reta que ligue quaisquer dois pontos do conjunto, conterá somente (i.e. passará necessariamente por) pontos pertencentes a este conjunto. Precisamos tomar cuidado ao considerar esta questão no plano discreto, haja visto que o conceito "linha reta" precisa ser considerado apropriadamente para o problema em Z2. Um conjunto é limitado, se cada um dos seus elementos tem uma magnitude finita, neste caso a distância até a origem no plano de coordenadas. Um conjunto é simétrico, se B = -B. Os conjuntos N4 e N8 apresentados na Fig. 1.2 são exemplos de conjuntos convexos, limitados e simétricos.
O teorema de
Vicent quando aplicado a uma imagem contendo pixels (pontos) discretos,
afirma que para um elemento estruturante limitado, simétrico, que
não contém buracos (i.e. contém todos os pontos no
interior do seu contorno) e contém o seu próprio centro, ![]() :
:
![]()
onde ¶ A é o contorno do objeto. Isto é, ¶ A é um conjunto de pixels que possui pelo menos um pixel pertencente ao fundo como seu vizinho.
A implicação deste teorema é que não é necessário processar todos os pontos pertencentes a um objeto para calcular a sua dilatação e/ou a sua erosão, basta processar os pontos pertencentes ao contorno do objeto. Isto também se aplica a todas as operações derivadas da dilatação e da erosão. Isto implica em uma grande redução na complexidade computacional reduzida de O(N2) para O(N) para uma imagem NxN. Muitos algoritmos velozes podem ser obtidos na literatura que empregam esta técnica. Os mais simples algoritmos de dilatação e erosão são frequetementes descritos da seguinte forma:
Dilatação: Pegue cada pixel binário do objeto (com valor 1) e mude todos os pixels do fundo (com valor 0) que estão C-conectados a este para o valor 1.
Erosão: Pegue cada pixel binário do objeto (com valor 1) que estão C-conectados aos pixels do fundo (com valor 0) e mude para o valor 0.
Comparando-se estes dois procedimento as equações onde B = N4 ou N8 mostra que estes são equivalentes as métodos formais da definição da dilatação e erosão.
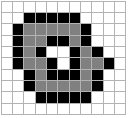 B = N4
B = N4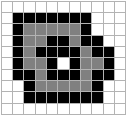 B = N8
B = N8
Fig. .1 : Exemplo de dilatação. Pixels originais em cinza e pixels adicionados em preto.
Uma imagem binária
arbitrária (ou elemento estruturante) A pode ser representado como: ![]()
onde S e ´ são as operações booleanas OU e E respectivamente, a[j,k] é a função característica que pode assumir valores booleanos da seguinte forma:
![]()
e ¶ [m,n] é a versão booleana da função delta de Dirac que possui a seguinte definição:
![]()
![]()
A dilatação pode então ser definida para imagens binárias da seguinte forma:
![]()
e como os operadores E e OU são comutativos, pode-se ainda definir da seguinte maneira:
![]()
Usando o teorema de Morgan:
![]() ou
ou ![]()
a erosão pode ser definida como:
![]()
Desta maneira, a dilatação e erosão de imagens binárias pode ser vistas como convoluções sobre a álgebra booleana. Quando aplicamos esta convolução, deve-se adotar ou que todos os pontos fora da imagem binária são 0 ou 1, para que este princípio seja corretamente aplicado.
Pode-se ainda combinar a dilatação com a erosão para construir dois operadores mais importantes:
Abertura: ![]()
Fechamento: ![]()
A abertura e o fechamento possuem as seguintes propriedades:
Dualidade: 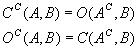
Translação: ![]()
Para a abertura com um elemento estruturante B e as imagens A, A1 e A2, onde A1 é uma sub-imagem de A2 (A1 ÍA2):
Antiextensividade: ![]()
Monotonicidade
Crescente: ![]()
Potência
Idêntica: ![]()
Para o fechamento com um elemento estruturante B e as imagens A, A1 e A2, onde A1 é uma sub-imagem de A2 (A1 ÍA2):
Extensividade: ![]()
Monotonicidade
Crescente: ![]()
Potência
Idêntica: ![]()
Abaixo, apresenta-se
um exemplo básico da técnica de abertura, realizado passo
a passo.
A = B = A q
B = (A q B) Å
B =
Na Fig. 1.1 temos
um exemplo de abertura utilizando-se como elemento estruturante um disco.
A linha pontilhada mais escura apresenta esta resultado e na linha pontilhada
interna temos o resultado de uma erosão aplica após a abertura
com o mesmo elemento estruturante. Na Fig. 1.2 apresentamos outro exemplo
de abertura com um elemento estruturante específico.
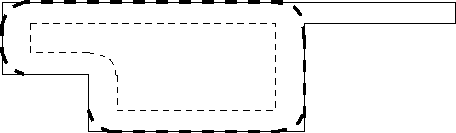
Fig. .1 : Exemplo de abertura (liha pontilhada escura) de A.
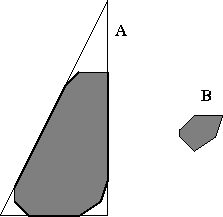
A = B = A Å
B = (A Å B)
q
B =
Na Fig. 1.1 temos um exemplo do fechamento de um objeto através de um elemento estruturante na forma de disco. Em linha normal, define-se o objeto apresentado na imagem. Em pontilhado escuro temos o resultado do fechamento realizado. Em pontilhado claro, o resultado da aplicação de uma dilatação em cima do resultado obtido no fechamento.
O operador Acerto e Erro foi definido por Serra e a sua definição é apresentada abaixo:
Dada uma imagem A e dois elementos estruturantes B1 e B2, a definição do operador em diferentes formas:
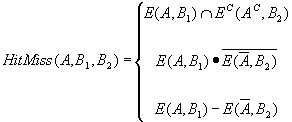
onde B1 e B2 são elementos estruturantes limitados e disjuntos. Dois conjuntos são disjuntos quando B1 ÇB2 = Æ , o conjunto vazio.
Vários elementos estruturantes empregados estão definidos na Fig. 1.1. O valor - indica que não importa o valor assumido (0 ou 1). Todas os três elementos estruturantes são simétricos:
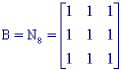
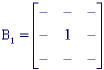
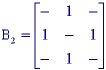
Fig. .1 : Elementos estruturantes B, B1 e B2, todos 3x3 e simétricos.
O resultado do processamento está apresentado nas Fig. 1.2 e Fig. 1.3 (0:branco, 1:preto):


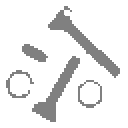
Fig. .2 : a) Imagem A b)Dilatação de A com 2B c) Erosão de A com 2B



Fig. .3 : a) Abertura de A com 2B. b) Fechamento de A com 2B. c) Acerto e Erro com B1 e B2.
A operação de abertura pode separar objeto que estão conectados numa imagem binária. Já a operação de fechamento pode preencher pequenos buracos presentes em uma imagem. Ambas as operações suavizam de certa forma o contorno do objeto.
O operador acerto e erro (Hit and Miss) achou os pixels do contorno que estão 4-conectados. Um método alternativo para obtenção de contornos é aplicar a seguinte relação:
Contorno 4-Conectado: ![]()
Contorno 8-Conectado: ![]()
- Largura da linha: um pixel;
- Passa pelo "meio" do objeto;
- Preserva a topologia do objeto.


No primeiro exemplo, não podemos gerar uma linha que tenha largura de um pixel e passe pelo centro do objeto. Já no outro exemplo, não podemos equeletonizar a imagem preservando a sua topologia, i.e. a noção de conectividade do objeto. Entretanto, existem várias técnicas que auxiliam a obtenção da equeletonização de objetos, quando isto é possível.
Uma forma básica é baseada no trabalho de Lantuéjoul. O subconjunto skeleton Sk(A) é definido como:
Subconjuntos
Skeleton: ![]()
onde K é o maior valor de k antes do conjunto Sk(A) se tornar vazio. O elemento estruturante B é escolhido (em Z2) com uma forma similar a um disco circular, sendo, portanto, convexo, limitado e simétrico. O esqueleto será o resultado da união de um grupo de subconjuntos skeleton:
Esqueleto: ![]()
Um efeito resultante importante desta análise é que a imagem original pode ser reconstruída fornecendo-se os subconjuntos skeleton Sk(A), o elemento estruturante B, e K:
Reconstrução
da Imagem: ![]()
Este método de cálculo do esqueleto da imagem, entretanto, não preserva a sua topologia, não atendendo, portanto, um dos requisitos desejados.
Um método alternativo é implementar um afinador (thinning), uma erosão que reduza um objeto sem perder as suas características morfológicas. Um algoritmo genérico de afinamento é baseado na operação acerto e erro (Hit and Miss):
Afinador (Thinning
): ![]()
Dependendo da escolha de B1 e B2 , uma larga variedade de algoritmos de afinamento podem ser implementadas e, aplicando-se várias vezes estes algoritmos pode-se reduzir uma imagem até o seu esqueleto.
Um método mais prático de afinamento pode ser implementado. Se restringirmos a análise para uma vizinhança de 3x3, similar ao um elemento estruturante B = N8 (Ver Fig. 1.1a), então podemos analisar a operação de afinamento como uma janela que repetidamente varre a imagem binária e mude o seu pixel central para 0 sob certas condições. O ponto central da matriz somente não será modificado para 0 se um dos seguintes casos ocorrer:
- Um ponto isolado foi encontrado.
- Removendo-se este pixel, estaremos alterando a conectividade da imagem.
- Removendo-se este pixel, estaremos reduzindo uma linha.
![]()
![]()
![]()
Fig. .2 : Condições de teste: a)Pixel isolado, b) Pixel conectado a outros, c) Pixel no final de uma linha.
Se somente a condição 1 for considerada, cada objeto na imagem será reduzido a um único ponto. Isto pode ser útil se desejamos contar o número de objetos em uma imagem. Se somente a condição 2 for usada então detectaremos buracos existentes na imagem. Se as condições 1 e 2 forem usadas, cada objeto será reduzido a ou um único pixel, se o objeto não contém furos, ou a um círculo fechado se este contiver furos. Se as condições 1,2 e 3 forem usadas, então um esqueleto complexo será gerado.
Na Fig. 2.3 apresenta-se um exemplo do resultado do emprego desta técnica.
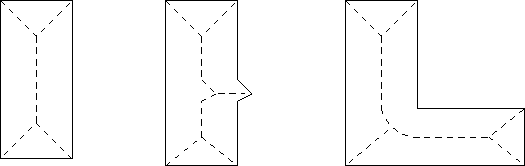
- Propagação
- Aplicação da Esqueletonização e da Propagação
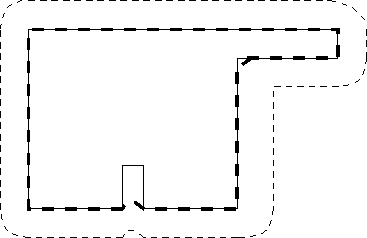
Em muitos casos é conveniente estar apto a reconstruir imagens que sobreviveram a várias erosões ou se preencher um objeto que está definido apenas pela seu contorno (Ver Fig. 2.1). Os mecanismos formais que fazem isto possuem diferentes nomes como: preenchedor de regiões, reconstrução e propagação. A definição formal é dada pelo seguinte algoritmo. Inicia-se com uma imagem semente S(0), uma máscara A, e um elemento estruturante B. Emprega-se então dilatações de S com o elemento estruturante B e a máscara A, de forma interativa, como apresentado a seguir:
Iteração
k: ![]() até:
até: ![]()
A cada iteração a imagem semente irá crescer (através da dilatação) porém sendo limitada pelo conjunto definido por A, i.e. S irá crescer até preencher A. As escolhas mais comuns para B são N4 e N8. Entretanto, o custo de computacional desta operação é extremamente alto, i.e. O(N3). Felizmente, existe um método interativo mais eficiente que necessita de somente 2 ou 3 passos, com complexidade N2.
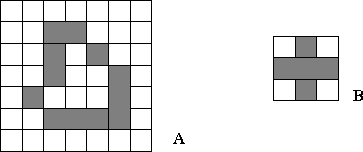
Fig. .1 : A região A é preechinda utilizado-se o elemento estruturante B.
A imagem original (Fig. 2.1a) foi erodida por E(A,6N8) para produzir a semente apresentada em preto na Fig. 2.1b. A imagem original foi usado como mascara para produzir o resultado final da propagação. A operação de propagação é apresentada na Fig. 2.2c.


Fig. .1: a) Imagem original. b) Semente marcada na imagem original nos pixels pretos.
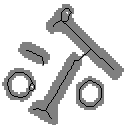

Fig. .2: a) Esqueleto (preto) com pontos finais b) Esqueleto sem pontos finais c) Propagação com N8.
- Morfologia de Imagens em Tons de Cinza
As técnicas de morfologia matemática podem ser aplicadas também a imagens de tons de cinza. Para simplificar as considerações, adotaremos elementos estruturantes B, com um número finito de elementos e que são complexos e limitados. Agora, entretanto, o elemento estruturante possui níveis de cinza associado a cada coordenada como uma imagem em tons de cinza normal.
Para um dada coordenada de saída [m,n], o elemento estruturante é somado com uma versão deslocada da imagem e o máximo valor obtido no domíno J x K de B é usado como resultado. Deve-se considerar um valor definido para os valores dos pixels fora da imagem, geralmente igual ao valor de fundo da imagem.
A dilatação em imagens de tons de cinza pode ser calculada como:
(A Å B) = max {A(i x , j y) + B(x , y) | (i x , j y) Î A , (x, y) Î B}
onde B é um elemento estrutural e A é a imagem de tons de cinza. Para calcular a dilatação faz-se o seguinte:
- Posiciona-se a origem do elemento estrutural sobre o primeiro pixel da imagem a ser dilatada.
- Calcula-se a soma de cada par correspondente de valores de pixels do elemento estrutural e da imagem.
- Acha-se o valor máximo de todas essas somas, e armazena-se o pixel correspondente na imagem de saída para este valor.
- Repete-se este processo para cada pixel da imagem a ser dilatada.
- Valores negativos podem ser alterados para zero (underflow).
- A imagem inteira poderia ter seus valores aumentados para que o menor valor de pixel fosse zero mantendo os valores relativos entre os pixels.
A Erosão em imagens de tons de cinza pode ser calculada como:
(A q B) = min {A(i x , j y) B(x , y) | (i x , j y) Î A , (x, y) Î B}
onde B é um elemento estrutural e A é a imagem de tons de cinza. Para calcular a erosão faz-se o seguinte:
- Posiciona-se a origem do elemento estrutural sobre o primeiro pixel da imagem que sofre erosão.
- Calcula-se a diferença de cada par correspondente de valores de pixels do elemento estrutural e da imagem.
- Acha-se o valor mínimo de todas essas diferenças, e armazena-se o pixel correspondente na imagem de saída para este valor.
- Repete-se este processo para cada pixel da imagem que sofre erosão.
- Propriedades da Dilatação e da Erosão em Tons de Cinza
- Suavização Morfológica
- Gradiente Morfológico
- Laplaciano Morfológico
- Aplicações dos Filtros Morfológicos
A dualidade entre a erosão e a dilatação em imagens de tons de cinza são um pouco mais complexa que nas imagens binárias:
Dualidade: ![]()
onde Ã
significa ![]() .
.
As definições das operações de nível mais alto como abertura e fechamento são:
Abertura: ![]()
Fechamento: ![]()
O processo de abertura funciona da mesma forma que definido anteriormente só que usa dilatação e erosão de tons de cinza. Isto é, a abertura usa uma erosão de tons de cinza seguida de uma dilatação de tons de cinza usando o mesmo elemento estrutural.
O processo de fechamento também funciona da mesma forma que definido anteriormente só que usa agora dilatação e erosão de tons de cinza. Isto é, o fechamento usa uma dilatação de tons de cinza seguida de uma erosão de tons de cinza usando o mesmo elemento estrutural.
As propriedades importantes apresentadas anteriormente como potência idêntica, translação, invariância e crescimento em A, também são aplicáveis no caso da morfologia de tons de cinza.
Em muitos situações a complexidade da morfologia de tons de cinza pode ser radicalmente reduzida através da adoção de elementos estruturantes simétricos, onde b[j,k]=b[-j,-k]. O mais comum deste caso é baseado no uso de B = constante = 0. Para este caso especial e considerando novamente o domínio [j,k]Ì B, as definições acima podem ser reduzidas para:
Dilatação: ![]()
Erosão: ![]()
Abertura: ![]()
Fechamento: ![]()
Exemplos destas operações aplicadas a um sinal simples de uma dimensão é apresentado abaixo:
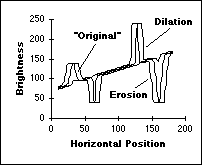
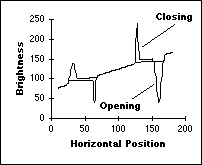
Fig. .1 : a) Efeito da dilatação e erosão 15 x 1. b) Efeito da abertura e fechamento 15 x 1.
Para uma janela retangular J x K, os filtros bidimensionais de máximo e mínimo podem ser separados em dois filtros unidimensionais. Além disso, um filtro unidimensional pode ser escrito em uma forma incremental. Por causa disto, a dilatação e a erosão em tons de cinza possuem uma complexidade constante O(constante), independente de J x K.
Os operadores
apresentados acima podem ser usados para produzir algoritmos morfológicos
como suavização, determinação do gradiente
e Laplaciano. Todos são obtidos a partir das primitivas da erosão
e dilatação em tons de cinza e no casos dos filtros de máximo
e mínimo no domínio ![]() .
.
Este algoritmo é baseado na observação que uma abertura em tons de cinza suaviza uma imagem em tons de cinza. Sua definição é dada por, considerando o elemento morfológico apresentado anteriormente:
![]()
Para filtros não lineares, o gradiente fornece um vetor com uma magnitude e direção. A versão apresentada aqui gera uma aproximação morfológica da magnitude do gradiente:
![]()
O filtro morfológico Laplaciano é definido por:
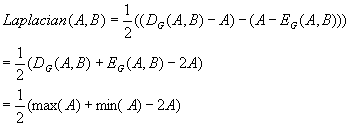



Fig.
.1: a) Dilatação b) Erosão c) Suavização


- "CVonline: Image Transformations and Filters", http://www.dai.ed.ac.uk/CVonline/transf.htm
- "Image Processing Fundamentals", http://www.ph.tn.tudelft.nl/Courses/FIP/noframes/fip-Contents.html
- "Image Processing Resource List", http://www.ncc.com/cdroms/ipt/ipt_sites.html
- "SDC Morphology Toolbox for MATLAB 5", http://www.mmorph.com/
- Cleiton: "Morfologia", Seminário de Visão Computacional, 1998.
- GOMES, Jonas & VELHO, Luiz.: "Computação Gráfica: Imagem." Rio de Janeiro, IMPA/SBM, 1994.
- GONZALEZ, Rafael C. & WOODS, Richard E.. "Digital Image Processing." Reading, Addison-Wesley ,1992.
- Haralick, Robert M. & Shapiro, Linda G. :"Computer and Robot Vision", Addison-Wesley, 1992.
- http://cobb.ece.psu.edu/projects/interact/morphology.html
- PARKER, J. R.. "Algorithms for Image Processing and Computer Vision." New York, John wiley & Sons, 1997.
- RUSS, John C. . "The image processing handbook." 2 ed., Boca Raton, CRC Press, 1995.
- Simon, Greg & Chatterjee, Manu:"Introduction to Morphology", Penn State University, Electrical Engineering, http://cobb.ee.psu.edu/users/greg/morphology.html
- Stapleton, Joe & Mirmehdi, Majid.: "A Java Teaching Aid for Image Morphology", Department of Computer Science, University of Bristol,
http://www.cs.bris.ac.uk/~majid/mengine/morph.html#intro
Contato:
Tel.: +55-48-331 7552/9498 |



