Informações

Curriculo...

Publicações

Pesquisa

Projetos

Ensino de Graduação

Ensino de Pós Graduação 

Visão Computacional

Cursos

Você lê?

Este texto no formato Word 97

DEFINIÇÃO DE MORFOLOGIA

Morfologia é a forma e estrutura de um objeto ou os arranjos e inter-relacionamentos entre as partes de um objeto.

Os mais antigos usos desta palavra estão relacionados com linguagem e biologia. Em lingüística, morfologia é o estudo da estrutura das palavras. Em biologia, morfologia esta relacionada mais diretamente a forma de um organismo. A forma de uma folha pode ser usada para identificar uma planta ou a forma de uma colônia de bactérias pode ser usada para identificar sua variedade.

Morfologia digital é um caminho para descrever ou analisar a forma de um objeto digital.

A morfologia digital é uma ciência relativamente recente, pois só os computadores digitais permitiram seu uso na pratica. Por outro lado os matemáticos a consideram uso da teoria de conjuntos que é uma área bem estudada.

A idéia de morfologia digital é que uma imagem consiste de um conjunto de "picture elements" (pixels) que são reunidos em grupos tendo uma estrutura bidimensional (forma).

Certas operações matemáticas em conjuntos de pixels podem ser usadas para ressaltar aspectos específicos das formas permitindo que sejam contadas ou reconhecidas.

As operações básicas da morfologia digital são a erosão, em que pixels que não atendem a um dado padrão são apagados da imagem, e dilatação, em que uma pequena área relacionada a um pixel é alterada para um dado padrão. Todavia, dependendo do tipo de imagem sendo processada (preto e banco, tons de cinza ou colorida) a definição destas operações muda, assim cada tipo deve ser considerado separadamente.

OPERAÇÕES BINARIAS

Operações morfológicas binarias são definidas em imagens com pixels pretos e brancos somente. Um objeto é considerado ser um conjunto matemático de pixels pretos, cada pixel é identificado pelos seus índices de linha e coluna sendo chamado de um ponto no espaço bidimensional (E² ). Ex. A= {(1,1),(3,3),(7,3)}.

DEFINIÇÕES BÁSICAS

Antes de conhecer as operações básicas da morfologia binaria precisamos rever algumas definições básicas com conjuntos matemáticos.

TRANSLAÇÃO

A translação do conjunto A pelo ponto x é definida, em notação de conjuntos, como:

• (A)_x = { c | c = a + x, a Î A}

REFLEXÃO

A reflexão do conjunto A é definida como:

 = { c | c = -a, a Î A} 

COMPLEMENTO

O complemento do conjunto A é o conjunto dos pixels não pertencentes ao conjunto A. Estes poderiam corresponder aos pixel brancos na figura ou na linguagem da teoria dos conjuntos:

A^c = {c | c Ï A} 

A interseção de dois conjuntos A e B é o conjunto de pixels pertencentes a ambos A e B:

A Ç B = { c | (( c Î A) Ù (c Î B))}

A união de dois conjuntos A e B é o conjunto de pixels que pertencem ou A ou B ou ambos:

• A È B = { c | ((c Î A) Ú (c Î B ))}

A diferença entre os conjuntos A e B é o conjunto de pixels que pertencem a A mas não pertencem a B:

A – B = { c | (c Î A) Ù (c Ï B)}

A dilatação do conjunto A pelo conjunto B é definida por:

• A Å B = { c | c = a + b , a Î A , b Î B }

EXEMPLO 1:

A = {(1,1),(1,2),(2,1),(2,2)}= 

B = {(0,0),(1,0)}= 

Para este caso a equação pode ser rescrita como:

A Å B = [A+ {(0,0)}] È [A + {(1,0)}]

A + {(0,0)} = {(1,1),(1,2),(2,1),(2,2)} =

(1,1) + (0,0) = (1,1)

(1,2) + (0,0) = (1,2)

(2,1) + (0,0) = (2,1)

(2,2) + (0,0) = (2,2)

A translação de qualquer pixel por (0,0) não altera sua posição.

A + {(1,0)} = {(2,1),(2,2),(3,1),(3,2)} =

(1,1) + (1,0) = (2,1)

(1,2) + (1,0) = (2,2)

(2,1) + (1,0) = (3,1)

(2,2) + (1,0) = (3,2)

A Å B = {(1,1),(1,2),(2,1),(2,2),(3,1),(3,2)} =
 
 
 
 

O pixel marcado com um "x" representa a origem (0,0) de cada imagem. A localização da origem é muito importante; No exemplo anterior se a origem do conjunto B fosse o pixel da direita, {(-1,0),(0,0)}, a dilatação acrescentaria pixels a esquerda na imagem A.

EXEMPLO 2:

A =  B = A Å B =
 
 
 
 

EXEMPLO 3:

A =  B = A Å B =
 
 

A={(1,1),(1,2),(2,1),(2,2)}

B={((-1,0),(0,-1),(0,1),(1,0)}

A Å B = [A+ {(-1,0)}] È [A+ {(0,-1)}] È [A+ {(0,1)}] È [A+ {(1,0)}]

A+ {(-1,0)} = {(0,1),(0,2),(1,1),(1,2)}

A+ {(0,-1)} = {(1,0),(1,1),(2,0),(2,1)}

A+ {(0,1)} = {(1,2),(1,3),(2,2),(2,3)}

A+ {(1,0)} = {(2,1),(2,2),(3,1),(3,2)}

A Å B = {(0,1),(0,2),(1,0),(1,1),(1,2),(1,3),(2,0),(2,1),(2,2),(2,3),(3,1),(3,2)}

EROSÃO BINARIA

A erosão da imagem A pelo elemento estrutural B pode ser definida como:

• A q B = { c | (B)_c Í A }

EXEMPLO 1:

A = {(1,1),(1,2),(2,1),(2,2)}= B = {(0,0),(1,0)}= 
 
 

O conjunto A q B é o conjunto de translações de B que alinham B sobre o conjunto de pixels pretos em A. Isso Significa que nem todas as translações necessitam ser consideradas, mas somente aquelas que inicialmente localizam sua origem de B em um membro de A. Existem 4 dessas translações:

B_(1,1) = {(1,1),(2,1)}

Como os pixels (1,1) e (2,1) são pretos na imagem A.

O pixel (1,1) no resultado será preto.

B_(1,2) = {(1,2),(2,2)}

Como os pixels (1,2) e (2,2) são pretos na imagem A.

O pixel (1,2) no resultado será preto.

B_(2,1) = {(2,1),(3,1)}

Como o pixel (3,1) não é pretos na imagem A.

O pixel (2,1) no resultado não será preto.

B_(4,4) = {(4,4),(5,4)}

Como o pixel (5,4) não é pretos na imagem A.

O pixel (4,4) no resultado não será preto.

A q B = { (1,1) | B_(1,1) Í A} È { (1,2) | B_(1,2) Í A}

EXEMPLO 2:

A =  B = A q B =

A={(1,1),(3,3),(3,4),(4,3),(4,4)}

B={(0,0),(0,1),(1,0),(1,1)}

B_(1,1) = {(1,1),(1,2),(2,1),(2,2)}

B_(3,3) = {(3,3),(3,4),(4,3),(4,4)}

B_(3,4) = {(3,4),(3,5),(4,4),(4,5)}

B_(4,3) = {(4,3),(4,4),(5,3),(5,4)}

B_(4,4) = {(4,4),(4,5),(5,4),(5,5)}

A q B = { (3,3) | B_(3,3) Í A} 

EXEMPLO 3:

A =  B = A q B =

A={(3,3),(3,4),(4,3),(4,4)}

B={(-1,0),(0,-1),(0,1),(1,0)}

B_(3,3) = {(2,3),(3,2),(3,4),(4,3)}

B_(3,4) = {(2,4),(3,3),(3,5),(4,4)}

B_(4,3) = {(3,3),(4,2),(4,4),(5,3)}

B_(4,4) = {(3,4),(4,3),(4,5),(5,4)}

A q B = Æ

A erosão não é o inverso da dilatação, somente em alguns casos de erosão isso ocorre. Erosão e dilatação são duais no seguinte sentido:

• ( A q E )^c = A^cÅ Ê

ABERTURA

A aplicação de uma erosão imediatamente seguida por uma dilatação usando o mesmo elemento estrutural é referida como uma operação de abertura "opening". O nome abertura descreve o efeito dessa operação que tende a abrir pequenos vazios ou espaços entre objetos próximos numa imagem. Este efeito é mais facilmente observado quando são usados elementos estruturais simples.

• A ° B = (A q B) Å B

EXEMPLO:

A = B = A q B = (A q B) Å B =

 FECHAMENTO

Um Fechamento "Closing" é similar a uma abertura exceto que a dilatação é realizada primeiro seguida pela erosão usando o mesmo elemento estrutural. Se uma abertura cria pequenos vazios na imagem, um Fechamento irá preencher ou fechar os vazios. A operação fechamento pode remover muitos dos pixels brancos de ruído.

A · B = (A Å B) q B

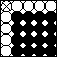A =  B = A Å B = (A Å B) q B =
 
 

MORFOLOGIA DE TONS DE CINZA

O uso de tons de cinza introduz uma enorme complicação tanto no conceito como na implementação. Um pixel pode agora ter qualquer valor inteiro, assim a facilidade de considerar a imagem como um conjunto desaparece.

DILATAÇÃO DE TONS DE CINZA

A dilatação em imagens de tons de cinza pode ser calculada como:

• (A Å B) = max {A(i – x , j – y) + B(x , y) | (i – x , j – y) Î A , (x, y) Î B}

1. Posiciona-se a origem do elemento estrutural sobre o primeiro pixel da imagem a ser dilatada. 
2. Calcula-se a soma de cada par correspondente de valores de pixels do elemento estrutural e da imagem. 
3. Acha-se o valor máximo de todas essas somas, e armazena-se o pixel correspondente na imagem de saída para este valor. 
4. Repete-se este processo para cada pixel da imagem a ser dilatada.

1. Valores negativos podem ser alterados para zero (underflow). 
2. A imagem inteira poderia ter seus valores aumentados para que o menor valor de pixel fosse zero mantendo os valores relativos entre os pixels.

A Erosão em imagens de tons de cinza pode ser calculada como:

• (A q B) = min {A(i – x , j – y) – B(x , y) | (i – x , j – y) Î A , (x, y) Î B}

1. Posiciona-se a origem do elemento estrutural sobre o primeiro pixel da imagem que sofre erosão. 
2. Calcula-se a diferença de cada par correspondente de valores de pixels do elemento estrutural e da imagem. 
3. Acha-se o valor mínimo de todas essas diferenças, e armazena-se o pixel correspondente na imagem de saída para este valor. 
4. Repete-se este processo para cada pixel da imagem que sofre erosão.

ABERTURA TONS DE CINZA

O processo de abertura funciona da mesma forma que definido anteriormente só que usa dilatação e erosão de tons de cinza. Isto é, a abertura usa uma erosão de tons de cinza seguida de uma dilatação de tons de cinza usando o mesmo elemento estrutural.

FECHAMENTO TONS DE CINZA

O processo de fechamento funciona da mesma forma que definido anteriormente só que usa dilatação e erosão de tons de cinza. Isto é, o fechamento usa uma dilatação de tons de cinza seguida de uma erosão de tons de cinza usando o mesmo elemento estrutural.

REFERÊNCIAS BIBLIOGRÁFICAS

GOMES, Jonas & VELHO, Luiz. Computação Gráfica: Imagem. Rio de Janeiro, IMPA/SBM, 1994.

GONZALEZ, Rafael C. & WOODS, Richard E.. Digital Image Processing. Reading, Addison-Wesley ,1992.

PARKER, J. R.. Algorithms for Image Processing and Computer Vision. New York, John wiley & Sons, 1997.

RUSS, John C. . The image processing handbook. 2 ed., Boca Raton, CRC Press, 1995.
 

Contato:

Tel.: +55-48-331 7552/9498
FAX: +55-48-331-9770
awangenh@inf.ufsc.br