Visualização Realística em 3D, zbuffering e Raytracing

ine 5341
Programa

OpenGL

Links

Bibliografia

Plano de Ensino

Trabalhos de
Alunos de
Semestres
Passados

Parte II - Computação Gráfica Avançada
Visualização Realística em 3D, zBuffering e Raytracing

2.3. Buffer de Profundidade - z-Buffering

2.4. Conversão de Varredura (Scan Conversion)

2.5. Modelando a Iluminação de um Objeto

2.7. Tutorial de Raytracing usando POV-Ray

2.8. O Método da Radiosidade: Modelando Radiância e Interação Luminosa entre Objetos

2.9. Material Fotográfico para o Trabalho de Modelagem em POV-Ray

Conversão por Varredura (Scan Conversion)

Este material se baseia em parte nas On-Line Computer Graphics Notes, Computer Graphics Group, Computer Sciences Department, University of California, Davis, originalmente escritas por Ken Joy.

No começo deste texto falamos na justificativa do porquê de não tratarmos algoritmos para desenho de linhas e polígonos no início deste curso de Computação Gráfica: porque hoje em dia não precisamos implementar estes algoritmos para fazer o que desejamos quando estamos trabalhando com um sistema básico de CG, como no caso de nosso sistema desenvolvido na primeira parte deste texto. Para a nossa projeção 3D de modelos de arame, nos bastavam os algoritmos de desenho de linhas que hoje em dia vêm embutidos em qualquer linguagem de programação, sem que tivéssemos que nos preocupar como foram implementados ou o que é que de fato estavam fazendo. Essa nossa relação de armistício com a programação em baixo nível em CG terminou: para uma implementação adequada de algoritmos de raytracing é necessário que se faça o passo de desenhar explícitamente um polígono pixel a pixel e de se determinar onde um determinado polígono em coordenadas de mundo vai gerar um pixel e onde não o fará. Para tanto vamos utilizar os algoritmos clássicos de conversão por varredura.

Uma operação fundamental extensivamente utilizada para visualização em CG é o proceso de conversão por varredura ou rasterização (scan conversion ou rasterization). Dado um polígono em espaço de imagem (de mundo), este processo determina os pixels que interceptam este polígono.

A Conversão por Varredura é um procedimento que é largamente utilizado em Computação Gráfica. É um procedimento bastante simples, organizado em torno de um paradigma de rastreamento de bordas, que pode ser implementado através de um algoritmo que utiliza a simples adição de incrementos sobre valores-base previamente calculados. Este método é utilizado em algoritmos de superfícies visíveis (visible-surface algorithms), técnicas de sombreamento incremental (incremental-shading techniques), algoritmos de preenchimento de polígonos, algoritmos de aceleração de raytracing e outras tarefas similares.

Um dos usos primários do método é a determinação de valores de profundidade z para os polígonos na cena, o que nos permite reter somente polígonos visíveis para renderização ao final de nossos cálculos, através da utilização posterior de um algoritmo de Buffer de Profundidade sobre os dados de coordenada z obtidos. Podemos, no entanto, também utilizar quantidades relacionadas a grandezas como cor, textura e outros parâmetros nos nossos nodos de pontos terminais e incrementar esses fatores também, incluindo esses valores no algoritmo de forma similar ao que será feito com a cálculo da coodenada z.

Este capítulo é organizado nas seguintes seções:

1. Conversão por Varredura de Trapézios em Espaço de Dispositivo
2. Realizando a Varredura
3. Inicializando o Rastreador de Bordas
4. Atualizando o Rastreador de Bordas para Linhas de Varredura Subseqüentes
5. A Estrutura de Dados de Pontos Finais
6. Identificando os Pixels Interceptados a cada Linha de Rastreamento
7. Incrementando o valor de Z para Pixels Consecutivos
8. Estabelecendo um Valor de Profundidade para Cada Pixel
9. Toques para Quem quer ir mais Fundo

Conversão por Varredura de Trapézios em Espaço de Dispositivo

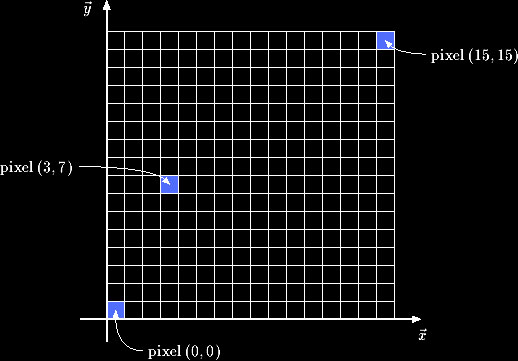
A conversão de varredura é o processo de se encontrar os pixels de tela que interceptam um polígono. Para realizar isto, normalmente criamos uma cópia dos dados do espaço de imagem (coordenadas do mundo) escalonada para corresponder aproximadamente à resolução da nossa viewport. Este espaço, comumente chamado de espaço de dispositivo, é parametrizado de tal forma que o canto inferior esquerdo está em (0,0), de forma que todos os pixels podem ser indexados por inteiros.

$\includegraphics {figures/device-space}$

Para a conversão por varredura de um polígono neste espaço, nós vamos dividir o polígono em uma série de trapézios, como mostrado na figura abaixo, e então converter por varredura cada um destes trapézios. Cada trapézio será gerado de forma que que as boirdas superior e inferior do trapézio sejam paralelas às linhas de varredura, possuindo y constante nesta região. Também levamos em conta trapézios degenerados sob a forma de triângulos, que possuem o topo ou a base com comprimento zero. Na figura abaixo, os trapézios superior e inferior do desenho são de fato triângulos.

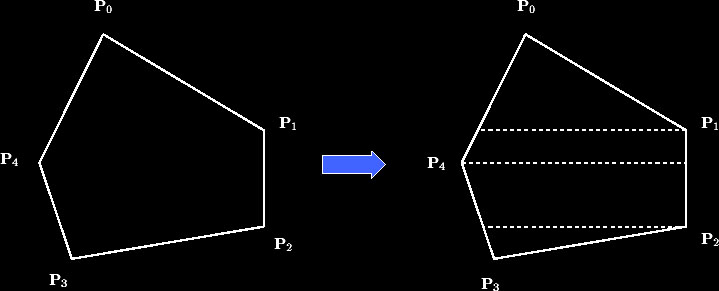
$\includegraphics {figures/trapezoids-from-polygons}$

A união de todos os pixels que interceptam o conjunto de trapézios será o conjunto de pixels que intercepta o polígono.

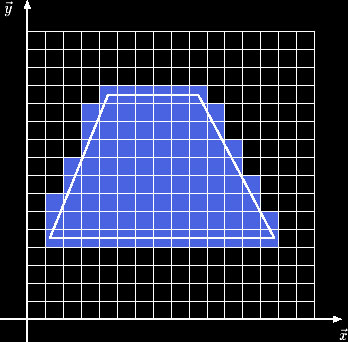
$\includegraphics {figures/pixels-covering-a-trapezoid}$

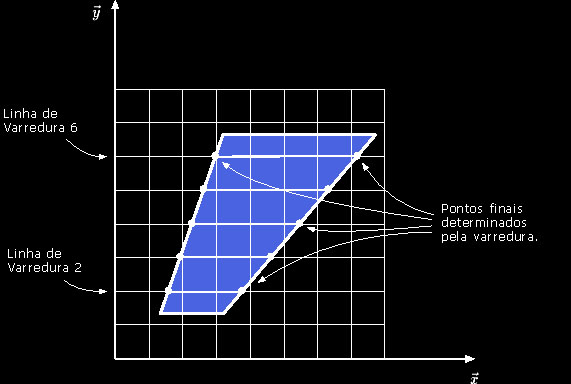
Realizando a Varredura

A idéia aqui é simples. Vamos criar um rastreador de bordas que segue os pontos finais das linhas formadas pela intersecção de cada linha de varredura com o trapézio.

$\includegraphics {figures/edge-tracker-1}$

Este rastreador de bordas pode ser definido com facilidade como uma estrutura de dados simples que é inicializada para a linha de varredura no topo de cada trapézio e atualizada para cada linha de varredura subseqüente.

Inicializando o Rastreador de Bordas

Suponha que seja dada uma borda definida pelos pontos P₁ = (x₁, y₁, z₁ ) e P₂ = (x₂, y₂, z₂ ), definida em espaço de dispositivo. Se definirmos Dx = x₂ - x₁, eDy = y₂ - y₁, então a figura abaixo mostra como calcular o ponto inicial (somente os valores de x e y são mostrados por questão de simplicidade).

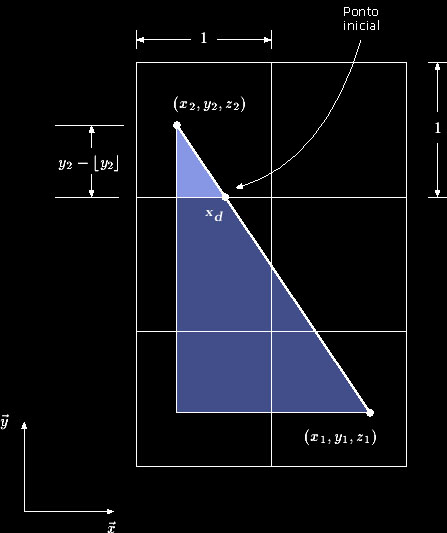
$\includegraphics {figures/edge-tracker-2}$

Podemos ver que o ponto inicial é dado por:

( x₂ + x_d, , z₂ + z_d)

onde é o valor discretizado de y₂, na posição da linha de varredura-base mais próxima abaixo de y₂, ou seja, valor inteiro da linha de pixels onde o valor y₂ cairá dentro. Para calcular x_d, observamos que há dois triângulos similares na ilustração e que podemos escrever:

$\displaystyle \frac{x_d}{y_2-{\lfloor} y_2 {\rfloor}} = \frac{x1 - x2}{y2 - y1}= -\frac{dx}{dy}$ ou $\displaystyle x_d = - ( y_2-{\lfloor} y_2 {\rfloor} ) \frac{\Delta x}{\Delta y}$ De forma análoga, podemos calcular: $\displaystyle z_d = - ( y_2-{\lfloor} y_2 {\rfloor} ) \frac{\Delta z}{\Delta y}$

Atualizando o Rastreador de Bordas para Linhas de Varredura Subseqüentes

Suponha que seja dada uma borda definida por dois pontos P₁ = (x₁, y₁, z₁ ) e P₂ = (x₂, y₂, z₂ ), definidos em espaço de dispositivo. Se definirmos Dx = x₂ - x₁, Dy= y₂ - y₁, e Dz = z₂ - z₁,então a figura abaixo mostra como atualizar o rastreador de bordas. Por razões de simplicidade omitimos a coordenada z.

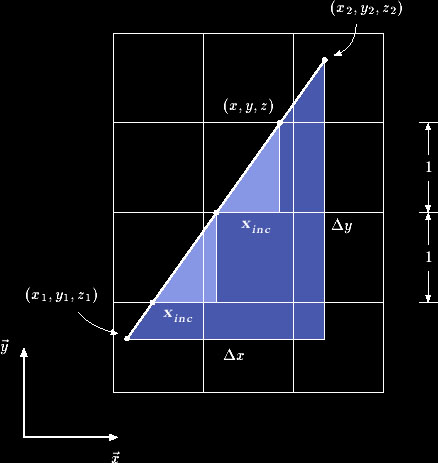
$\includegraphics {figures/edge-tracker-3}$

Aqui novamente temos triângulos similares e pode-se facilmente ver que para mover o rastreador de uma linha de varredura para a outra somente necessitamos de atualizar seu ponto final:

(x, y, z)

para $\displaystyle (x - x_{inc}, y - 1, z - z_{inc})$ e este mesmo cálculo funciona para qualquer ponto final. Podemos calcular x_inc diretamente a partir dos triângulos similares: $\displaystyle x_{inc} = \frac{\Delta x}{\Delta y}$ e similarmente $\displaystyle z_{inc} = \frac{\Delta z}{\Delta y}$ Desta forma, a atualização dos pontos finais do rastreador é muito simples; tudo o que temos de fazer é adicionar incrementos simples às coordenadas x, y e z , e movemo-nos para o ponto final da próxima linha.

A Estrutura de Dados de Pontos Finais

A forma mais simples de se implementar um rastreados de bordas de trapézios é criar-se uma estrutura de dados simples que contenha tanto a informação (x, y, z) dos pontos finais como dos incrementos que são necessários para ir do ponto final de uma linha de varredura à outra. Um nodo desta estrutura contém pelo menos a seguinte informação:

$\begin{singlespace}\small\begin{center}\begin{tabular}{ \vert c \vert }\hline......\ [-.5em]$y_{min}$\ \\ [.5em]\hline\end{tabular}\end{center}\end{singlespace}$

onde(x,y,z) é o ponto final, x_inc é o incremento adicionado à coordenada x para ir de uma linha de varredura à outra, z_inc é o incremento adicionado à coordenada z para ir de uma linha de varredura à outra e y_min é o limite inferior do trapézio que indica ao algoritmo quando parar de rastrear.

Identificando os Pixels Interceptados a cada Linha de Rastreamento

Para encontrar os pixels que interceptam um trapézio, criamos dois rastreadores de bordas e percorremos o trapézio no sentido y, linha de varredura por linha de varredura. Isto nos permite determinar, para cada linha de varredura, quais são os pontos finais de um segmento de reta que forma a intersecção da linha de varredura com as bordas laterais do trapézio.

Para encontrar quais são so pixels que interceptam o trapézio em uma determinada linha de varredura, nós precisamos apenas determinar as coordenadas do canto esquerdo inferior de cada pixel. Se os pontos finais( x_esq,y , z_esq) e ( x_dir,y , z_dir) calculados na linha de varredura em y, então os pixels que interceptam o trapézio são indexados por:

$\displaystyle ({\lfloor} x_{right} {\rfloor},y)$

$\includegraphics {figures/edge-tracker-4}$

Incrementando o valor de Z para Pixels Consecutivos

Estabelecer um incremento para o valor de z à medida que avançamos de uma linha de varredura para outra é bastante simples. A mesma coisa vale quando nos movemos de um pixel a outro, embora os dois incrementos sejam diferentes. Ambos os incrementos podem ser calculados diretamente a partir do vetor normal do trapézio, se assumirmos que o trapézio seja planar, como se assume para todo polígono que é tratado com as regras da geometria plana.

Oberve aqui, que o único polígono que tem necessariamente que ser planar é um triângulo, onde os seus três vértices por definição descrevem um plano. Polígonos com numero de vértices maior do que 3 não precisam necessariamente possuir todos os seus vértices contidos em um único plano. Um polígono não planar é possível de ser definido, mas ele não serve para este algoritmo e deve ser sempre obrigatoriamente dividido em subpolígonos planares, normalmente triângulos. Esta divisão sempre é possível e este teste é implementado em alguuns lugares como parte do sistema. Browsers de VRML, por exemplo, sempre realizam o teste de planaridade com algum polígono dado como superfície fechada e dividem-no em triângulos caso não seja planar, antes de renderizá-lo.

Para vermos como isto funciona, seja ${\vec n}$ o vetor normal ao trapézio que é definido em espaço de dispositivo. Se nós possuímos dois pontos Q₁ e Q₂ no espaço de plano do trapézio, então sabemos que $\displaystyle {\vec n} \cdot ( {\bf Q} _2 - {\bf Q} _1 ) = 0$ ^. (Q₂ - Q₁) = 0, uma vez que Q₂ - Q₁ é obrigatoriamente um vetor neste plano e o produto escalar de vetores perpendiculares, o que estes obrigatoriamente serão, é sempre nulo. Agora suponha que façamos Q₁ = (x, y, z) e Q₂ = (x + 1, y, z + z_hinc) o que representa as coordenadas de dois pixels consecutivos em espaço de dispositivo e onde z_hinc é desconhecido.

Se fizermos ${\vec n} = <x_n, y_n, z_n>$ = < x_n, y_n, z_n >, poderemos calcular o produto escalar como

$\displaystyle = <x_n, y_n, z_n> \cdot ( (x+1, y, z+z_{hinc}) - (x,y,z) )$

equação que pode ser resolvida para dar

$\displaystyle z_{hinc} = -\frac{x_n}{z_n}$

que é o incremento horizontal de z pixel a pixel. Observe que este não é o memso que o incremento vertical de z.

Estabelecendo um Valor de Profundidade para Cada Pixel

Já que um pixel é identificado por usa coordenada de espaço de dispositivo no canto inferior esquerdo do pixel, é útil para nossos algoritmos de renderização serem capazes de atribuir um valor z para um trapézio neste ponto. Nós já demonstramos como calcular os valores de z nos pontos finais. Nós somente necessitamos modificar este valor de forma que seja apropriado para a coorenada do valor inferior esquerdo de um pixel. Portanto, dado um ponto extremo (x, y, z), considere a figura abaixo:

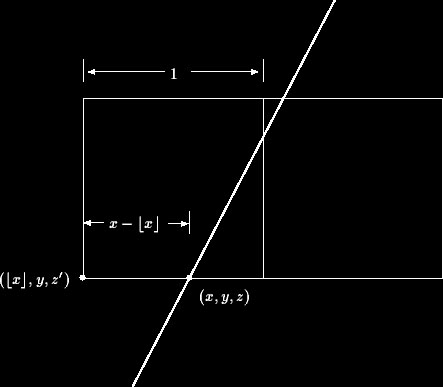
$\includegraphics {figures/edge-tracker-5}$

Olhando a figura, podemos ver que deveríamos subtrair de z uma porção do incremento horizontal de zque corresponde à distância de x do lado esquerdo do pixel. Podemos expressar isto da seguinte forma:

$\displaystyle z' = z - (x - {\lfloor} x {\rfloor}) z_{hinc}$

com este valor de z e o incremento horizontal de z , z_hinc podemos especificar um aprofundidade para cada pixel do trapézio ao longo da linha de varredura.

Usando os cálculos acima, podemos utilizar a estrutura de dados de pontos finais para organizar mecanismos de rastreamento de bordas. Esta informação, uma vez que os trapézios serão sempre planos, pode então ser utilizada de forma linear para atribuir um valor de z local para todos os pixels, mesmo internos, do trapézio.

Toques para Quem quer ir mais Fundo

A abordagem que nós demos ao tema neste capítulo é extremamente superficial e simples. O objetivo deste capítulo é que você entenda os princípios gerais do processo e saiba o que um Raytracer ou OpenGL faz. Se você implementar o método como está descrito aqui, ele vai funcionar, mas os seus resultados práticos não vão se comparar a implementações avançadas, como as encontradas em Raytracers como POV-Ray ou RADIANCE. Se você deseja aprofundar o assunto de conversão por varredura, sugerimos o site a UC Davis. Este site é, na Internet, de longe, a melhor fonte de informação séria e confiável. Vá para a página das On-Line Computer Graphics Notes, mantidas por professores e estudants do Computer Graphics Group, Computer Science Department, na UC Davis.

2.1. O que é Raytracing ?