
Visão Computacional
1. Representação de
imagens
2. Filtragem de imagens
3. Detecção de Bordas
4. Segmentação Simples
5. Crescimento de Regiões
6. Segmentação com
Filtros
7. Segmentação a Cores
8. Análise de Texturas
9. Análise de Texturas
Multiescalar
10. Redes Neurais
11. Morfologia Matemática
12. Convolução
13. Esqueletonização
14. Técnicas Estatísticas
15. Fractais
16. Reconhecimento de
Formas
17. Representação de
Objetos
18. Quadtrees e Octrees
19. Visão Estereo
20. Inteligência Artificial
21. Controle de qualidade
22. Robótica
23. Medicina
24. Sensoriamento remoto
Prof. Aldo von Wangenheim
Currículo...
Publicações
Pesquisa
Projetos
Ensino de Graduação
Ensino de Pós Graduação
Cursos
Aluno: Alex Sandro Moretti
Medição de Bobina de Papel Utilizando Visão Computacional
Disciplina Visão Computacional
Prof. Dr. Aldo WangenheimIntrodução
Com as técnicas de visão computacional foi implementado uma possível solução na medição da largura de bobinas de papel em uma industria. Nesta industria precisa-se medir a largura da bobina e seu peso, onde o peso é feito por uma balança eletrônica e a largura feito por um operário pelo processo manual, ambas a informações devem ser passados para o computador, onde o peso é passado via serial e a largura por digitação. Para viabilizar mais o processo na empresa há necessidade em contornar este processo manual, e neste artigo esta descrito um protótipo que possa suprir tal necessidade.
Definição do problema
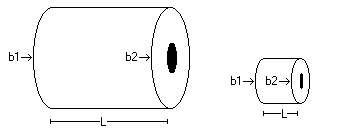
Por um certo tipo de controle da empresa há somente necessidade de medir a largura da bobina. As dimensão da bobina estão descrita na figura abaixo, onde L (largura) varia entre 50cm a 3 metros. E como a bobina de papel é branca fica muito mais fácil em trabalhar com a análise de imagem, pois não precisaremos trabalhar com texturas.
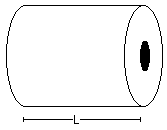
Bobina de PapelO processo é o seguinte, o operário pela empilhadeira pega a bobina do depósito e leva até a balança eletrônica deixando-a encima da mesma. A balança pesa a bobina e passa para o computador o seu peso, e logo depois o operário mede a espessura da bobina por uma trena e digita-a no computador.
Com isto há uma deficiência no perfumasse do processo, onde a empresa ver a necessidade em automatizar o processo de medição.
Medição de largura da bobina
Para fazer a medição da largura da bobina necessitaremos fotografar e digitalizar a foto, com a imagem digitalizada trabalharemos em calcular a largura da bobina, isto consiste em localizar as bordas da bobina (b1 e b2) e calcular as distancias entre elas. Mas o processo não é tão simples assim, pois existem certos fatores que devem ser levados em consideração que influenciam nos cálculos.
Acompanhe com a figura abaixo. Antes de mencionar os fatores é preciso definir alguns parâmetros da bobina e da câmera. Parâmetros da bobina são: b1 é a borda lado esquerdo da bobina, b2 é a borda direita da bobina e L a largura da bobina. Parâmetros da câmera, é a objetiva com seus ângulos central e radiais, onde (a) é o angulo central, (b c) ângulos radiais laterais esquerdo e direito respectivamente e (d e) são os ângulos radiais verticais de cima e de baixo respectivamente.
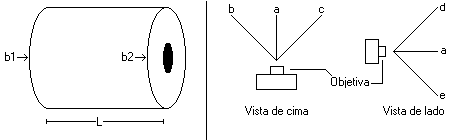
Parâmetros de bordas e da câmera digitalOs fatores que devem ser levados em considerações são:
1 - Detectar borda
Devemos abstrair da foto somente as bordas dos objetos e desprezando as demais informações, isto será explicado logo depois em pré processamento de imagens.
2 – A distância entre b1 e b2
O angulo de inclinação do objeto em relação a objetiva da câmera influencia na distancia entre b1 e b2. Se um objeto colocado perpendicularmente com a objetiva da câmera teremos um distancia de b1 e b2 = X. E se o mesmo objeto estiver na mesma distancia da câmera com uma inclinação em relação a objetiva da câmera a distancia entre b1 e b2 será menor a X.
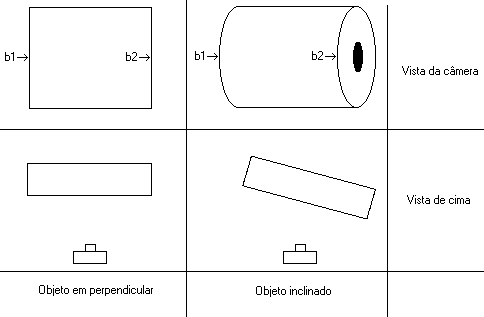
Objeto perpendicular e Objeto InclinadoMas não basta colocarmos o objeto em perpendicular a câmera, mas sim em perpendicular a angulo central da objetiva da mesma. Como somente se precisa calcular a largura da bobina, vamos só levar em consideração os ângulos radiais laterais e desprezando os demais ângulos. Por que levar em conta os ângulos radiais laterais, porque se o objeto se encontra mais a esquerda do angulo central da objetiva, o objeto esta inclinado no sentido horária em relação a objetiva. E se o objeto se encontra mais a direita do angulo central da objetiva, o objeto esta inclinado no sentido anti-horárioem relação a objetiva.
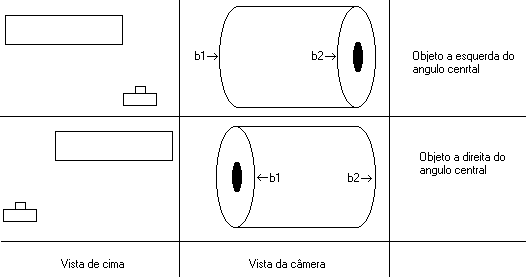
Objeto a esquerda e a direita do angulo central da objetiva3 – Distancia entre o objeto e a câmera
Se um objeto de 1 metro de largura estiver a 2 metros da câmera terá uma distancia entre b1 e b2 igual a X. E se o mesmo objeto estiver a 10 metros da câmera a distancia entre b1 e b2 será bem menor que X. ou seja, pela propriedade cônica da visão, o objeto se torna cada vez menor na medida que o mesmo se afasta de nossa visão diminuindo o angulo de visão.
Distancia a 2 metros Distancia a 10 metros
Todos esses fatores influenciam nos cálculos da largura da bobina. Como vamos soluciona-los? A idéia é obtermos um certa referencia para comparação, como fazer isso? Vamos projetar na superfície da bobina via lazer um circulo para tomarmos referencias, por que um circulo, pois dependendo do tamanho do circulo visto na foto poderemos calcular a distancia do objeto em relação a câmera, e dependendo da deformação do circulo, formando ou não uma elipse, calcularemos a inclinação do objeto em relação da câmera. Se na foto aparecer um circulo perfeito, quer dizer que a bobina não esta inclinada e se aparecer uma elipse o objeto está inclinado em relação a inclinação da mesma

Objeto inclinado Horário Objeto não Inclinado Objeto Inclinado Anti Horário
Objeto perto da câmera

Objeto inclinado Horário Objeto não Inclinado Objeto Inclinado Anti Horário
Objeto longe da câmera
Então para calcularmos a distancia entre as bordas b1 e b2 devemos suprir três variáveis:
Estes fatores foram levantados em conta, pois o operador da empilhadeira vai colocar a bobina sobre a balança de qualquer jeito, longe ou perto, inclinado ou não em relação a câmera. Lógico que especificaremos ao operário a coloca a bobina dentro de um certo limite aceitável para medição.
- A distancia do objeto em relação a câmera
- A inclinação do objeto em relação a câmera
- A distancia do objeto em relação ao angulo central da objetiva da câmera
Para podermos calcular a largura da bobina devemos seguir certos procedimentos, tais como:
Definição da Câmera, iluminação e Posicionamento
- Definir câmera, lazer e iluminação
- Posicionar câmera e o lazer
- Fotografar objeto
- Fazer pré processamento da imagem
- Efetuar cálculos referentes as variáveis mencionadas acima
A câmera utilizada para o protótipo foi uma WebCam colorida com resolução de 352 x 288 pixels por 24 bits color com conexão USB.
O lazer utilizado foi do tipo apresentação com projeção de um circulo sob o objeto. O angulo de abertura da projeção do circulo tem que ser diferente do que angulo de visão da objetiva, pois se for o mesmo angulo, a projeção terá o mesmo tamanho na foto tanto se o objeto estiver longe como perto da câmera.
O lazer esta fixo logo atrás e acima da câmera onde seu ponto de incidência do lazer coincide com alinhamento da objetiva.
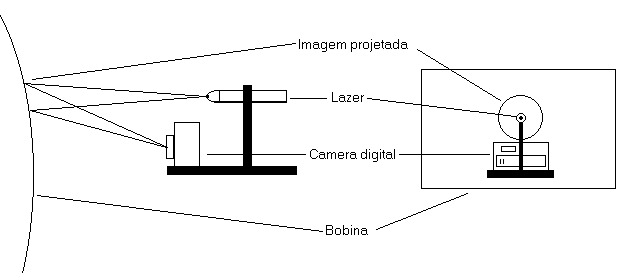
Posicionamento da câmera e lazerO local deverá conter iluminação suficiente para podermos detectar as bordas no processamento de imagem, e também para obtermos uma boa qualidade da digitalização da imagem.
Digitalização da Imagem
Após colocado a bobina na balança, a balança espera para o peso se estabilizar, e quando peso se estabiliza ele é transmitido ao computador, quando o peso é recebido será acionado a câmera para obter a foto do objeto, e começa todo processamento de imagem para calcular a largura da bobina.
Pré Processamento da Imagem
Os pré processamentos de imagem que melhor obteve resultado para este protótipo estão dividido em:
Para podermos trabalhar com imagem via computacional, trabalharemos com duas matrizes bidimensionais de mesmo tamanho em resolução da imagem, ou seja, uma matriz de 352 x 288, cada posição da célula na matriz corresponde a posição na imagem e cada valor da célula corresponde a o valor do pixel. A matriz que vai armazenar a imagem será chamada de IMAGEM, e a outra matriz que vai auxiliar nos processamentos da imagem será chamado de IMAGEM_T.
- Imagem Monocromática
- Smooth
- Detetor de bordas
- Threshold
- Erosion
Imagem Monocromática
Neste projeto o tratamento de cores foi abordado com 16 bits de cor, ou seja, temos uma variação de cores RGB de 0 a 65535 para o pixel, mas existem placas de vídeo que trabalham com 8, 16, 24 e 32 bits de cor.
Para uma rápida, eficiente pré processamento de imagem, uma imagem monocromática é a ideal. Mas para podermos passar a imagem colorida para monocromática teremos que entender um pouco sobre bits de cor RGB da placa de vídeo do computador, não vamos entrar em detalhes sobre posição de pixel na memória RAM da placa de vídeo e nem sobre os processos de sincronismo verticais e horizontais do monitor e da placa, pois estes o sistema operacional se encarrega em executar, o que nos interessa são as coordenadas dos pixels e seus valores. Então vamos nos concentrar somente nos valores de cada pixel na representação de 16 bits na placa.
Os 16 bits da cor está divididos em três partes, os 5 primeiros bits mais significativos estão representado para o vermelho (R), os 6 bits do meio representa o verde (G) e os últimos 5 bits menos significativos representam o azul (B).
Representação dos bits de cor para 16 bits
Deduzimos então que:
Trabalhando somente com as tonalidades em azul.
Trabalhando somente com as tonalidades em verde.
- Valores de 0 a 31
Trabalhando somente com as tonalidades em vermelho.
- Valores de 32 a 2016 incrementando de 32
- Valores de 2048 a 63488 incrementando de 2048
Neste processo de passagem de uma imagem colorida para tons de cinzas, foi pego os 5 bits do R, os cinco bits mais significativos do G, desprezando o primeiro bit do G que é o bit 5, os cinco bits do azul, somados e dividido por três, obtendo a normalização das três cores RGB que é o monocromático, e depois repassado para cada bits correspondente a RGB o valor da normalização.M = (R+G+B) / 3
R = M
G = M
B = M
Preste atenção, para este processos os bits correspondente a cada RGB, foram partidos em três, e cada uma parte foram considerados na formula como potência começando do zero, e não da potência correspondente da posição que se encontra no valor original. Exemplo
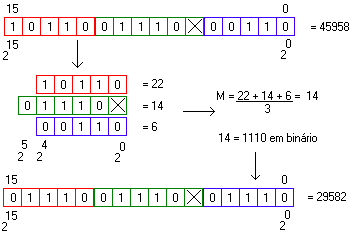
Neste procedimento obtivermos somente 31 níveis de cinza, mas esta é minha simples técnica, mas o padrão se encontra com 255 níveis de cinza, onde 0 é o preto e 255 é o branco, aqui 0 é preto e 31 branco.
Então atualizaremos a matriz IMAGEM com imagem vindo da câmera e aplicaremos a normalização em cada célula que corresponde a cada pixel.
Imagem colorida transformada para monocromática
Pseudo algoritmo
PARA TODA PIXEL DA FOTO FAÇA
PIXEL ATUAL MATRIZ IMAGEM = MEDIA RGB
SmoothSmooth quer dizer alisamento, é um pré processamento usado na imagem com o objetivo de suprir ruídos e pequenas flutuações na imagem. Infelizmente este método obscurece informações importantes sobre as bordas dos objetos, diminuindo um pouco da precisão da medição
O procedimento do alisamento consiste em cada pixel terá o valor a média de valores dos pixels vizinhos. Neste protótipo foi utilizado uma máscara de alisamento de 4 x 4, digo a máscara 4 x 4 quer dizer que a matriz IMAGEM é varrida cada 4 pixel coluna e 4 pixel linha a partir do pixel sendo atual, somando-as e depois divididas por seu lado ao quadrado, ou seja, a média. Exemplo com máscara 2 x 2:
Media Smooth com máscara 2x2

Aplicação do SmoothPseudo algoritmo
PARA TODOS OS PIXELD DA MATRIZ IMAGEM FAÇA
VARPIXEL = MEDIA DOS PIXELS VIZINHOS
MATRIZ IMAGEM = MATRIZ IMAGE_T PIXEL ATUAL DA MATRIZ IMAGEM_T = VARPIXEL
Detetor de bordas
Bordas em uma imagem são lugares com fortes intensidade de contraste, e neste fortes contrates freqüentemente se encontra os limites dos objetos, a descoberta de bordas de um objeto é muito utilizada em segmentação de imagem, onde a vantagem adicional é que a quantia de dados a serem analisados serão bem reduzidos, retendo a maioria das informações da imagem, e com essa redução há um custo baixo de processamento e de memória, consequentemente um aumento na eficiência de processamento.
As bordas corresponde a fortes iluminação que denominarão os gradientes, aonde os mesmos podem ser destacados calculados as derivadas da imagem.
Detectar bordas por processo por gradientes é a segunda técnica mais usada. Para calcularmos o gradiente o processo é dividido em duas máscaras, ou núcleos de convolução, uma para calcular o gradiente na direção x ,Gx, e outra mascara para calcular o gradiente na direção y, Gy. Gerando uma magnitude absoluta do gradiente. E em muitos implementação, a magnitude do gradiente é a única produção detetor de bordas, porém também poderíamos calcular a orientação da borda.
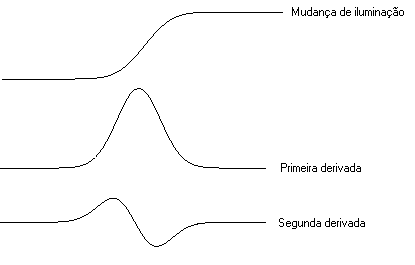
Derivadas da iluminação da imagem (Gradientes)
Existem vários operadores para detecção de bordas, tais como Kirsch, Laplace, Prewitt, Roberts, Robinson e outros afora, mas neste protótipo foi utilizado o operador Sobel por ser simples e obtém bons resultados que trabalha sobre orientação do gradiente. Mas o detetor que se monstra mais eficiente e complexo é o operador Canny.
Operador Sobel
O operador Sobel efetua em um espaço 2D a medida do gradiente em uma imagem e assim enfatiza as regiões que corresponde as bordas. Tipicamente isto é usado para encontrar a magnitude do gradiente absoluto para cada ponto em tons de cinza dentro da imagem.
Teoricamente, o operador consiste em um par de mascaras de 3×3 chamados de núcleos de convolução, como mostrado em Figura abaixo. Um núcleo é simplesmente ou outro mas girado em 90°.
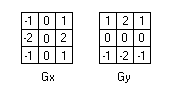
Núcleos de convoluçõesEstes núcleos são projetados para responder maximamente para bordas verticalmente e horizontalmente relativo a grade de pixel, um núcleo para cada uma das duas orientações (Gx e Gy). Os núcleos podem ser aplicados separadamente na imagem produzindo resultados separados e depois somados obtendo uma magnitude absoluta do gradiente. Podemos expressar a magnitude do gradiente pela formula:
Aproximando a fórmula acima pela a de baixo para simplificar a implementação e torna-lo mais rápido, mas no protótipo foi utilizado a fórmula de cima, mas deixarei a de baixo para facilitar a explicação .
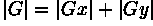
O ângulo de orientação da borda (relativo a grade de pixel) dando lugar ao gradiente de espaço é dada pela fórmula :
Neste caso, a orientação 0 quer dizer que a direção do contraste máximo do preto para o branco do sentido da esquerda para direita da imagem.
Freqüentemente, a única coisa quer o usuário vê é magnitude absoluta, que é o somatório dos dois componentes de gradientes (Gx e Gy). O somatório é feito pelo operador de pseudo-convolução mostrada abaixo.

Máscara pseudo convoluçãoUsando este núcleo a magnitude aproximada é dada por:
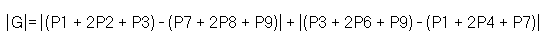
Neste protótipo somente foi usado os gradientes e não suas orientações.

Aplicação do operador SobelPseudo algoritmo
PARA CADA PIXEL DA MATRIZ IMAGEM FAÇA
VARPIXEL = G (magnitude do gradiente Gx e Gy)PIXEL ATUAL MATRIZ IMAGEM_T = VARPIXEL
MATRIZ IMAGEM = MATRIZ IMAGEM_T
ThresholdThreshold, especifica um valor limiar do pixel. Este processo é bem simples, consiste em fazer uma binarização da imagem, ou seja, vamos especificar um valor para o threshold entre 0 e 31, e percorremos a matriz IMAGEM, se o valor do pixel atual se encontra abaixo do threshold o valor desse pixel será substituído por 0 (preto), caso seja maior ou igual ao trheshold o valor será substituído por 31 (branco). Por isto que esse processo se chama binarização, pois após o processo do threshold a matriz IMAGEM somente contém dois valores o preto e o branco.

Aplicação do ThresholdPseudo algoritmo
THRESHOLD = 15
PARA CADA PIXEL DA MATRIZ IMAGEM FAÇA
SE PIXEL ATUAL DA MATRIZ IMAGEM < THRESHOLDPIXEL ATUAL MATRIZ IMAGEM = 0 (preto)SENAOPIXEL ATUAL MATRIZ IMAGEM = 31 (branco)
ErosionEste é classificado com morfologia de imagens, existem outras morfologias tais como: Dilation, Closing(Dilatação seguido de erosão), Opening(Erosão seguido de dilatação), Thiming, Skeletonization, Thickening ...
Como estamos trabalhando somente com imagem binária, a erosão consiste em retirar da imagem binária aqueles pixels diferente de 0 (preto) que não satisfazem as condições. Neste protótipo foi usado a seguinte mascara 3x3 abaixo:
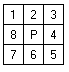
Máscara para erosãoEm cima dessa mascara a condição para erosão é o seguinte, se o pixel P da matriz IMAGEM que está sendo analisado existir alguns dos seus vizinhos (1,2,3,4,5,6,7 e 8) que seja 0(preto), então este pixel será passado para matriz IMAGEM_T como 0(preto), caso contrário será passado com 31(branco).

Aplicação da ErosãoPseudo algoritmo
PARA CADA PIXEL DA MATRIZ IMAGEM FAÇA
TODOS OS VIZINHOS DO PIXEL DA MATRIZ IMAGEM SÃO 31PIXEL ATUAL DA MATRIZ IMAGEM_T = 31SENAOPIXEL ATUAL DA MATRIZ IMAGEM_T = 0MATRIZ IMAGEM = MATRIZ IMEGEM_T
Efetuando Cálculo da largura da bobina
Para podermos calcular a largura da bobina, como mencionado anteriormente devemos resolver as seguintes variáveis.
Como a posição do lazer esta fixo junto à câmera o centro da elipse é sempre o mesmo, então sabemos onde se encontra o centro e por ele começaremos os cálculos.
- A distancia do objeto em relação a câmera
- A inclinação do objeto em relação a câmera
- A distancia do objeto em relação ao angulo central da objetiva da câmera
Primeiro variável é solucionada encontrando os eixos maiores e menores da elipse, e com eles determinaremos o tamanho da elipse e com conseqüência temos a relação da distancia da bobina em relação a câmera.
Segundo variável é solucionada pela detecção da inclinação dos eixos da elipse, que corresponde na inclinação da mesma. Sabendo a inclinação da elipse saberemos a inclinação da bobina, pois quem deformou a elipse foi a posição do objeto em relação a câmera.
Terceiro variável é solucionada encontrado as distancias entre as bordas laterias da bobina em relação ao centro da elipse, com isto determinaremos em que grau de inclinação se encontra a bobina em relação ao ângulo central da objetiva da câmera.
Com as três variáveis solucionadas podemos relacionar objetos com suas medidas e distancias, alimentando o algoritmo com essas relações deixamos apto para solucionar nova medições.
Conclusão
Neste procedimento não se obtém bons resultados para um boa precisão na medição, pois já na erosão junto com alisamento(smooth) já dificultamos a precisão. E como estamos trabalhando em medições em relação a pixels, a resolução da câmera não é satisfatória para obter uma boa precisão na medição. Então poderemos melhorar a precisão aumentando a resolução da câmera, também e melhorando a iluminação, colocando um controle automático de iluminação, pois neste experimento a intensidade do lazer saturou a câmera e houve um certo borrão que foi muito desconcertante no processamento de imagem onde dificulta a precisão também. Resumindo, este protótipo, não com muita precisão, mas consegue medir a largura da bobina .
Bibliografias
http://www.dai.ed.ac.uk/HIPR2/noise.htm
http://euclid.ii.metu.edu.tr/~ion528/demo/demochp.html
http://www.bmva.ac.uk/bmvc/1997/papers/055/node3.html
http://www.search.soton.ac.uk/cgi-bin/htsearch
http://my.netian.com/~avi97/kuim/hough.html
http://www.icaen.uiowa.edu/~dip/LECTURE/contents.html
http://www.eng.iastate.edu/ee528/sonkamaterial/chapter_2.htm
http://www.visc.vt.edu/armstrong/ee2984/sobel.html
http://yake.ecn.purdue.edu/~cetto/
http://203.162.7.85/unescocourse/computervision/61.htm#6.1
http://www.geog.buffalo.edu/~zy/hough_demo.htm
http://www.dai.ed.ac.uk/HIPR2/noise.htm
http://euclid.ii.metu.edu.tr/~ion528/demo/demo
http://www.ee.surrey.ac.uk/Research/VSSP/publications/1994.html
Anexos
#define draw_w 352
#define draw_h 288
unsigned int
ArrayGrey[255];
unsigned char
ImageIn[draw_w][draw_h],
ImageWork[draw_w][draw_h];
unsigned char
MaxColorGrey = 31,
Smooth = 1,
Threshold = 0;
//*************************************************************************************
//Create image grey
int FilterColor(char filter, char Area)
{
BITMAP
*image;
unsigned int
sl, sc, el, ec;
int
color, ret, x, y;
if (Area == Area1)
{
sl = range_draw1_sl; el = range_draw1_el;
sc = range_draw1_sc; ec = range_draw1_ec;
}
else
{
sl = range_draw2_sl; el = range_draw2_el;
sc = range_draw2_sc; ec = range_draw2_ec;
}
scare_mouse();
image = create_bitmap(draw_w, draw_h);
clear(image);
blit(screen, image, sc, sl, 0, 0, draw_w, draw_h);
for (x = 0; x <= draw_w; x++)
for(y = 0; y <= draw_h; y++)
{
color = getpixel(image, x, y);
putpixel(image, x, y, color_filter(filter, color));
}
blit(image, screen, 0 ,0 , sc, sl, draw_w, draw_h);
destroy_bitmap(image);
unscare_mouse();
return 0;
}
//**************************************************************************************
// CREATE ARRAY GRAY
int CreateArrayGrey(void)
{
unsigned int
color, point;
for (point = 0; point <= 255; point++)
ArrayGrey[point] = 0;
color = 0;
for (point = 0; point <= MaxColorGrey; point++)
{
ArrayGrey[point] = color;
color = color + 2113;
}
return 0;
}
//***********************************************************************************
// CREATE IMAGE monocromatic IN the array
int ImageCreate(char Area)
{
unsigned char
point;
unsigned int
pixel, lin,col, image_lin, image_col, sl, sc, el, ec;
FilterColor(filter_grey, Area);
col = 0; lin = 0;
for (image_lin = sl; image_lin < el; image_lin++)
{
for (image_col = sc; image_col < ec; image_col++)
{
//locate in ArrayGrey o yout point color
pixel = getpixel(screen, image_col, image_lin);
point = 0;
while ((ArrayGrey[point] != pixel) & (point <= 255))
point++;
if (Area == Area1)
ImageIn[col][lin] = point;
else
ImageWork[col][lin] = point;
col++;
}
col = 0;
lin++;
}
return 0;
}
//***************************************************************************************
// PLACE IMAGE OF THE MATRIX
int ImageDrawMatrix(unsigned char image[][draw_h])
{
int
pixel, col, lin, px_col, px_lin;
px_col = range_draw2_sc; px_lin = range_draw2_sl;
scare_mouse();
for (lin = 0; lin < draw_h; lin++)
{
for (col = 0; col < draw_w; col++)
{
putpixel(screen, px_col, px_lin, ArrayGrey[image[col][lin]]);
px_col++;
}
px_col = range_draw2_sc;
px_lin++;
}
unscare_mouse();
return 0;
}
//*************************************************************************************
// SMOOTH IMAGE
int ImageSmooth(void)
{
unsigned int
lin, col, top, botton, left, right, x, y, z, area;
ImageCreate(Area1);
//Clear Image Work
for (lin = 0; lin < draw_h; lin++)
for (col = 0; col < draw_w; col++)
ImageWork[col][lin] = 0;
for (lin = 0; lin < draw_h; lin++)
{
if (lin < Smooth)
top = 0;
else
top = lin - Smooth;
if (lin > draw_h - Smooth - 1)
botton = draw_h - 1;
else
botton = lin + Smooth;
for (col = 0; col < draw_w; col++)
{
if (col < Smooth)
left = 0;
else
left = col - Smooth;
if (col > draw_w - Smooth - 1)
right = draw_w - 1;
else
right = col + Smooth;
area = (right - left + 1) * (botton - top + 1);
z = 0;
for (x = left; x <= right; x++)
for (y = top; y <= botton; y++)
z = z + ImageIn[x][y];
ImageWork[col][lin] = z/area;
}
}
PlaceToImageIn();
return 0;
}
//********************************************************************************
//DILATION
int ImageDilation(void)
{
unsigned int
lin, col;
ImageCreate(Area1);
for (lin = 0; lin < draw_h; lin++)
for (col = 0; col < draw_w; col++)
ImageWork[col][lin] = 0;
// filter the image and store result in output array
for (lin = 1; lin < draw_h - 1; lin++)
for (col = 1; col < draw_w - 1; col++)
if (ImageIn[col][lin] == MaxColorGrey)
{
ImageWork[col - 1][lin - 1] = MaxColorGrey;
ImageWork[col - 1][lin ] = MaxColorGrey;
ImageWork[col - 1][lin + 1] = MaxColorGrey;
ImageWork[col ][lin - 1] = MaxColorGrey;
ImageWork[col ][lin ] = MaxColorGrey;
ImageWork[col ][lin + 1] = MaxColorGrey;
ImageWork[col + 1][lin - 1] = MaxColorGrey;
ImageWork[col + 1][lin ] = MaxColorGrey;
ImageWork[col + 1][lin + 1] = MaxColorGrey;
}
PlaceToImageIn();
return 0;
}
//**************************************************************************************
//Erosion
int ImageErosion(void)
{
unsigned int
x, lin, col;
ImageCreate(Area1);
for (lin = 0; lin < draw_h; lin++)
for (col = 0; col < draw_w; col++)
ImageWork[col][lin] = 0;
// filter the image and store result in output array
for (lin = 1; lin < draw_h - 1; lin++)
for (col = 1; col < draw_w - 1; col++)
if (ImageIn[col][lin] == MaxColorGrey)
{
if ( (ImageIn[col - 1][lin - 1] == MaxColorGrey) &&
(ImageIn[col - 1][lin ] == MaxColorGrey) &&
(ImageIn[col - 1][lin + 1] == MaxColorGrey) &&
(ImageIn[col ][lin - 1] == MaxColorGrey) &&
(ImageIn[col ][lin ] == MaxColorGrey) &&
(ImageIn[col ][lin + 1] == MaxColorGrey) &&
(ImageIn[col + 1][lin - 1] == MaxColorGrey) &&
(ImageIn[col + 1][lin ] == MaxColorGrey) &&
(ImageIn[col + 1][lin + 1] == MaxColorGrey) )
ImageWork[col][lin] = MaxColorGrey;
else
ImageWork[col][lin] = 0;
}
PlaceToImageIn();
return 0;
}
//**********************************************************************************
// SOBEL
int ImageSobel(void)
{
unsigned int
lin, col;
ImageCreate(Area1);
for (lin = 0; lin < draw_h; lin++)
for (col = 0; col < draw_w; col++)
ImageWork[col][lin] = 0;
// filter the image and store result in output array
for (lin = 1; lin < draw_h - 1; lin++)
for (col = 1; col < draw_w - 1; col++)
{
// Apply Sobel operator.
if (GradientY)
SobelY[col][lin] = (float) ((
ImageIn[col - 1][lin - 1] +
2 * ImageIn[col ][lin - 1] +
ImageIn[col + 1][lin - 1] -
ImageIn[col - 1][lin + 1] -
2 * ImageIn[col ][lin + 1] -
ImageIn[col + 1][lin + 1] ));
else
SobelY[col][lin] = 0;
if (GradientX)
SobelX[col][lin] = (float) ((
ImageIn[col - 1][lin - 1] +
2 * ImageIn[col - 1][lin ] +
ImageIn[col - 1][lin + 1] -
ImageIn[col + 1][lin - 1] -
2 * ImageIn[col + 1][lin ] -
ImageIn[col + 1][lin + 1] ));
else
SobelX[col][lin] = 0;
// Normalize and take absolute value
}
for (lin = 1; lin < draw_h - 1; lin++)
for (col = 1; col < draw_w - 1; col++)
Gradient[col][lin] = (float) (sqrt (
SobelX[col][lin] *
SobelX[col][lin] +
SobelY[col][lin] *
SobelY[col][lin] ));
for (lin = 1; lin < draw_h - 1; lin++)
for (col = 1; col < draw_w - 1; col++)
Direction[col][lin] = (float) (atan2 (
SobelY[col][lin], SobelX[col][lin]) / 3.14 * 180);
for (lin = 1; lin < draw_h - 1; lin++)
for (col = 1; col < draw_w - 1; col++)
if (Gradient[col][lin] > MaxColorGrey)
ImageWork[col][lin] = MaxColorGrey;
else
ImageWork[col][lin] = (unsigned char) Gradient[col][lin];
PlaceToImageIn();
return 0;
}
//********************************************************************************
// THESHOLD
int ImageThreshold(void)
{
unsigned int
Count, Thres, lin,col;
unsigned char
point;
ImageCreate(Area1);
for (lin = 0; lin < draw_h; lin++)
for (col = 0; col < draw_w; col++)
ImageWork[col][lin] = 0;
Thres = Threshold;
//Found threshold automatic
if (Thres == 0)
{
Count = 0; Thres = 0;
for (lin = 0; lin < draw_h; lin++)
for (col = 0; col < draw_w; col++)
if (ImageIn[col][lin] > 0)
{
Thres = Thres + ImageIn[col][lin];
Count++;
}
Thres = (unsigned int) (Thres / Count);
}
// filter the image and store result in output array
for (lin = 0; lin < draw_h; lin++)
for (col = 0; col < draw_w; col++)
{
// Apply operator
if (ImageIn[col][lin] < Thres)
point = 0;
else
point = MaxColorGrey;
ImageWork[col][lin] = point;
}
PlaceToImageIn();
return 0;
}
//************************************************************************************
//COLOR FILTER
int color_filter(int filter, int color)
{
int
res, average, r, g, b;
r = color & 63488; g = color & 1984; b = color & 31;
if (filter == filter_r)
res = r;
else if (filter == filter_g)
res = g;
else if (filter == filter_b)
res = b;
else if (filter == filter_grey)
{
r = r >> 11;
g = g >> 6;
average = ( r + g + b) / 3;
r = average;
r = r << 11;
g = average;
g = g << 6;
b = average;
res = r | g | b;
}
return res;
}
Contato:
Tel.: +55-48-331 7552/9498 |



