
Visão Computacional
1. Representação de
imagens
2. Filtragem de imagens
3. Detecção de Bordas
4. Segmentação Simples
5. Crescimento de Regiões
6. Segmentação com
Filtros
7. Segmentação a Cores
8. Análise de Texturas
9. Análise de Texturas
Multiescalar
10. Redes Neurais
11. Morfologia Matemática
12. Convolução
13. Esqueletonização
14. Técnicas Estatísticas
15. Fractais
16. Reconhecimento de
Formas
17. Representação de
Objetos
18. Quadtrees e Octrees
19. Visão Estereo
20. Inteligência Artificial
21. Controle de qualidade
22. Robótica
23. Medicina
24. Sensoriamento remoto
Prof. Aldo von Wangenheim
Currículo...
Publicações
Pesquisa
Projetos
Ensino de Graduação
Ensino de Pós Graduação
Cursos
Prof.: Aldo von
Wangenheim
Alunos: Cássio
Lopes
Carlos Henrique Z. Pantaleão
1 –
Introdução “Geometrias”
A geometria reflete a nossa percepção da natureza, preocupando-se em tornar objetivas as nossas intuições espaciais. A geometria clássica, ou euclidiana, fornece uma primeira aproximação para a estrutura dos objetos físicos. Nesse sentido, os objetos são descritos através dos elementos básicos: o ponto, a reta, o plano, ou uma combinação destes. Muitos métodos de representação de objetos tridimensionais são baseados nas formas ideais de Platão (cilindro, esfera e cubos).
Muitos padrões naturais exibem irregularidades e complexidades tão
grandes que não podem ser adequadamente descritos com a geometria
euclidiana “clássica”. Para objetos destas classes foram
criadas “geometrias alternativas”, que utilizam outras estruturas descritivas.
De particular interesse, a Geometria Fractal é uma extensão
da geometria clássica, fornecendo métodos para avaliar e
modelar objetos de extrema complexidade. Na verdade, a geometria
fractal coloca em xeque a noção de complexidade, é
um convite a olhar a natureza sob outra ótica.
2 –
A Primeira Crise: “O Problema Dimensional”
Dimensões são parâmetros que descrevem a estrutura
dos objetos/conjuntos. De acordo com a natureza dos objetos,
associa-se, classicamente, quantidades como comprimento, área e
volume, de acordo com o número de dimensões que o objeto
em questão possui.
Intuitivamente, a dimensão de um espaço métrico (ou conjunto) é igual ao número de parâmetros Reais (coordenadas) necessários para endereçar unicamente um elemento deste espaço, a partir de um elemento do conjunto tomado como referência (a “origem”). Neste contexto, um ponto possuiria dimensão 0. A Reta possuiria dimensão 1, pois apenas uma coordenada é necessária para endereçar cada ponto sobre a mesma. O Plano possuiria dimensão 2, pois são necessárias duas coordenadas para descrever um elemento deste conjunto. Generalizando, o Espaço Euclidiano Rn é n-dimensional.
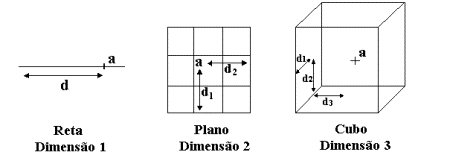
Figura 1 – Ilustração do conceito de dimensão
do Espaço Euclidiano Rn, onde
uma reta possui dimensão 1, um plano dimensão
2 e um cubo dimensão 3.
A Figura 1 ilustra a noção citada: uma curva pode ser totalmente
descrita a partir do “comprimento” percorrido sobre a mesma, partindo-se
de um ponto de referência (o ponto “a”). O mesmo princípio
aplica-se para uma superfície ou para um objeto “sólido”,
apenas aumentando-se o número de coordenadas necessárias
para descrevê-los.
2.1. – A Crise Intuitiva
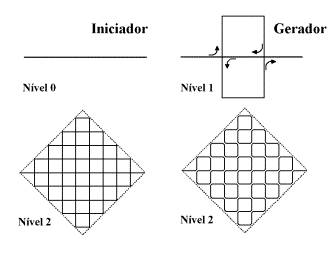
Figura 2 – Ilustração do processo de construção
da curva de Peano.
O processo de geração da curva é iterativo: partindo-se
de um segmento de reta qualquer (“nível 0”) com comprimento unitário,
divide-se o mesmo em três partes, construindo na porção
central uma espécie de retângulo (“nível 1”).
Pode-se observar que cada “lado” da figura resultante (“nível 1”)
pode ser visto como uma versão rotacionada e escalada do segmento
inicial (“nível 0”). Uma vez que se trata de um processo
iterativo, o passo seguinte é justamente realizar a operação
inicial em cada lado da curva “nível 1”, chegando na curva “nível
2”. O processo é repetido até que todo o plano
seja preenchido.
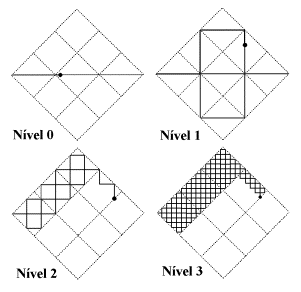
Figura 3 – Ilustração do fenômeno
de mapeamento do espaço
euclidiano explicado através da curva de Peano.
A Figura 3 demonstra o fenômeno do mapeamento: primeiramente, mede-se um ponto qualquer sobre o segmento de reta inicial (que está no R1 ), por exemplo, um ponto que esteja a 10/27 avos da extremidade esquerda, tomada como referência. Este é o ponto do intervalo unitário (já que o segmento possui comprimento total igual a 1) que será mapeado em um ponto do R2 (no plano).
No passo seguinte, realiza-se a transformação já descrita, gerando-se a curva “nível 1” (agora já contida no plano). Realiza-se a mesma medida: a partir do mesmo ponto de referência (a extremidade esquerda) percorre-se a distância de 10/27 avos do comprimento total da curva “nível 1”, seguindo o sentido indicado. O ponto de parada estará agora, naturalmente, no plano (R2).
Repetindo-se este processo inúmeras vezes, ou seja, realiza-se a transformação e em seguida mede-se 10/27 avos do comprimento da curva no estágio em questão, é possível verificar que o ponto tende a se estabilizar em um local do plano. Conforme se aumenta o número de iterações do processo, o ponto de parada converge gradativamente para um determinado local no plano. Esse ponto pode ser considerado um ponto do R2, descrevendo-o a partir de duas coordenadas (x e y, por exemplo). Entretanto, ao mesmo tempo também pode ser endereçado com uma única coordenada, partindo-se do ponto de referência (extremidade esquerda) e medindo-se 10/27 avos do comprimento total da curva no estágio em questão. Isso é válido para qualquer estágio, para qualquer iteração do processo. Matematicamente o que foi feito é um mapeamento do ponto 10/27 do intervalo unitário em um ponto correspondente do R2 . Uma vez que é possível repetir o processo para qualquer ponto do intervalo, digamos 1/12 avos, é possível mapear todo o intervalo unitário no R2 .
Em 1908 David Hilbert também propôs uma curva que mapeia o
intervalo unitário [0,1] no “quadrado unitário” [0,1] x [0,1].
O processo de geração da curva de Hilbert também é
iterativo, e o mapeamento é feito da mesma forma que na curva de
Peano. A Figura 4 ilustra a situação.

Figura 4 – Ilustração do fenômeno
de mapeamento do espaço
euclidiano através da curva de Hilbert.
3 –
Segunda Crise: Complexidade
Existem alguns objetos geométricos que são tão complexos,
que as medidas clássicas de comprimento, área ou volume perdem
o sentido.
3.1 - Um Exemplo Teórico: A Curva de Koch
QUEM FOI KOCH?
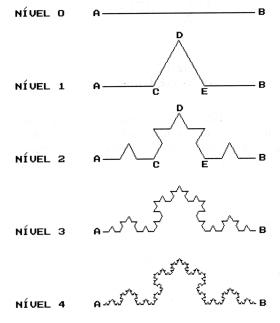
Figura 5 – Processo iterativo de construção
da curva de Koch
apresentado através dos 5 primeiros níveis.
Nível 0: L=1 (por exemplo)
Nível 1: =4/3
Nível 2: L=4*4*(1/3)*(1/3)=16/9
Nível 3: L=4*4*4*(1/3)^3=64/27
Nível k: L(k)=(4/3)k
A Figura 5 descreve o processo de geração de uma curva conhecida como “Curva de Koch”, em homenagem ao seu criador. Partindo-se de um segmento de reta de comprimento unitário, divide-se o mesmo em três partes, substituindo a parte central por uma espécie de “V” invertido. É fácil verificar que o comprimento da curva resultante, por construção, será 4/3. Cada “lado” da curva pode ser visto como uma versão rotacionada e escalada do segmento inicial, podendo-se aplicar novamente o processo descrito. A cada estágio do processo iterativo, o comprimento aumenta de um fator 4/3, assim, no estágio “k”, o comprimento total da curva será L(k)=(4/3)k . Ora, repetindo-se indefinidamente o processo, que matematicamente equivale a k tendendo ao infinito, o comprimento tende ao infinito, mas isso sem extrapolar os limites da figura: a curva tende a um comprimento infinito mas ocupando uma porção finita e bem delimitada do plano. Como seria possível, na Curva de Koch, endereçar um ponto qualquer como foi feito na Figura 1 (endereçar um ponto da curva medindo-se o comprimento necessário para chegar até ele a partir do ponto de referência)? Não é possível ! Uma vez que o comprimento total da curva (na condição limite) é infinito, qualquer porção desta também possuirá comprimento infinito.
3.2 – Um Exemplo “Prático”: O Efeito Richardson
Foi descrito uma curva “artificial” para mostrar que as medidas clássicas, como o comprimento, podem perder o sentido. No entanto esse fenômeno também pode ser observado na natureza.
Qual
é o Comprimento de um círculo cujo diâmetro é
1000 km?
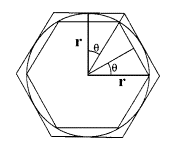
Figura 6 – Ilustração do cálculo
do perímetro de um círculo
utilizando-se um compasso de abertura ajustável.
Tabela 1 – Cálculo do perímetro do círculo
mostrado na Figura 6
utilizando-se valores diferentes de abertura do compasso.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A idéia neste exemplo é medir o comprimento de um círculo a partir de um compasso, usando-o como uma “ régua” de comprimento ajustável. Escolhendo-se uma medida inicial arbitrária para a abertura do compasso, conta-se, a partir de um ponto de referência, o número de vezes que é necessário deslocar o compasso de maneira a cobrir toda a circunferência.
Esse processo fornece uma medida aproximada do comprimento do círculo.
Caso se queira aumentar a precisão da medida, basta aumentar a precisão
do instrumento de medida: diminuir a abertura do compasso.
A Tabela 1 da Figura 6 demonstra o esperado: à medida que se diminui
a abertura do compasso, que equivale a aumentar a precisão da medida,
o comprimento tende ao valor teórico:pi×d.
Quão
Longa é a Costa da Grã-Bretanha?
O processo utilizado para medir o comprimento do círculo também
pode ser estendido para outras figuras, como a costa da Grã-Bretanha.
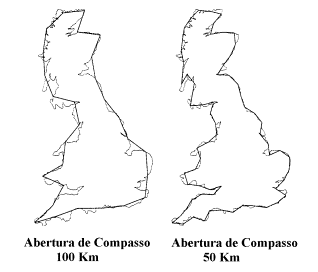
Figura 7 – Ilustração de como medir o comprimento
da costa da
Grã-Bretanha, utilizando-se um compasso de abertura
ajustável.
Tabela 2 –
Cálculo do comprimento da costa da Grã-Bretanha
tomando-se diferentes de abertura do compasso.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
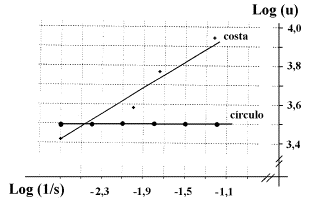
Figura 8 – Diagrama “log-log” da relação entre o comprimento total do objeto (log u)
pelo comprimento da abertura do compasso (log 1/s), utilizando-se os exemplos do
cálculo do perímetro do círculo e do comprimento da costa da Grã-Bretanha.
Denominando “u” o comprimento do objeto, e “s” o comprimento do instrumento de medida empregado, a lei que descreve o Efeito Richardson é :
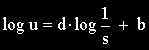
4 –
Fractais: A Geometria “entre” Dimensões
4.1 - O Que São Fractais?
“Nuvens não são esferas, montanhas não são
cones, o litoral não é um círculo e tampouco um relâmpago
viaja em linha reta pelo ar” Mandelbrot 1983
O que são fractais? Não existe uma definição “fechada”;
“São objetos geométricos irregulares com estruturas infinitamente definidas em todas as escalas”;
“São formas geométricas fragmentadas que podem ser divididas em partes, e cada parte é uma cópia escalada do todo”;
“Um conjunto
de pontos cuja dimensão fractal excede sua dimensão topológica”;
Na “geometria determinística”, as estruturas são definidas,
comunicadas e analisadas com o auxílio de transformações
tais como as transformações afins, escalamentos, rotações
e congruências.
Um
conjunto fractal, ou simplesmente, um “fractal”,contém infinitos
pontos cuja organização é tão complicada que
não se torna possível descrever o conjunto especificando
diretamente onde fica cada ponto no fractal. Ao invés,
o conjunto pode ser definido pela “relação entre as partes”.
É como descrever o sistema solar citando a Lei da Gravitação
e definindo as condições iniciais.
Redefiniu-se
a idéia: a dimensão fractal de um conjunto é
um número que diz o quão densamente um conjunto ocupa o espaço
métrico em que ele existe.
4.2
- O Parto dos Monstros: Exemplos de Fractais
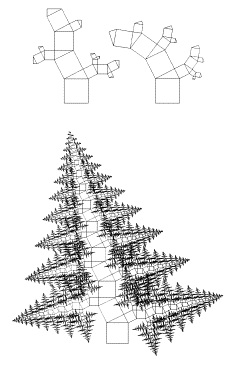
Fractais “Pitagóricos”
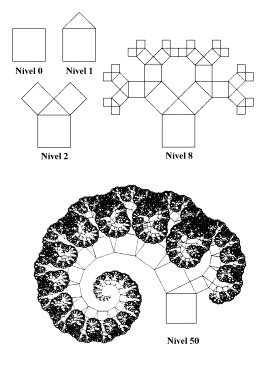
Figura 9 – Ilustração de fractais pitagóricos,
dando uma idéia
básica de geração de fractais através
do processo iterativo.
O Triângulo de Sierpinski

Figura 10 – Ilustração do processo iterativo
de
construção do Triângulo de Sierpinski
.
Conjuntos de Júlia
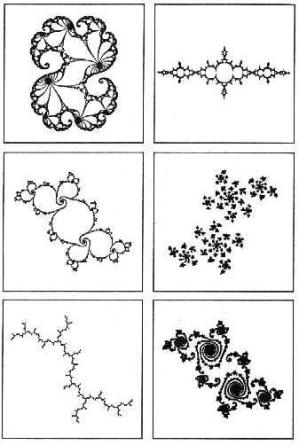
Exemplos Mais Elaborados:


4.3
- Exemplos Naturais
Objetos “naturais” não são fractais, mas são muito bem descritos por eles;
Fractais são gerados através de equações recursivas;
Atratores
Estranhos (dinâmica caótica) são fractais;

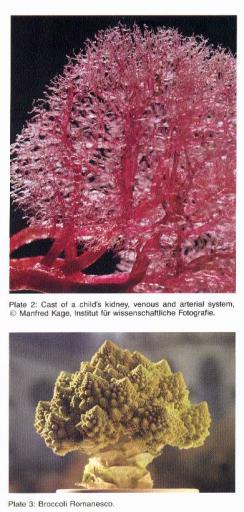
4.4
– Dimensão Fractal
Felix Hausdorff propôs o conceito de dimensões fracionárias em 1919;
Indica com precisão a complexidade de um objeto;
Estende a dimensão topológica (euclidiana)
Inúmeras definições possíveis. Destaque para:
Dimensão de Auto-similaridade;
Dimensão
“Box-counting”;
4.4.1
– Dimensão de Auto-Similaridade
Tomando-se um objeto que reside no espaço euclidiano de dimensão topológica D, escalando-o linearmente por um fator s em cada direção espacial, sua medida (comprimento, área, volume, etc) é modificada de a vezes em relação ao tamanho original:
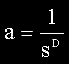
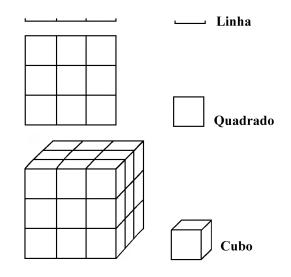
Figura 11 – Ilustração da auto-similaridade
da
linha, do quadrado e do cubo.
Tabela 3 – Ilustração da relação entre o
número de partes divididas (a) versus o fator
de escalonamento (s) para quatro tipos de objetos.
|
|
|
|
|
Linha Linha |
6 173 |
1/6 1/173 |
|
Quadrado Quadrado |
36 = 62 29.929 = 1732 |
1/6 1/173 |
|
Cubo Cubo |
216 = 63 5.177.717 = 1733 |
1/6 1/173 |
|
Curva de Koch Curva de Koch |
16 4K |
1/9 1/3K |
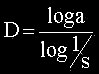
4.4.1
– Dimensão “Box Counting”
Aplicável a qualquer estrutura (estruturas que não são auto-similares);
Facilmente extraída das imagens;
Baseia-se também no Efeito Richardson.
A dimensão
é dada pela inclinação da melhor reta no diagrama
log-log.
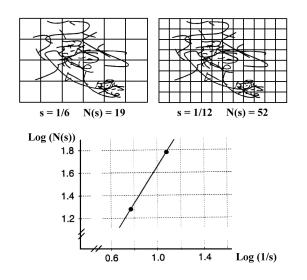
Figura 12 – Ilustração da aplicação da técnica da Dimensão Box-Counting.
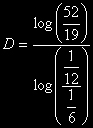 = ~ 1,45
= ~ 1,45
PROCURAR
A DEFINIÇÃO FORMAL DE DIMENSÃO “BOX-COUNTING”
5 –
Geração de Fractais
5.1
– Iterated Function Systems - IFS
Um pouco de formalismo:
Espaços Métricos.
Distância de Hausdorff.
Operador de Hutchinson.
Princípio Contratividade: Auto-contração dos Espaços Métricos.
Fractais são gerados a partir de equações recursivas;
Fractais são subconjuntos gerados por transformações geométricas simples do próprio espaço métrico em si mesmo (auto-contração);
Mapeamentos Não-lineares: Mandelbrot
Mapeamentos Afins: IFS
Rotações, translações, escalamentos:
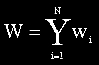
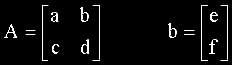
Uma vez definida a transformação (matrizes A e b), o Atrator
(figura final) é sempre o mesmo! O Atrator não
depende da figura inicial (“condição inicial”);
Exemplo
1: A Curva de Koch a partir de IFS
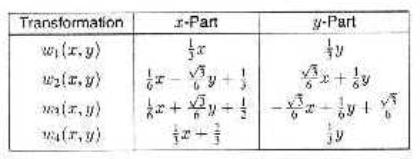
O Efeito das Transformações Afins W1, W2, W3 e W4 sobre um linha inicial (Gerador):
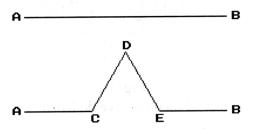
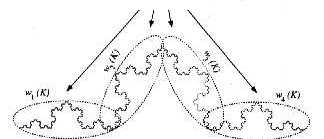
Conforme
citado, o Atrator não depende da inicialização:
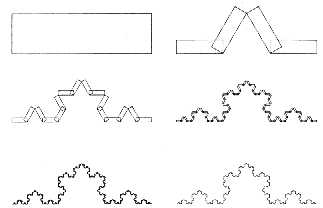
Outro
Exemplo: A Samambaia de Barnsley:

6 –
O Problema Inverso
Como
definir uma transformação cujo Atrator é um conjunto
(imagem) dado?
6.1 – “Teorema da Colagem”
Barnsley
et al. UC San Diego (INS)
Como codificar uma imagem através de fractais? Os IFS’s são
a resposta a essa questão. O insight fundamental de Mandelbrot de
que as formas prevalecentes da natureza resemble self-similar fractals
e o insight de Barnsley de que é possível pegar uma forma
(shape) e determinar um sistema dinâmico cujo atrator parece com
o shape inicial: começa-se com o fractal (imagem) e procura-se por
um IFS ou outro sistema dinâmico que convirja para o fractal inicial.
É o chamado PROBLEMA INVERSO da geometria fractal:
como achar um IFS associado a uma imagem?
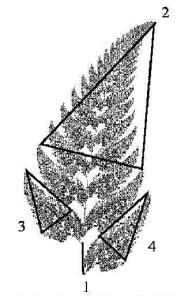

7 –
Aplicações para Fractais
Em diversos campos da ciência e da tecnologia encontram-se inúmeras
aplicações em potencial da geometria fractal, tais como na
matemática, física, química, biologia, etc..
Muitos objetos de tais aplicações, de formas extremamente
irregulares, interrompidas e aleatórias, ou seja, de conotação
com desordem, não se enquadram em modelos da geometria clássica,
devido serem aproximações úteis para se modelar objetos
reais, porém esta geometria não pode prover um modelo completo
para um objeto. Assim, entre as inúmeras aplicações
pode-se citar:
- compressão de arquivos;
- filtragem de sinais e imagens;
- segmentação de imagem;
- modelamento;
- codificação;
- reconhecimento de padrões;
- contorno e ramificações das nuvens;
- variação das populações;
- oscilações do coração;
- reconhecimento de padrões;
- e de um modo geral,
as formas irregulares e incertas.
7.1
– Aplicações da Técnica Fractal como Ferramenta para
Auxílio ao Diagnóstico Médico:
- Análise fractal
do crescimento de tumores cerebrais in vitro;

A técnica fractal é aplicada com o objetivo de analisar o
crescimento de tumores in vitro, e com isso determinar a dimensão
fractal em diferentes escalas. Pode-se constatar que existem
parâmetros de auto-similaridade nestas escalas, levando os pesquisadores
a concluir que esta técnica pode auxiliar a detecção
de tumores mesmo em sua fase inicial.
- Aplicação
da técnica fractal para análise da textura da pele;

Imagem Original Aplicação da T.L. Dimensão Fractal
Após a aquisição da imagem da pele, é aplicada
a transformada de laplace para realçar os contornos da imagem e
logo em seguida é determinada a dimensão destes contornos.
Assim, este trabalho tem como objetivo aplicar a técnica de fractais
para detecção de patologias na pele através da análise
da dimensão fractal.
- Zoom
Fractal;

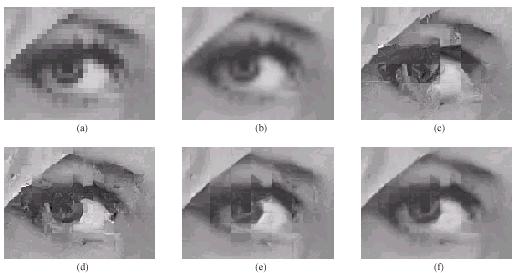
A técnica de zoom fractal está sendo muito utilizada com
o objetivo conseguir uma aproximação da imagem com o mínimo
de perdas na qualidade da imagem. A figura acima ilustra a
comparação de várias técnicas de zoom fractal,
sendo que cada uma delas apresenta valor de fator, e com isso qualidades
diferentes.
- Cálculo
da dimensão fractal da irregularidade do contorno de células
e estruturas que formam os tumores malígnos;
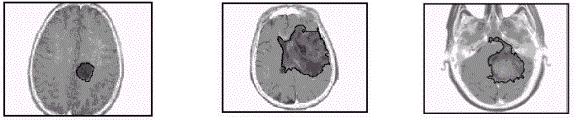
Detecção de um cisto Glioblastoma Lesão Massiva
O propósito desta pesquisa, também usando o conceito de dimensão
fractal, é de caracterizar a que estágio se encontra o os
tumores malignos no sistema nervoso central. As imagens foram
adquiridas através de ressonância magnética, das quais
foram comparadas imagens de cistos (tumores benignos), imagens de gliomas
(tumores malignos) e imagens de lesões massivas. Concluiu-se
que, com a técnica da dimensão fractal, pode-se obter uma
melhor diferenciação entre tumores benignos dos malignos
pelo fato destes últimos possuírem característica
marcante através de maior irregularidade em seu contorno.
Assim, extraindo-se a dimensão fractal destes contornos, pode-se
classificar os tumores malignos dos benignos e, posteriormente, o estágio
em que se encontra os tumores malignos.
Entre
muitos outros trabalhos utilizando a técnica fractal pode-se destacar:
- Análise fractal
do contorno ósseo e contorno dental através de imagens radiográficas;
- Cálculo da dimensão
fractal de células cancerígenas para identificação
de risco de câncer de mama. Detecção
de micro-calcificação;
- Outras investigações
fractais através de imagens de resonância magnética,
ultrasom, doppler e tomografia computadorizada;
Exemplos de Imagens Fractais
geradas por sistemas dinâmicos complexos

8
- BIBLIOGRAFIA
[1] – SERRA, Celso Penteado e KARAS, Elizabeth Wegner; “FRACTAIS GERADOS POR SISTEMAS DINÂMICOS COMPLEXOS”, Editora Champagnat, 190 p.,Curitiba – PR, 1997.
[2] – MANDELBROT, Benoît; “OBJECTOS FRACTAIS; FORMA, ACASO E DIMENSÃO”, 1a Edição, Gradiva Publicações LTDA, 296 p.,Portugal, 1991.
[3]
– PEITJEN, Heinz-Otto; JÜRGENS, Hartmut and SAUPE, Dietmar; “FRACTALS
FOR THE CLASSROOM; PART ONE – INTRODUCTION TO FRACTALS AND CHAOS”,
National Council of Teachers of Mathematics – NCTM, Springer-Verlag, 452
p., New York, 1992.
[4] – RESENDE, Ana Caroline Matias; “UM ESTUDO DO PROCESSO DE COMPRESSÃO DE IMAGEM POR FRACTAIS”, Dissertação de Mestrado, Universidade Federal de Uberlândia - UFU, 86 p., Uberlândia - MG, Julho - 1996.
[5]
– ZASLAVSKY, G.M.; SAGDEEV, R.Z.; USIKOV, D.A. and CHERNIKOV, A.A.; “WEAK
CHAOS AND QUASI-REGULAR PATTERNS”, Cambridge Nonlinear Science Series
– 1, Cambridge University Press, 253 p., New York - USA, 1991.
[6]
– McCAULEY, Joseph L.; “CHAOS, DYNAMICS AND FRACTALS – AN ALGORITHMIC
APPROACH TO DETERMINISTIC CHAOS”, Cambridge Nonlinear Science Series
– 2, Cambridge University Press, 323 p., New York - USA, 1993.
[7]
– NAKAMURA, Katsuhiro; “QUANTUM CHAOS – A NEW PARADIGM OF NONLINEAR
DYNAMICS”, Cambridge Nonlinear Science Series – 3, Cambridge University
Press, 208 p., New York - USA, 1993.
[8]
– BAKER, Gregory L. and GOLLUB, Jerry P.; “CHAOTIC DYNAMICS – AN INTRODUCTION”,
Second Edition, Cambridge University Press, 256 p., New York - USA, 1996.
[9]
– OTT, Edward; “CHAOS IN DYNAMICAL SYSTEMS”, Cambridge University
Press, 385 p., New York - USA, 1993.
[10]
– MOON, Francis C.; “CHAOTIC AND FRACTAL DYNAMICS – AN INTRODUCTION
FOR APPLIED SCIENTISTS AND ENGINEERS”, John Wiley & Sons – Inc.,
508 p., New York - USA, 1992.
[11] – FIEDLER-FERRARA, Nelson e PRADO, Carmen P. Cintra do; “CAOS – UMA INTRODUÇÃO”, Editora Edgard Blücher LTDA, 402 p., São Paulo - SP / Brasil, 1994.
[12]
– FALCONER, Kenneth; “FRACTAL GEOMETRY – MATHEMATICAL FOUNDATIONS AND
APPLICATIONS”, John Wiley & Sons LTD, 288 p., Chichester - England,
1990.
[13]
– BARNSLEY, Michael Fielding; “FRACTALS EVERYWHERE”, Second Edition,
Academic Press Professional, 531 p., Cambridge - USA, 1993.
[14]
– ‘’Fractal
and Medicine”, Lancet, 12/7/91, Vol. 338, Edição
8780, p1425, 2p.
[15]
– Bosch, Xavier;
‘’Physicists Describe New Way to Study Tumours”, Lancet,
01/2/99, Vol. 353, Edição 9146, p44, 1/2p.
[16]
– Wickware,
Potter; ‘’Computerized Image Analysis Could Help In Diagnosis”,
Dermatology Times,Aug/97, Vol.
18, Edição 8, p12, 1p.
[17]
– Polidori
and Dugelay; ‘’Zooming Using Iterated Function Systems”,
Institut EURECOM, Multimedia Communications dept, Sophia Antipolis, France.
Contato:
Tel.: +55-48-331 7552/9498 |



