
Visão Computacional
1. Representação de
imagens
2. Filtragem de imagens
3. Detecção de Bordas
4. Segmentação Simples
5. Crescimento de Regiões
6. Segmentação com
Filtros
7. Segmentação a Cores
8. Análise de Texturas
9. Análise de Texturas
Multiescalar
10. Redes Neurais
11. Morfologia Matemática
12. Convolução
13. Esqueletonização
14. Técnicas Estatísticas
15. Fractais
16. Reconhecimento de
Formas
17. Representação de
Objetos
18. Quadtrees e Octrees
19. Visão Estereo
20. Inteligência Artificial
21. Controle de qualidade
22. Robótica
23. Medicina
24. Sensoriamento remoto
Prof. Aldo von Wangenheim
Currículo...
Publicações
Pesquisa
Projetos
Ensino de Graduação
Ensino de Pós Graduação
Cursos
Marcelo Lemes Bueno
e-mail: eletrica@itagres.com.br
Resumo: O principal objetivo de um sistema de visão computacional é o desenvolvimento de mecanismos que interpretem imagens de maneira eficiente. Desta forma a detecção de bordas é uma ferramenta extremamente importante no processo de análise de imagens. Este trabalho tem como objetivo apresentar um dos algoritmos para detecção de bordas, o detector de bordas canny.
As bordas em uma imagem é
o resultado de mudanças em alguma propriedade física ou espacial
de superfícies iluminadas. A maioria das técnicas de detecção
de bordas empregam operadores diferenciais de primeira ou de segunda ordem.
Os operadores diferenciais ressaltam os contornos das bordas mas também
amplificam o ruído da cena. Grande parte dos operadores de borda
utilizam algum tipo de suavização da imagem antes da operação
diferencial. O operador de Marr utiliza uma máscara gaussianica
convoluída com a imagem; o operador de canny também suaviza
a imagem. Isto pode atenuar as bordas fracas, onde o contraste é
pequeno.
Algoritmo Canny
O detector de bordas Canny surgiu através dos trabalhos de Marr e Hildreth. Ele é um operador gaussiano de primeira derivada que suaviza os ruídos e localiza as bordas. Para desenvolver este algoritmo, primeiramente concentraram seus estudos em bordas ideais, cuja representação pode ser feita por funções em uma dimensão (1-D). Na prática este não é um modelo exato, mas representa muito bem os efeitos causados pelos ruídos.
Considerando a função
gaussianica em uma dimensão, podemos expressar:
a primeira derivada é:
e a segunda derivada é:
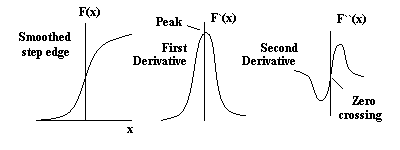
A figura abaixo mostra os
gráficos das funções de Gauss (a), a primeira derivada
(b) e a segunda derivada (c).
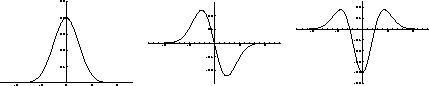 |
(a) (b) (c)
As funções
bidimensionais (2-D) são melhor expressadas em coordenadas polares
onde ![]() representa uma distância
radial da origem ao ponto. A função é simétrica
e independente de
representa uma distância
radial da origem ao ponto. A função é simétrica
e independente de ![]() . Assim,
. Assim,
a primeira derivada é
e a segunda derivada é
A figura abaixo mostra os
gráficos das funções em 2-D, de Gauss (a), primeira
derivada (b) e segunda derivada (c).
 |
(a) (b) (c)
De fato, a primeira derivada
da imagem convolucionada da função gaussianica,
é equivalente a imagem
convolucionada da primeira derivada da função de Gauss,
Portanto, é possível combinar os estágios de detecção e suavização em uma simples convolução em 1-D, cada convolução com a primeira derivada da função de Gauss e considerando os picos, ou com a segunda derivada considerando os cruzamentos dos zeros.
Como exemplo, a figura abaixo
compara as respostas entre um gradiente e a primeira derivada do gradiente
gaussianico para um ruído de borda. A detecção de
borda pode surgir de um simples "thresholding" dos dados da função
situada na posição 5, mas na prática a determinação
final da presença ou ausência de uma borda é mais complexo,
e é comum incluir estágios de pós processamento e
limiarização (thresholding).
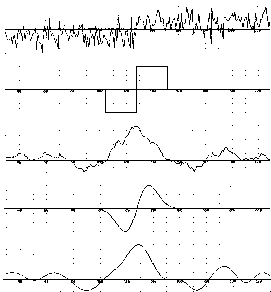 |
Comparação
entre o gradiente e a primeira derivada
do gradiente gaussiano.
O algoritmo Canny baseia-se nas seguintes regras:
- Boa detecção: Deve possuir habilidade para localizar e marcar todas as bordas realmente existentes.
- Boa localização: Minimizar a distância entre a borda detectada e a borda verdadeira (real).
- Boa resposta: Para cada borda deve haver somente uma resposta.
Estágio 1 - Uniformização da imagem
A imagem é uniformizada
por uma função gaussianica bidimensional (2-D) de tamanho
especificado por um parâmetro usual. Na prática, convoluções
gaussianicas bidimensionais de tamanho elevado, levam muito tempo para
serem processadas, portanto é comum aproximá-las por duas
funções gaussianicas unidimensionais, uma no eixo ![]() e
a outra no eixo
e
a outra no eixo ![]() . Isso
resulta em dois valores para cada pixel.
. Isso
resulta em dois valores para cada pixel.
Estágio 2 – Diferenciação
Considerando a convolução
bidimensional apresentada no estágio anterior, a imagem uniformizada
é separada nas direções ![]() e
e ![]() .
Assim é possível calcular o gradiente da superfície
uniforme da imagem convolucionada.
.
Assim é possível calcular o gradiente da superfície
uniforme da imagem convolucionada.
Considerando também
a aproximação unidimensional apresentada no estágio
1, os valores uniformizados na direção ![]() são convolucionados utilizando a primeira derivada da função
gaussianica unidimensional com mesmo alinhamento na direção
são convolucionados utilizando a primeira derivada da função
gaussianica unidimensional com mesmo alinhamento na direção ![]() .
Da mesma maneira, os valores uniformizados na direção
.
Da mesma maneira, os valores uniformizados na direção![]() são convolucionados utilizando a primeira derivada da função
gaussianica unidimensional com mesmo alinhamento, agora na direção
são convolucionados utilizando a primeira derivada da função
gaussianica unidimensional com mesmo alinhamento, agora na direção ![]() .
.
Para somar os valores dos
gradientes de ![]() e
e ![]() ,
a magnitude e o ângulo da inclinação podem ser calculados
através da hipotenusa e arctg do ângulo, similarmente ao operador
de Sobel.
,
a magnitude e o ângulo da inclinação podem ser calculados
através da hipotenusa e arctg do ângulo, similarmente ao operador
de Sobel.
Estágio 3 – Omissão de pontos de mínima intensidade
Encontrado a medida da intensidade de cada ponto da imagem, precisa-se localizar agora as bordas. Isso é possível localizando os pontos de máxima intensidade, ou de maneira inversa, pelos pontos de mínima intensidade, que precisam ser omitidos. Um valor de máxima intensidade ocorre no local mais alto da função gradiente ou onde a derivada da função gradiente possui valor zero. Entretanto, desejamos omitir os pontos de mínima intensidade ou pontos de mínimas direções perpendiculares com a borda.
Aproximações
são freqüentemente usadas, além da diferenciação
perpendicular para cada borda. Cada pixel em volta forma o centro de um
novo pixel na vizinhança. Interpolando os valores dos pixels ao
redor, as magnitudes dos gradientes são calculados pelos limites
das fronteiras vizinhas em ambas as direções perpendiculares
do pixel central, como mostrado na figura abaixo. Se o pixel considerado
na figura abaixo possuir valor menor do que os valores dos pixels vizinhos,
ele será omitido.
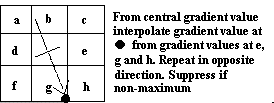 |
Estágio 4 – Limiarização da borda (threshold)
A limiarização usado no algoritmo Canny usa o método chamado "histerese".
Considerando um segmento
de borda, para todo valor situado acima do limite superior de limiarização,
ele é imediatamente aceito. Para todo valor situado abaixo do limite
inferior de limiarização, ele é imediatamente rejeitado.
Pontos situados entre os dois limites serão aceitos se eles estiverem
relacionados com pixels que apresentem respostas fortes. As figuras abaixo
mostram aplicações utilizando o operador Canny considerando
diferentes escalas e diferentes limiarizações.
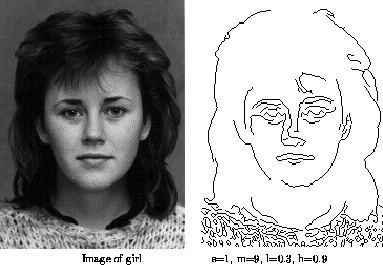 |
 |
Conclusão
O objetivo deste trabalho foi de apresentar de uma forma geral e resumida, a técnica para detecção de bordas conhecida como detector de bordas de Canny.
Referências Bibliográficas
[ 1 ] J. Canny, A computational approach to edge detection, IEEE Transactions on pattern analysis and machine intelligence, 8(6), pp 679 – 698 (1986).
[ 2 ] R.C.Gonzalez, R.E.Woods, Digital Image Processing, Addison – Wesley publishing company, 1992.
[ 3 ] Digital Image Processing: W. K. Pratt – A Willey Intercience Publication 1991 2nd edition.
[ 4 ] Digital Image Processing: R.C.Gonzalez, Paul Wintz, Addison-Wesley Publishing Company 1987.
[ 5 ] Carme Torras, Computer
Vision Theory and Industrial Applications, Springer – Verlag, 1992.
Contato:
Tel.: +55-48-331 7552/9498 |



