Sedecias Lopes Cavalcante

Departamento de Informática e Estatística

Universidade Federal de Santa Catarina

Curso de Pós-graduação em Ciências da Computação

Curso de Introdução à Visão Computacional

Florianópolis - SC

E-mail: sedecias@npd.ufsc.br

29/Set/99

1. O que é um esqueleto?
2. A transformada do eixo-médio
3. Métodos morfológicos iterativos
4. Uso de contornos
5. Uso de objetos outlines – Line Following
6. Tratando o objeto como um polígono
7. Afinamento baseado na força

1. O que é um esqueleto?

Um método básico para esqueletonização é o afinamento. Afinamento é o processo de redução de uma forma para uma versão simplificada que ainda retém as características essenciais do objeto original. A versão afinada de uma forma é chamada de esqueleto.

Há três coisas que devemos manter em mente:

1. Nem todos os objetos podem ser afinados. O afinamento é útil para objetos consistindo de linhas, se elas são retas ou curvas, e não é útil para objetos tendo uma forma que inclui uma área significativa, ou seja, para o reconhecimento de padrões como letras ele funciona bem, entretanto, para formas como um crânio, já não se aplica de modo satisfatório; o resultado final da esqueletonização de um crânio não mostra uma forma simplificada de representar um crânio, ao passo que a esqueletonização de uma letra identifica claramente o objeto.
2. O que funciona como um esqueleto em uma situação pode não funcionar em todas as situações. O afinamento é normalmente um passo na preparação de imagens para futuro processamento. A natureza dos passos subsequentes frequentemente ditam as propriedades necessárias do esqueleto.
3. O afinamento é o ato de identificar o esqueleto, e não é definido pelo algoritmo usado. Particularmente, o afinamento nem sempre é um processo iterativo de redução (lançar fora) das camadas de pixels.

Possivelmente a primeira definição de um esqueleto é esta de Blum (1967) na definição da função do eixo médio (MAF). A MAF trata todos os pixels limite como um ponto origem de um "wave front". Cada um desses pixels excita seus vizinhos com um intervalo de tempo (delay time) proporcional à distância, assim ele também, torna-se parte do wave-front. As ondas passam através de cada ponto somente uma vez, e quando duas ondas se encontram, cancelam-se uma a outra, produzindo o eixo médio ou o esqueleto (a corner). O eixo médio (MA) é o locus dos corners, e forma o esqueleto (Blum diz linha de simetria) do objeto. A MAF usa ambas as informações do tempo e espaço, e pode ser invertida para voltar a imagem original. Isto é possível para implementação direta, mas é difícil: O que é necessário é converter a transformada contínua para uma discreta. Isto envolve várias aproximações envolvendo a função da distância sobre uma grade discreta. Isto permite a MAF ser aplicada para uma imagem raster, para a qual o eixo médio não está definido.

Uma forma de encontrar o eixo médio é usar os limites do objeto. Para qualquer ponto P no objeto, localiza o ponto mais fechado (closest) sobre o limite. Se aí tiver mais de um ponto limite na distância mínima, então P está sobre o eixo médio. O conjunto de todos esses pontos é o eixo médio do objeto. Infelizmente isto deve ser feito com uma resolução muito alta, ou a distância Euclidiana não será igual quando deveria ser, e os pixels serão perdidos.

A maioria dos algoritmos de afinamento são baseados na remoção repetida de camadas de pixels até não haver mais camadas para serem removidas. Aqui, temos um conjunto de regras definindo quais pixels podem ser removidos, e frequentemente alguns tipos de esquema templates-matching é usado para implementar estas regras. Freqüentemente, as regras são projetadas de forma que é fácil de dizer quando parar: quando nenhuma mudança ocorrer depois de duas passagens consecutivas através da imagem.

1. Encontrar a localização do pixel (i, j) onde os pixels na imagem I igual estes no modelo M1 da figura 1.
2. Se o pixel central não é um endpoint, e tem número de conectividade = 1, então marque este pixel para posterior remoção.
3. Repita os passos 1 e 2 para todos as localizações dos pixels iguais ao modelo M1.
4. Repita os passos 1 – 3 para o restante dos modelos em volta: M2, M3 e M4.
5. Se qualquer pixel tiver sido marcado para remoção, então remova-o colocando-o em branco.
6. Se qualquer pixel foi deletado no passo 5, então repita o processo inteiro do passo 1; caso contrário pare.

Figura 1.

a: remove pixels do topo

b: remove pixels da esquerda

c: remove pixels de baixo

d: remove pixels da direita

Figura 2.

Conjunto de modelos para pré-processamento.

Os métodos iterativos marque-e-remova vistos de longe têm em comum que eles sempre apagam pixels da camada exterior. Estes estão sobre o limite do objeto, e formam um contorno tendo a distância de zero pixels do fundo.

Um método baseado em contornos localizam o contorno externo inteiro, ou até mesmo todos os contornos, e então deleta os pixels sobre o contorno exceto aqueles necessários para a conectividade.

Figura 3. Esqueletos obtidos do uso passos do pré-processamento Stentiford combinados com o algoritmo de afinamento de Zhang-Suen e Holt’s.

O esquema essencial usado por algoritmos de afinamento baseado em contorno é:

1. Localizar os pixels de contorno.
2. Identificar os pixels sobre o contorno que podem ser removidos.
3. Remove todos os pixels de contorno mas esses no passo 2.
4. Se qualquer pixel for removido no passo 3, então repita do passo 1.

Consiste em selecionar o pixel do meio entre cada borda (Baruch 1988).

O método usa uma janela retangular que cobre o objeto a ser esqueletonizado.

O pixel esqueletal esta no centro da janela.

A próxima janela é posicionada em função do pixel esqueletal atual.

Procedimento:

Escolher um ponto a esquerda (LP) e um a direita (RP) na borda do objeto e construir uma janela com distância fixa a partir de

LP e RP.

O pixel entre LP e RP é esqueletal.

Localizar LLP e RRP na borda da janela na direção do esqueleto.

Deslocar a janela para o novo ponto (LP=LLP e RP=RRP).

Quando um pixel de fundo é encontrado dentro da janela existe uma ramificação.

Selecionar, na borda da janela o pixel anterior entre LLP e RRP como LRP e o pixel posterior ao pixel de fundo como RLP.

Recursivamente faça LP=LLP e RP=LRP...

Quando voltar faça LP=RLP e RP=RRP (do ponto ramificado).

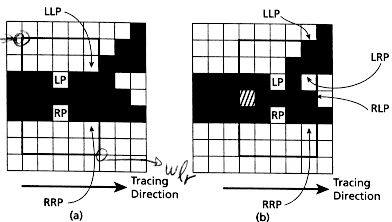
Figura 4. Afinamento por traçado de linha. (a) Traçando um linha para a esquerda. Os pixels são chamados de acordo com a descrição do algoritmo, e o retângulo preto é a janela. (b) O próximo passo no sinal da linha. A janela foi movida à direita, o centro da janela anterior é marcada como esqueleto, e novos valores para LLP e RRP. A linha se ramifica nesta janela, assim LRP e RLP existem.

Em vez de se tratado como um objeto raster, o limite de uma região pode ser feito dentro de um polígono. Os métodos baseados em contornos começam desta forma, dado que uma cadeia de código é realmente uma representação de um polígono, mas então cai dentro de velhos hábitos e descarta sucessivos contornos (polígonos) até que reste o esqueleto. Uma aproximação interessante (Martinez-Perez 1987) usa as propriedades geométricas de um polígono, que representa a borda de um objeto, para localizar o esqueleto.

O primeiro passo é obter o limite do objeto representado como um polígono.

Procedimento:

• Se o ângulo entre dois vetores for menor que 180°, uma bissetriz e construída até o lado oposto do polígono.
• Senão uma linha normal é construída no final e no início dos vetores até o lado oposto do polígono.
• esqueleto inicia no vértice 1 e passa através dos pontos médios das linhas construídas.

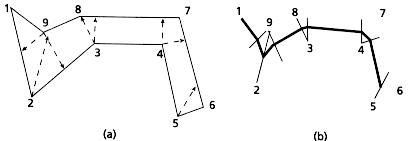
Figura 6. Tratando o objeto como um polígono. (a) Algumas das linhas projetadas calculadas para um objeto hipotético. (b) O centro das linhas são pontos sobre o esqueleto, os quais foram traçados aqui como uma linha negra espessa.

OBS: indicado para objetos finos como caracteres, gráficos, mapas...

Até este ponto, os elementos implícitos para definição do esqueleto inclui:

• Pixels de esqueleto estão em alguma sentido tão longe dos limites de um objeto quanto possível.
• Um pixel esqueleto está conectado ao menos a um outro, a menos que o esqueleto consista de exatamente um pixel.
• Uma linha cruzando os limites do objeto como uma perpendicular irá cruzar o esqueleto exatamente uma vez antes de cruzar outro limite, a menos que ele seja (a) também fechado para um ponto onde linhas se encontram, ou (b) também fechado para o fim da linha.

Definições

Uma banda digital pode ser definida como um conjunto de pixels conectados com as seguintes propriedades:

• Todos os pixels estão sem distância d perpendicular de uma curva discreta C, que não tem qualquer loops. A distância mínima entre C e qualquer pixel limite é d/2.
• O valor de d é muito menor que o comprimento da curva C.
• A direção associada com cada pixel limite é aproximadamente a mesma daquele próximo a C.

Esta definição deveria incluir a maioria das linhas e curvas digitais, grossas ou finas.

Segmento digital é um subconjunto da banda extraídos com corte perpendicular a C.

Um Fragmento é um segmento digital onde há uma brusca mudança na direção em C.

O fragmento pode ser linear, côncavo ou convexo.

Cada fragmento possui seu esqueleto, que é localizado através do cálculo da força, que os pixels de fundo adjacentes a borda, exercem sobre os pixels do objeto.

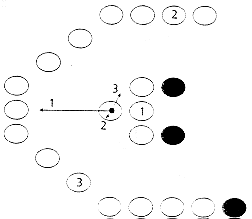
Figura 7. A força de um dado pixel é o vetor soma para todos os pixels visíveis. Somente pixels de limite exercem a força, e somente pixels objetos tem a força calculada.

Quanto mais perto o pixel objeto do pixel de fundo maior a força exercida sobre ele.

O fragmento é mapeado em quadrados e é determinado a ação da força em seus vértices.

O esqueleto cai dentro dos quadrados onde a ação da força age em direções opostas.

Estas áreas são subdivididas para o refinamento do esqueleto.

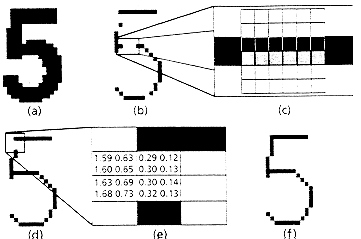
Figura 8. Subpixel skeletons. (a) A imagem original. (b) esqueleto no primeiro nível, mostrando o zero-crossing. (c) uma seção de subpixel de uma brecha no nível 0 do esqueleto. (d) O nível –1 do esqueleto. (f) O esqueleto final com todas as brechas preenchidas.

************************************************************************

Considere o caracter "I" abaixo.

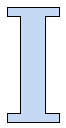
figura 9. Um modelo consistindo de três "strokes".

Isto consiste basicamente de três "strokes" ou pedaços de linha unidos (dois horizontais e um vertical) conectados de uma certa maneira. O afinamento de um "stroke" é irrelevante para o reconhecimento do problema. O que é importante é a topologia de como os três pedaços são conectados juntos. Em tais situações isto é conveniente para simplificar a entrada tanto quanto possível para fazer a análise de topologia tão simples quanto possível, i.é., em todas as iterações os pontos do objeto ou pontos pretos do objeto tendo ao menos um ponto de fundo adjacente são apagados. Mas podemos apagar um ponto de contorno se sua remoção não afetar a topologia do objeto. Uma aproximação que é bastante poderosa e popular é criar uma versão do modelo que está tão magro quanto possível. Por exemplo, seria agradável representar o modelo acima como um pixel padrão preto espesso como ilustrado abaixo.

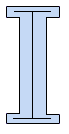
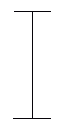
Figura 10. O modelo do esqueleto, i.e., a representação emagrecida do modelo original que preserva a topologia.

Métodos para acompanhar isto são chamados de técnicas de afinamento ou esqueletonização e os modelos resultantes são normalmente referidos como esqueletos.

Embora os limites de um objeto bi-dimensional dêem as informações completas sobre a forma do objeto, esta pode não ser a informação mais adequada para combinar. Particularmente para formas que podem ser pensadas como uma longa união, algumas vezes pequenas partes chamadas "strokes", a essência da forma pode ser descrita com uma seqüência de segmentos de linha que capturam a linearidade dos "strokes". A figura 1 mostra um conjunto de caracteres e os segmentos de linha que podem ser usados para caracterizá-los. Blum (1973) and Blum and Nagel (1978) definiu a transformada do eixo de simetria (symmetric axis transform) de um objeto bi-dimensional como um conjunto de "maximal circular disks" que cabe dentro do objeto. O objeto pode ser representado por seu eixo simétrico mais o conjunto da distância destes centros para os limites do objeto. A figura 12 dá o eixo simétrico dos caracteres na fig 11 um outro objeto bi-dimensional. O eixo simétrico é um exemplo de uma descrição do esqueleto de um objeto bi-dimensional.

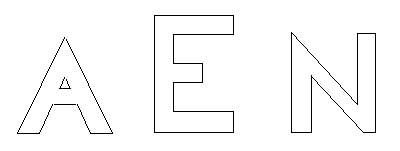
Figura 11. Segmentos de linhas que caracterizam o "strokes"de um conjunto de caracteres.

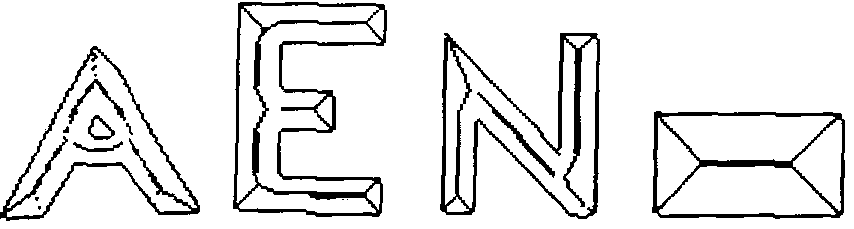
Figura 12 Eixo simétrico dos caracteres da Fig. 11 e outra forma

• eixo simétrico nem sempre é completamente o representante dos "strokes" de um objeto. Observe que o eixo simétrico de um retângulo, em lugar de ser uma única linha, consiste em cinco segmentos de linha. Esta propriedade e o fato de que o eixo simétrico é extremamente sensível ao ruído torna-o difícil de usar. Para resolver este problema, Brady and Asada (1984) desenvolveram uma definição separada para esqueleto chamada de eixo de simetrias locais suaves (axis of smoothed local symmetries). Uma simetria local é o ponto central P de um segmento de linha BA une um par de pontos A e B no limite de uma forma tal que o ângulo a entre BA e o externo normal n_A e A, seja o mesmo que o ângulo entre BA e o interno normal n_B e B, como ilustrado na figura 13. O loci de simetrias locais que são maximal com respeito a formar uma curva suave são chamados eixos ou espinhas (axes or spines). A cobertura de um eixo é a porção da forma subtendida pelo eixo. Se a cobertura de um eixo é contida corretamente na cobertura de um segundo eixo, o primeiro eixo é sobreposto pelo segundo. A figura 14 ilustra os eixos de simetria de um retângulo. Os pequenos eixos diagonais são sobrepostos pelos eixos horizontal e vertical e podem ser deletados ou removidos para um local abaixo na descrição hierárquica da forma. A figura 15 mostra a simetria local suave (de Brady e Asada) de outros objetos.

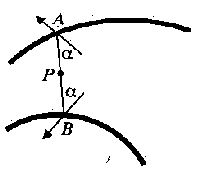
Figura 13 Um ponto P que é uma simetria local com o respeito aos limites dos pontos A e B.

Figura 14 Eixo simétrico da simetria local de um retângulo.

Figura 15 Eixo da simetria local suave de diversos objetos.

A última representação para formas bi-dimensionais é uma decomposição da área inteira de uma forma em pequenas partes de duas dimensões. As partes, seus atributos, e seus inter-relacionamentos podem ser usados para formar uma descrição estrutural da forma. A questão principal que fica é, como nós definimos as partes de uma forma?

Pavlids agarrou o problema da decomposição das formas com diversas aproximações diferentes. Uma aproximação prematura foi a decomposição de formas em subconjuntos convexos primários (Pavlids, 1968). O subconjunto convexo primário e o "nuclei" (regiões onde os subconjuntos primários se sobrepõem) formam os nós de um gráfico representando a forma original (Pavlids, 1972). A figura 16 mostra um exemplo da letra E decomposta em subconjuntos primários convexos e nuclei. Uma aproximação relacionada foi a decomposição em partes convexas, partes "T-shaped", e espirais por Feng e Pavlids (1975). Embora o segundo método relaxou os constrangimento do primeiro, ele não se dirigiu ao problema de ruído e formas deformadas.

Shapiro e Haralick (1979) projetou um método para decompor formas em pedaços próximo-convexo (near-convex pieces). A próxima-convexividade permite ruídos ou instâncias um pouco distorcidas de formas perfeitas para ter a mesma ou quase a mesma decomposição como as formas perfeitas de si mesmo. Este método calcula a relação binária que captura importantes informações acerca da forma de um objeto bi-dimensional representado como uma seqüência de pontos. A relação binária é construída como a seguir:

Dados dois pontos P₁ e P₂ sobre o mesmo limite de um objeto, podemos construir uma estreita linha de P₁ para P₂. Se a linha ficar completamente dentro dos limites do objeto, então o par ordenado (P₁ , P₂) pertence à relação L_I. A relação L_I, algumas vezes chamada de relação da visibilidade, pode ser calculada em O(n²) vezes (Lee, 1983). Uma vez que a relação foi calculada, um gráfico teórico agrupando os algoritmos que foram dados em Shapiro e Haralick (1979) determina o grupo da relação. O ponto em cada grupo define a parte próximo-convexo do objeto. A figura 17 ilustra a decomposição de diversas letras Es imperfeitas de nosso paper "structural-shape-matching" (Shapiro, 1980).

Philips (1985) decompos a forma em pedaços compactos pelo uso da forma esqueleto e o valor da distância associado à ele.

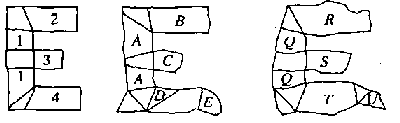
Figura 17. Decomposição de três formas similares em pedaços próximo-convexo. Aos pedaços é permitido a sobreposição.

Definindo Algumas Funções

Considere os seguintes 8 pixel vizinhos do pixel p1

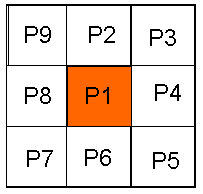
Figura 18.

Nós devemos descartar p1 ou mantê-lo como parte do esqueleto. Para este propósito nós organizamos os 8 pixels vizinhos de p1 no sentido-horário e definimos as duas funções:

B(p1) = número de vizinhos não-zero de p1

e

A(p1) = número de 0,1 modelos na sequência p2,p3,p4,p5,p6,p7,p8,p9,p2

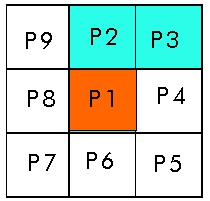
B(p1)=2 , A(p1)=1

Figura 19.

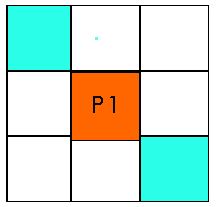
B(p1)=2, A(p1)=2

Figura 20.

Há duas versões para o algoritmo de Hilditch, um que usa uma janela 4x4 e o outro que usa uma janela 3x3. Aqui nós nos preocupamos com a versão de janela 3x3.

O algoritmo de Hilditch consiste do desempenho de múltiplos passos sobre o modelo e sobre cada passo, o algoritmo checa todos os pixels e decide mudar um pixel de preto para branco se ele satisfizer as seguintes quatro condições:

•2 < = B(p1) < = 6

•A(p1)=1

•p2.p4.p8=0 ou A(p2)!= 1

•p2.p4.p6=0 ou A(p4)!= 1

Para quando não houver mudanças (não há mais pixels para serem removidos)

Permite-nos ver cada uma das condições separadamente.

Condição 1 : 2 < = B(p1) < = 6

Esta condição combina duas subcondições, primeiro aquela que o número de vizinhos não-zero de p1 é maior que ou igual a 2 e segundo que ele pode ser menor que ou igual a 6. A primeira condição assegura que o ponto final A primeira condição assegura que nenhum pixel "end-point" não isolado seja apagado (qualquer pixel com 1 vizinho preto é um pixel end-point), a segunda condição assegura que o pixel é um pixel de limite.

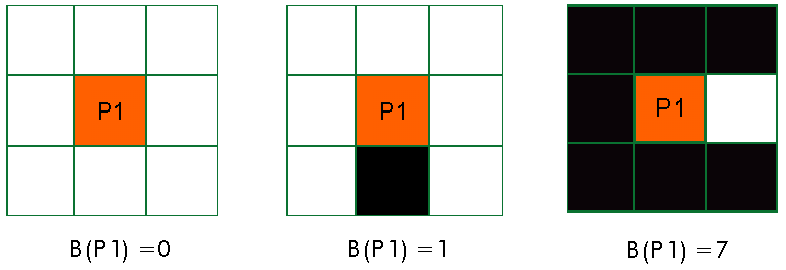
Figura 21.

Condição 2 : A(p1)=1

Isto é um teste de conectividade. De fato, se você considerar as imagens abaixo onde A(p1)>1, você pode ver que mudando p1 para 0 o padrão irá ser desconectado.

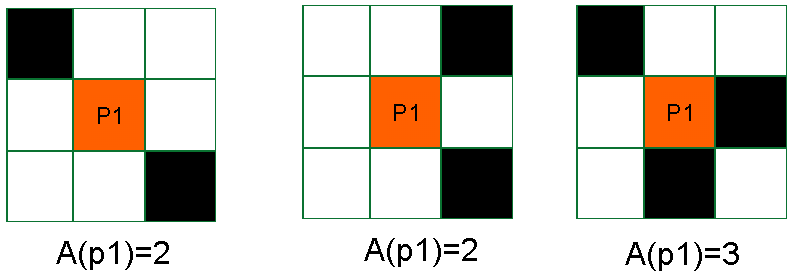
Figura 22.

Condição 3 : p2.p4.p8 = 0 ou A(p2)!=1

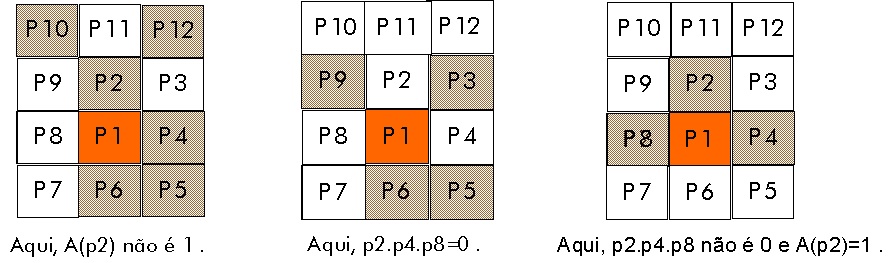
Figura 23.

Esta condição assegura que os 2 pixel da linha do lado vertical não são completamente erodidas pelo algoritmo.

Figura 24.

Condição 4 : p2.p4.p6 = 0 ou A(p4)!=1

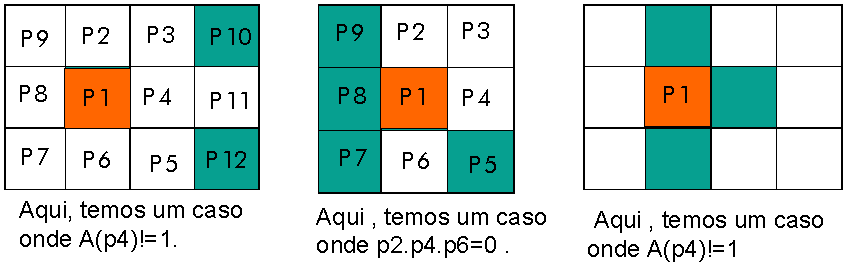
Figura 25.

Esta condição assegura que os 2 pixel da linha do lado horizontal não são completamente erodidas pelo algoritmo.

Figura 26.

É um algoritmo paralelo-seqüencial. É paralelo porque ao passar todos o pixels são conferidos ao mesmo tempo e são tomadas decisões de remover cada um dos pixels conferido. É seqüencial porque este passo há pouco mencionado é repetido várias vezes (até que nenhuma mudança seja feita)

Porém, o algoritmo de Hilditch se mostrou não ser o algoritmo perfeito para esqueletonização porque não trabalha em todos os padrões. De fato, há padrões que são completamente apagados pelo algoritmo.

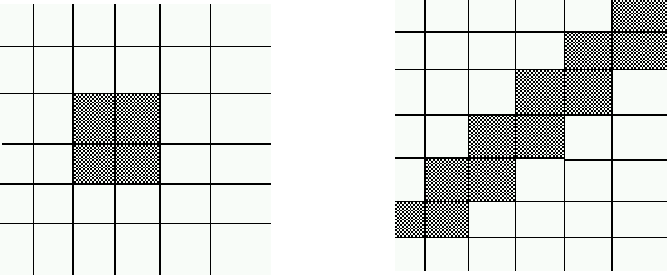
Figura 27.

Padrões que o algoritmo de Hilditch apaga completamente