Departamento de Ciências da Computação
Curso: Visão Computacional
Autor: Paulo Pizarro
Segmentação Mumford-Shah
Introdução
Uma questão central na visão computacional é a simplificação de uma dada imagem, reduzindo-se as informações dessa imagem para regiões mais ou menos homogêneas. Uma procura por partições da imagem em conjuntos finitos de áreas, onde a informação não útil da imagem original foi filtrada. Isto é conhecido como o problema da segmentação. O resultado é uma “caricatura” da realidade onde somente a parte importante está presente, sendo que os detalhes desnecessários e ruídos são extraídos. Como exemplo queremos detectar automaticamente defeitos em imagens de madeira por computador. Isto é também um dos principais interesses em aplicações industriais como controle de qualidade, inspeção automática de peças em fábricas ou visão robótica. Existem vários métodos usualmente utilizados para fazer isto, tais como eliminação de pequenas regiões, thresholding, algoritmos de expansão e compressão e filtros de frequência. Mais para várias aplicações esses métodos são muito imprecisos. Por exemplo, quando o método thresholding é aplicado para uma imagem de madeira, permanecerá uma quantidade enorme de pequenas regiões não desejáveis. Por outro lado se formos mais rigoroso nesse método, informações necessárias serão descartadas.
Imagem Original (Madeira)
Aplicado Thresholding
Segmentação Mumford-Shah
Este é um método mais preciso para a segmentação, baseado na equação funcional da energia de Mumford-Shah mostrada abaixo: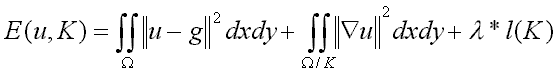
Imagem Original (Madeira)
Aplicado Mumford-Shah
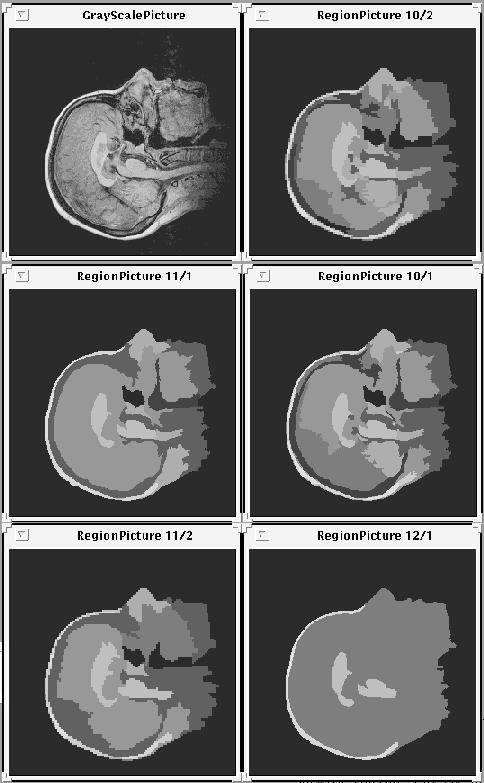
Abaixo apresentamos uma sequência de imagens segmentadas pelo método Mumford-Shah. Na primeira imagem, cada ponto representa uma região. Na primeira segmentação, os pontos vizinhos foram agrupados numa mesma região segundo o critério de menor energia. O valor do nível de cinza dos pontos desta nova região é a média dos pontos agrupados.
Equação Funcional de Mumford-Shah
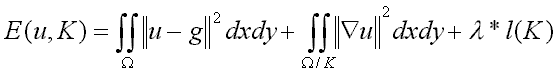
E(m,K) - Energia funcional de Mumford-Shah em função de m e da fronteira K
g(x,y) - função intensidade de luz no ponto x,y.
W - Domínio da imagem, geralmente um retângulo.
K - Fronteira entre regiões.
Wi - Decomposição da imagem em “piece-wise”.
W = W1 È W2 È ... È Wn È K
l(K) - comprimento dos arcos das bordas (fronteiras).
m(x,y) - função diferenciavél dentro de cada região Wi.
l - parâmetro de escala
A função g(x,y) é suave (valor de gradiente pequeno)
dentro de cada região Wi (piece-wise),
e é descontínua (valor de gradiente elevado) no cruzamento
com as bordas (fronteiras entre regiões).
Para o nosso caso, a função m(x,y)
será uma função constante, que é diferenciável
dentro da região. E esse valor constante será a média
dos valores de intensidade g(x,y) de cada ponto da região.
Agora vamos interpretar o significado de cada termo da equação funcional da energia de Mumford-Shah:
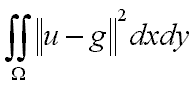Mede se m(x,y) é uma boa aproximação
de g(x,y).
Quanto melhor a função m(x,y)
se aproximar da função g(x,y), menor será a contribuição
desse termo para o valor da energia.
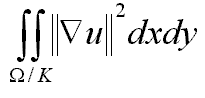Calcula a variação mínima de m(x,y)
dentro de cada região sem a borda.
No nosso caso como a função m(x,y)
será o valor média dos pontos de g(x,y) dentro da região
e portanto um valor constante, não existirá variação,
assim este termo será sempre zero.
Calcula o comprimento das fronteiras multiplicado por um parâmetro
de escala l.
Quanto maior o comprimento das fronteiras, maior será a contribuição
desse termo para o valor da energia. Ainda esse valor será multiplicado
por um parâmetro que funciona como um peso.
Energia Funcional Simplificada de Mumford-Shah
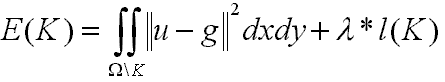
m(x,y) - Função constante dentro
de cada região e é a média dos valores de g(x,y) em
cada região. A função da energia simplificada de Mumford-Shah
fica em função apenas de K (fronteiras das regiões).
Critério de Junção
Dado duas regiões adjacentes Oi e Oj separadas por uma fronteira comum d(Oi, Oj) e o valor de energia E(m,K). Uma nova segmentação (m',K') será obtida, removendo-se a fronteira comum d(Oi, Oj) dessas duas regiões adjacentes. Esta nova segmentação:(m',K') = (m,K) \ d(Oi, Oj) é agora chamada uma subsegmentação.
Se a energia dessa nova subsegmentação for menor que a energia anterior (antes de juntarmos as duas regiões), ou seja:
E(m',K') < E(m,K)
então, é interessante a junção dessas duas regiões. Porém antes de juntarmos estas duas regiões devemos fazer o mesmo para todas as regiões vizinhas à estas duas regiões Oi e Oj e verificarmos qual é a junção que ocasionará o maior decréscimo de energia.
Caso não se encontre nenhuma região adjacente que ocasione nenhum decréscimo de energia, ou seja:
E(m',K') >= E(m,K)
então, a segmentação (m,K) é chamada de 2-normal.
Quando não for mais possível juntar nenhuma região,
deve-se aumentar o valor de lambda. O incremento de lambda poderá
ser linear ou exponencial.
Implementando o Modelo Simplificado Mumford-Shah
O critério de juntar duas regiões Oi e Oj está na dependência do sinal de E(K)\d(Oi, Oj) - E(K), no qual é apenas o decréscimo de energia. Assim a equação para o critério fica: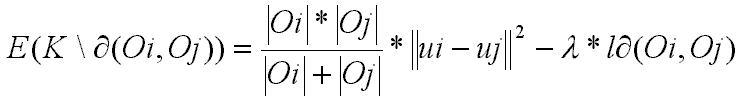
onde:
|Oi| - Área da região Oi
|Oj| - Área da região Oj
mi - valor de intensidade da região i
mj - valor de intensidade da região j
ld(Oi, Oj) - Comprimento da fronteira entre as regiões Oi e Oj
O critério foi calculado da seguinte maneira:
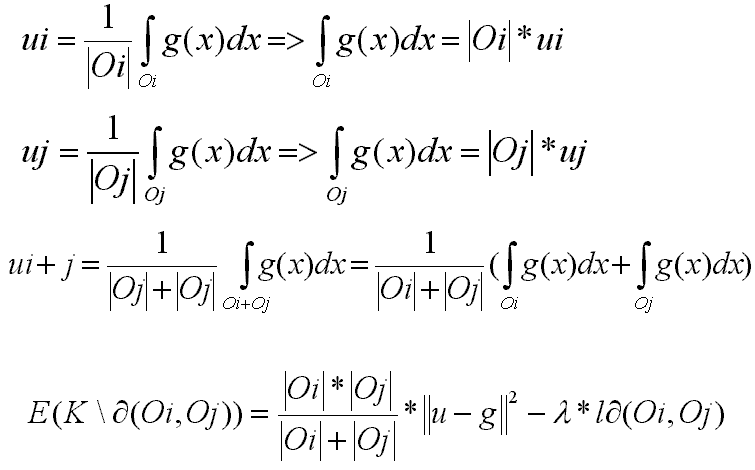
Exemplos
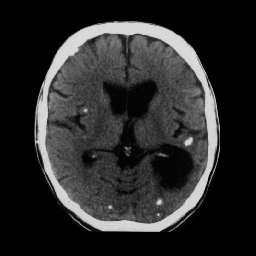
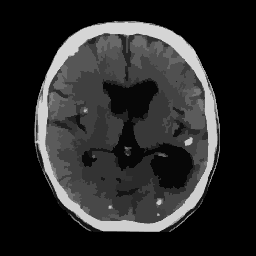
Imagem Original Lambda 1 - 800
Lambda 1 - 10.000
Lambda 1 - 100.000
Imagem Original
Lambda 1 - 800
Observação
Uma vez definida as regiões ficou fácil determinar as bordas de interesse da imagem original. Onde o valor da intensidade muda de valor é uma borda, assim pintamos esse ponto de preto, caso ele se mantenha o mesmo pintamos de branco. Assim para os exemplos anteriores temos:
