
- The Cyclops Project- CPGCC - INE -UFS
| Técnicas de Filtragem |
- The Cyclops Project- CPGCC - INE -UFS |
A área de processamento de imagens (PI) é um excelente exemplo de
interdisciplinaridade. As diversas técnicas originalmente desenvolvidas para tratamento
de sinais unidimensionais foram, em primeiro lugar, adaptadas para tratamento de imagens
obtidas de satélites e de naves espaciais. Posteriormente, com o rápido avanço das
opções de hardware e software, estas mesmas técnicas passaram a ser aplicadas em
inúmeros domínios tais como medicina, ciência dos materiais, microscopia, artes, etc...
As técnicas de filtragem são transformações da imagem "pixel" a "pixel", que não dependem apenas do nível de cinza de um determinado "pixel", mas também do valor dos níveis de cinza dos "pixels" vizinhos, na imagem original.
O processo de filtragem é feito utilizando-se matrizes denominadas máscaras, as quais são aplicadas sobre a imagem. Exemplo: a imagem original formada por uma matriz de 512 linhas por 512 colunas de valores numéricos, sendo aplicada uma máscara matricial de 3 linhas por 3 colunas. Cada valor da matriz 3x3 da máscara corresponde a um peso.
Ex: Máscara com centro na posição (2,2). 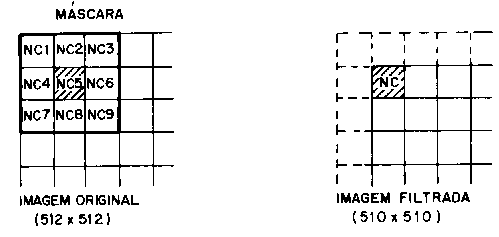
A aplicação da máscara com centro na posição (i,j), sendo i o número de uma dada linha e j o número de uma dada coluna sobre a imagem, consiste na substituição do valor do "pixel" na posição (i,j) por um novo valor, o qual depende dos valores dos "pixels" vizinhos e dos pesos da máscara.
A imagem resultante da aplicação de um filtro é uma nova imagem com a eliminação das linhas e colunas iniciais e finais da imagem original.
Os filtros espaciais podem ser classificados em passa-baixa, passa-alta ou passa-banda. Os dois primeiros são os mais utilizados em processamento de imagens. O filtro passa-banda é mais utilizado em processamentos específicos, principalmente para remover ruídos periódicos.
Joseph Fourier deixou para a matemática um rico legado:
a transformada que leva o seu nome é utilizada em diversas áreas da ciência e
tecnologia hoje em dia. Sua aplicação em PI (processamento de imagens) tem relevada
importância , desde a simples filtragem até a utilização na compressão de arquivos de
imagem. Esta transformada é uma das maneiras de realizar uma mudança de domínio
espacial em espectral ( onde um sinal fica caracterizado por suas componentes de
freqüência). Para imagens digitais (uma função bidimensional discreta), utiliza-se a
Transformada de Fourier Discreta( DFT – Discrete Fourier Transform ), que é definida
como:

Estas duas equações representam um par de transformadas. Pode-se
obter outros pares trocando o sinal das exponenciais ou então realizando a
multiplicação pela constante apenas na transformada inversa. Inclusive esta última
sugestão é recomendada para a implementação do algoritmo pois reduz o número de
operações a serem realizadas.
O termo exponencial nas equações é visivelmente separável. Fazendo com que o
somatório em x possa conter todos os termos em x, assim a equação 3-1 fica:
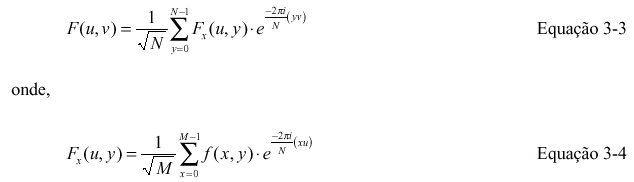
ou seja, chegamos a duas transformadas unidimensionais, uma para colunas e outra para as
linhas (a inversa tem demonstração equivalente). Esta propriedade permite com que a DFT
seja calculada em duas etapas: uma para as colunas e outra para as linhas obtidas com a
etapa anterior.Os somatórios nas equações vistas são aproximações de integrais, que
por sua vez fornecem uma medida da "densidade "da freqüência u ou v ao longo
de todo o domínio f, porém não no dá informações sobre a localização dessa
freqüência no domínio da função.Existem outras transformadas que nos levam a outros
modelos espectrais, tais como a Transformada Cosseno e a Transformada de Wavelets.
A imagem complexa resultante da DFT possui a freqüência (0,0) no
pixel de coordenada (0,0). Neste ponto a imagem atinge o seu maior valor, pois nele é
computada justamente a menor freqüência presente na imagem e pode-se deduzir que este é
o valor médio da imagem. Sabendo-se que a DFT é periódica com período N, este ponto
irá se repetir em (N, N). Estamos observando o início e o fim de um período. Contudo
para fins de análise é mais conveniente que observemos de -N/2 até +N/2, colocando a
freqüência zero no centro da imagem.
A centralização da imagem da transformada é feita de maneira muito simples, já que:
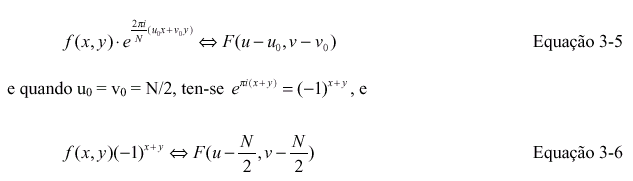
Portanto, durante o cálculo da primeira etapa podemos realizar esta multiplicação e
automaticamente obter a imagem da transformada já centrada. O problema com esta
multiplicação está no fato de que quando calcularmos a inversa obteremos a imagem
original com as multiplicações efetuadas. Assim, é necessário que estas
multiplicações sejam desfeitas no algoritmo da transformada inversa. A mudança da
origem se torna ainda mais interessante quando constatamos que a maior parte de nossas
imagens a serem processadas pela DFT são imagens reais. A DFT neste caso exibe uma
característica peculiar de simetria, onde:
F( u,v) = F* (-u,-v) Equação 3-7
Quando visualizamos o módulo da transformada temos:
|F( u,v)|=|F( u,v)| Equação 3-8
ou seja, observamos uma imagem simétrica em relação à origem. As imagens complexas
com esta característica são chamadas de hermitianas. Esta propriedade nos ajuda a
reduzir o tempo de cálculo de transformada (basta calcular a metade), e define uma das
características dos filtros deste trabalho, descritos adiante.
A DFT de uma imagem é essencialmente uma representação em série de
Fourier de uma função bidimensional. Sendo assim, para ser válida esta função precisa
ser periódica. Essa periodicidade é obtida considerando que a imagem se repete em um
plano infinito como na Figura 3-1:

Figura 3-1 Imagem Replicada em um Plano Infinito.
Esta consideração para a validade da operação justifica o
aparecimento de uma cruz central passando pela origem da imagem da transformada. São
falsas freqüências espaciais ao longo dos eixos, necessárias para a representação da
imagem dentro de uma área limitada. Estas freqüências não são prejudiciais à
reconstrução, pelo contrário são necessárias para reconstruir as bordas da imagem.
Naturalmente isso só acontece para imagens que possuam bordas laterais com intensidades
diferentes, provocando uma descontinuidade após a replicação. Caso se deseje eliminar a
cruz central para uma melhor visualização das freqüências presentes na imagem, uma
solução é aplicar uma máscara que suavize a proximidade da borda até que o valor do
pixel na mesma seja zero, eliminando a descontinuidade.
A principal propriedade da FT é dada pelo Teorema da Convolução, que
diz que a convolução entre duas funções no domínio real tem como transformada a
multiplicação das transformadas das duas funções no domínio da freqüência, ou seja:
f (x) Ä g(x) Û F(u) . G(u)
Equação 3-9
Quando consideramos g(x) como uma função que modifica f(x), a
operação de convolução no domínio real pode ser compreendida como uma filtragem. Uma
operação de multiplicação é muito mais simples do que uma operação de convolução.
Mas, para realizarmos a mesma filtragem no domínio da freqüência temos que calcular a
FT das duas funções, multiplicá-las e calcular a IFT da imagem resultante, o que
aparentemente não nos dá muita vantagem.
Transformada Rápida de Fourier
A primeira divulgação de forma ampla do algoritmo de transformada
rápida de Fourier (FFT- Fast Fourier Transform) ocorreu através do trabalho de J. W.
Cooley e J. W. Tukey em 1960, [BRIGHAM 74]. Mas, pelo menos 20 anos antes, Danielson e
Lanczos formularam uma das derivações mais claras do algoritmo, [PRESS 89].
Eles mostraram que a DFT pode ser reescrita como a soma de duas outras
DFTs, cada uma de tamanho N/2. Uma delas é formada pelos ponto pares e a outra pelos
pontos ímpares do conjunto inicial. A prova é simples:

e![]() correspondem
a k-ésima componente da DFT de comprimento N/2 formada com os componentes pares e
ímpares, respectivamente, do conjunto inicial. A grande idéia por traz desta propriedade
é que pode ser usada recursivamente até o ponto em que temos uma transformada de apenas
2 termos, que possui cálculo trivial. Assim, durante o cálculo da FFT teremos uma
progressiva mudança de dimensão da transformada: 2, 4, 8, ..., N. Obviamente N aqui é
uma potência de 2, sendo esta a maior restrição deste algoritmo. Como isto também é
válido para M, vamos impor que M=N, pois simplificará o tratamento algorítmico. O fato
de M e N serem potências de 2 enfatiza a diferença entre eles e na prática acabaríamos
trabalhando quase sempre com imagens quadradas.O principal problema aqui é saber como
combinar as transformadas de ordem 2, depois as de ordem 4, etc... A situação mais
simples que poderíamos ter é combinar pares adjacentes de elementos, depois combinar
elementos resultantes em pares também adjacentes e assim por diante. Para tanto, temos
que reordenar os elementos dessa maneira.Aplicando sucessivas divisões entre pares e
ímpares até obtermos uma transformada de 1
correspondem
a k-ésima componente da DFT de comprimento N/2 formada com os componentes pares e
ímpares, respectivamente, do conjunto inicial. A grande idéia por traz desta propriedade
é que pode ser usada recursivamente até o ponto em que temos uma transformada de apenas
2 termos, que possui cálculo trivial. Assim, durante o cálculo da FFT teremos uma
progressiva mudança de dimensão da transformada: 2, 4, 8, ..., N. Obviamente N aqui é
uma potência de 2, sendo esta a maior restrição deste algoritmo. Como isto também é
válido para M, vamos impor que M=N, pois simplificará o tratamento algorítmico. O fato
de M e N serem potências de 2 enfatiza a diferença entre eles e na prática acabaríamos
trabalhando quase sempre com imagens quadradas.O principal problema aqui é saber como
combinar as transformadas de ordem 2, depois as de ordem 4, etc... A situação mais
simples que poderíamos ter é combinar pares adjacentes de elementos, depois combinar
elementos resultantes em pares também adjacentes e assim por diante. Para tanto, temos
que reordenar os elementos dessa maneira.Aplicando sucessivas divisões entre pares e
ímpares até obtermos uma transformada de 1
termo, chegamos ao seguinte:
 |
Equação 3-12 |
onde fn não depende de k (obs.: e - even, o - odd), nos resta agora
descobrir quem é n no conjunto original. Se substituirmos os e’s e os o’s por
0’s e 1’s, respectivamente, obtemos um número binário. O valor de n é
exatamente este número com a ordem dos bit invertida. Isto é verdade porque as
subdivisões sucessivas em pares e ímpares são testes sucessivos de bits de baixa ordem
de n.
Para exemplificar isso tomemos uma transformada de 8 pontos {f(0),
f(1), f(2), f(3), f(4), f(5), f(6), f(7)}. A primeira divisão entre pares e ímpares nos
fornece dois conjuntos {f(0), f(2), f(4), f(6)} e {f(1), f(3), f(5), f(7)}. Na segunda
divisão temos quatro conjuntos {f(0), f(4)}, {f(2), f(6)}, {f(1), f(5)} e {f(3), f(7)}.
Escrevendo esta ordem na tabela podemos comparar os índices e a ordem dos bits dos
mesmos.

Tabela 3-1 Reordenação Usando a Inversão de Bits.
Portanto, o algoritmo da FFT é dividido em duas partes. Na primeira os
dados são reordenados (Bit Reversal Section) e em seguida para cada potência de 2
computam-se os valores das subtransformadas.
Este algoritmo não é nem um pouco trivial. Sua vantagem reside
justamente no tempo de processamento muitas vezes menor que o método de cálculo direto.
Isto pode ser melhor evidenciado através do conceito de Complexidade Algorítmica.
Tomando em consideração o número de multiplicações complexas, a equação 3-1 possui
NxN multiplicações, que são realizadas para todos os elementos da imagem, ou seja, NxN
pontos. Portanto, a complexidade da DFT é obviamente O(N 4 ). No caso da FFT, continuamos
possuindo NxN pontos. Mas, a subdivisão sucessiva possui complexidade O(logN), resultando
para a FFT O(N 2 xlogN), um resultado que valida todo o esforço de se implementar o
algoritmo. No fundo estamos aplicando aqui o conceito de dividir para conquistar em um
conjunto de N pontos (colunas), o que dá O(NxlogN), repetido para as N linhas,
totalizando O(N 2 xlogN).
Embora tenhamos passado por todas as etapas do algoritmo, na prática
não é utilizada a recursão e a implementação se torna complexa. Dentre os algoritmos
pesquisados existem diversas pequenas diferenças, a literatura apenas explica o
funcionamento de cada um e não como se chegou ao mesmo. Portanto, acaba-se por copiar
algum algoritmo implementado, entendendo-se como funciona mas não como deduzi-lo.
O algoritmo de FFT é feito in-place, ou seja, sobre o próprio
conjunto de dados complexos, no caso de imagens reais preencheríamos o conjunto complexo
com a parte imaginária nula e realizaríamos o cálculo. Mas, podemos ainda utilizar um
truque para o cálculo das colunas, utilizando a parte imaginária como se fosse uma
divisão entre pares e ímpares, ou seja, coloca-se os termos pares do conjunto real na
parte real do conjunto complexo e os termos ímpares na parte imaginária. Estamos então
utilizando uma transformada complexa de N pontos para calcular duas também de N pontos.
Após o cálculo temos que separar o resultado utilizando o fato de que a transformada de
um conjunto real é complexa hermitiana.
Existem ainda diversas variações do algoritmo de FFT. Quando se
realiza os cálculos primeiro e depois a reordenação o algoritmo tem o codnome de
Sande-Tukey, onde antes era Cooley-Tukey. Também pode-se acelerar o processo de cálculo
forçando N a ser uma potência de 4 ou 8, neste caso são chamados de FFT de ordem 4, 8
(quando a ordem não é especificada, assume-se ordem 2). Existem ainda algoritmos para
N=n1 x n2 x n3 ... onde os n’s são números primos. Nestes dois últimos casos é
preciso saber balancear a complexidade de implementação do algoritmo com o ganho de
performance obtido.
A DFT também pode ser obtida a partir de uma outra transformada, a de
Hartley [O’NEILL 88]. Utilizando um algoritmo semelhante ao da FFT a FHT (Fast
Hartley Transform) é mais rápida e consome menos recursos que a FFT, pois transforma
dados reais em dados também reais. A DFT 0é obtida usando as equações a seguir:

Infelizmente a FHT não foi aproveitada neste trabalho.
Mas convém ser mencionado para futuros melhoramentos.
Vimos nesta seção as diversas facetas do algoritmo de FFT e seu uso em imagens digitais.
Agora que já conseguimos chegar até a imagem complexa no domínio da freqüência,
podemos introduzir as técnicas de filtragem.
Filtragem no Domínio da Freqüência
Como explicado anteriormente, a técnica da filtragem no domínio da
freqüência é muito simples, pois equivale a uma multiplicação. Na Figura 3-2 podemos
ver uma seqüência inteira de filtragem, tanto no domínio real, como no domínio da
freqüência. Na primeira parte vemos uma senóide modelada com um ruído também
senoidal. Como a freqüência do ruído é maior que a da senóide, este se manifesta como
os dois impulsos mais externos no domínio da freqüência. Para removê-los basta aplicar
um passa baixa no domínio da freqüência, que de volta ao domínio real obteremos a
senóide sem o ruído.
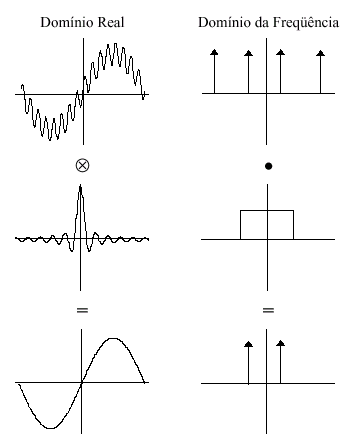
Figura 3-2 Comparação entre Filtragem no Domínio Real e no da Freqüência
Mas, surge um outro problema: estamos trabalhando com uma função
discretizada e com a DFT e não a FT. Como vimos a DFT é uma aproximação para a FT. Ao
aplicarmos algum tipo de filtragem com um filtro semelhante ao da Figura 3-2 (ideal), a
transformada inversa fornecerá uma imagem com um fenômeno chamado ringing (anelamento).
Visualmente este efeito é identificado por "anéis" (também chamados de
artefatos) que surgem nas bordas dos objetos da imagem. Este fenômeno acontece devido a
descontinuidade imposta pelo filtro ideal.
Para evitar a introdução de artefatos após a filtragem os filtros
devem ter sua borda suavizada por uma função com derivada contínua e faixa de
decaimento controlada. É muito comum o uso de uma gaussiana ou de um cosseno para tal. O
controle da faixa de decaimento permite o balanceamento entre a existência de artefatos e
o quanto o filtro permitirá passar outras freqüências que não aquelas sob o mesmo.
É preciso então saber balancear até que ponto a filtragem no
domínio real é vantajosa em relação ao domínio das freqüências. A convolução no
domínio real é definida como:
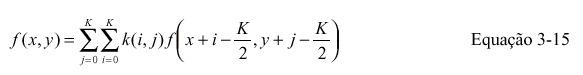
onde k é uma matriz quadrada de K 2 elementos.
Usando novamente o conceito de Complexidade Algorítmica, vemos que a
Equação 3-15 possui complexidade O(K 2 N 2 ). A filtragem no domínio da freqüência
exige um FFT, uma multiplicação pelo filtro e uma IFFT. Assim, a complexidade resultante
é O(N 2 xlogN) + O(N 2 ) + O(N 2 xlogN) = O(N 2 xlogN), ou seja comparável a
convolução no domínio real. É claro que o conceito de complexidade esconde diversas
constantes que se tornam relevantes na prática. Mas, de qualquer maneira isso mostra que
o tamanho da matriz de convolução K não pode ser muito grande.
Na prática K assume valores 3, 5, 7 e 9, e a filtragem no domínio da
freqüência permite uma seleção mais precisa de que elementos se deseja filtrar. Pois,
a filtragem espacial não deixa de ser uma média ponderada da vizinhança de um
determinado pixel, em contraste com uma visão global fornecida pela FT.
Como dito anteriormente, vários dos fenômenos ocorridos no domínio da freqüência são simples de serem modelados.
A filtragem mais básica de todas e também a mais conhecida é o filtro passa faixa. Quando este está próximo à origem é chamado de passa baixa. Quando está afastado é chamado de passa alta. No domínio bidimensional este filtro é representado por dois anéis concêntricos e centrados na origem, Figura 3-3.
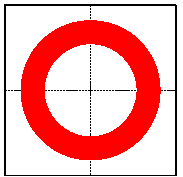
Figura 3-3 Setor Circular Centrado na Origem.
Dois casos particulares do filtro anterior acontecem quando queremos isolar apenas freqüências horizontais ou apenas verticais, como visto na Figura 3-4 e Figura 3-5, respectivamente.
Repare que para isolar freqüências horizontais necessitamos de um retângulo vertical, e vice-versa. Também pode-se ver dois retângulos simétricos em relação à origem, isto é necessário pois estamos supondo que a imagem complexa no domínio da freqüência proveio de uma imagem real no domínio espacial. Sendo assim, os filtros devem obedecer o fato das imagens complexas em questão serem hermitianas. Assim, quando calcularmos a transformada inversa obteremos uma imagem complexa com parte imaginária nula (próxima de zero), ou melhor, uma imagem real.(14v15h)

Figura 3-4 Retangular Vertical

Figura 3-5 Retangular Horizontal
Quando a imagem possui freqüências espaciais muito bem determinadas em ambas as direções estas freqüências se manifestam no domínio da freqüência através de pontos brilhantes, ou melhor, uma região brilhante ao redor de um ponto mais intenso, um pico. Para isolar estes picos necessitamos de um filtro que envolva os mesmos, o filtro da Figura 3-6 cumpre exatamente esse papel. Observe também sua característica hermitiana.

Figura 3-6 Oval Não Centrada na Origem
Estes picos comumente se manifestam de forma periódica. O filtro da Figura 3-7 simplifica o trabalho de repetirmos o filtro anterior para cada um dos picos presentes na imagem.

Figura 3-7 Oval Periódica
Algumas imagens podem ter freqüências distribuídas ao longo de uma direção inclinada. Estas freqüências aparecem com o formato de um setor angular como na Figura 3-8.
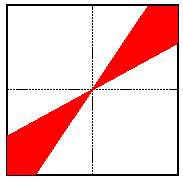
Figura 3-8 Setor Angular
Quando se deseja incluir toda informação próxima à origem, utiliza-se o filtro da Figura 3-9.
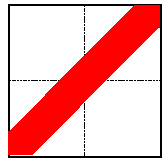
Figura 3-9 Retangular Inclinado Centrado na Origem
Portanto, vimos que os mais conhecidos fenômenos podem ser modelados por filtros simples de serem criados e manipulados, pois podem ser utilizados objetos geométricos bem conhecidos. Naturalmente, todos devem poder possuir uma borda suave durante a aplicação sobre a imagem. Matematicamente, a combinação de um ou mais filtros implica na união da área delimitada pelos mesmos. A área delimitada pela combinação dos filtros pode sobrepor a imagem durante a aplicação, atuando como um filtro que "passa" freqüências, ou o complemento desta área sobrepõe, atuando como um filtro que "rejeita" freqüências.
O método de filtragem com estes filtros é o mesmo descrito na Figura 3-2. A imagem original no domínio da freqüência é multiplicada pela imagem formada pelo uso de um ou mais filtros sobre a mesma.
A seqüência completa de filtragem pode ser vista na Figura 3-10. Deve-se aplicar a transformada de Fourier direta sobre a imagem que se deseja filtrar, criar e combinar os filtros que melhor isolem o fenômeno desejado, aplicá-los sobre a imagem complexa, calcular a transformada de Fourier inversa e por fim obtém-se a imagem original filtrada.
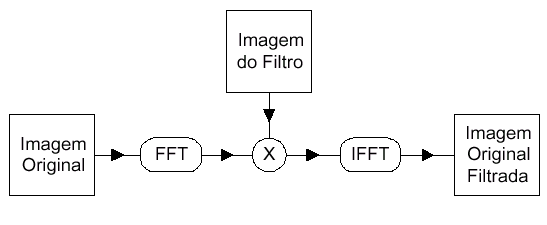
O filtros servem para suavisar ou realçar detalhes da imagem, ou ainda minimizar efeitos de ruído.
O sistema provê algumas máscaras pré-definidas para a aplicação de cada tipo de filtro. No caso da filtragem linear estão disponíveis máscaras para os filtros passa-baixa e passa-alta, descritos a seguir.
O efeito visual de um filtro passa-baixa é o de suavização da imagem e a redução do número de níveis de cinza da cena. As altas freqüências, que correspondem às transições abruptas são atenuadas. A suavização tende a minimizar ruídos e apresenta o efeito de borramento da imagem.
Algumas janelas que efetuam uma filtragem passa-baixa, numa vizinhança de dimensão 3x3, 5x5 ou 7x7 estão indicadas abaixo, estes filtros são conhecidos por filtros de média, pois obtém a média entre pontos vizinhos.
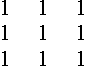 *1/9
*1/9 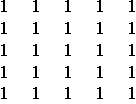 *1/25
*1/25
 *1/49
*1/49
Outros tipos de filtro passa-baixa, conhecidos como filtros de média ponderada, são usados quando os pesos são definidos em funcão de sua distância do peso central. Filtros desse tipo de dimensão 3x3 são:
 *1/10
*1/10  *1/16
*1/16
As figuras abaixo mostram duas cenas do satélite Landsat 5 (banda 5), onde a da esquerda é a imagem original realçada linearmente e da direita a mesma imagem, porém foi aplicado um filtro passa baixo de 7x7.


A filtragem passa-alta tende a realçar os detalhes, produzindo uma "agudização" (“sharpering”) da imagem, isto é, as transições entre regiões diferentes tornam-se mais nítidas. Exemplos: limites de um campo de cultivo, lineamento geológico, etc.
Estes filtros podem ser usados para realçar certas características presentes na imagem, tais como bordas, linhas curvas ou manchas. O efeito indesejado é o de enfatizar o ruído porventura existente na imagem.
No caso de filtragem passa-altas alguns exemplos podem ser dados, como:
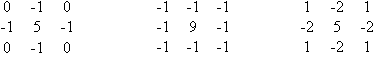
Os filtros de realce de bordas atribuem valores de nível de cinza para os "pixels" da cena original, segundo a influência de seus "pixels" vizinhos. Esta maior ou menor influência será função de valores (positivos, nulos ou negativos) fornecidos pelo usuário e atribuídos aos elementos da máscara, considerados segundo a configuração do filtro utilizado. É através da combinação destes valores de entrada ou pesos, que se obterá um realce maior ou menor da cena, segundo direções preferenciais de interesse.
As janelas abaixo são utilizadas para o realçamento de bordas em vários sentidos. O nome dado às máscaras indica a direção ortogonal preferencial em que será realçado o limite de borda. Assim, a máscara norte realça limites horizontais.
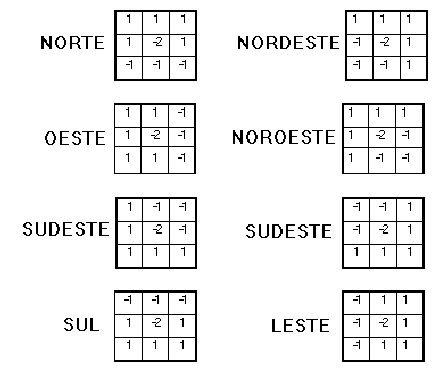 Exemplo de filtros direcionais.
Exemplo de filtros direcionais.
Realce não-direcional de bordas: é utilizado quando o usuário deseja realçar bordas, independentemente da direção.
O SPRING sugere três máscaras, que diferem quanto à intensidade de altos valores de níveis de cinza presentes na imagem resultante. Neste caso, as bordas podem ser realçadas com as seguintes intensidades:
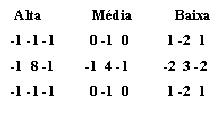
A máscara alta deixa passar menos os baixos níveis de cinza, isto é, a imagem fica mais clara. A máscara baixa produz uma imagem mais escura que a anterior. A máscara média apresenta resultados intermediários.
Realce de imagens: esta opção corresponde à utilização de máscaras apropriadas ao realce de características de imagens obtidas por sensor específico.
Atualmente, está disponível somente para imagens TM/Landsat. A máscara
utilizada neste caso é:
Este realce foi definido para compensar distorções radiométricas do sensor TM (trabalho
desenvolvido por Banon, em 1992). O "pixel" que terá seu valor de nível
de cinza substituído pela aplicação da máscara, corresponde à posição sombreada.
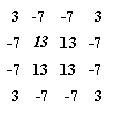
As figuras abaixo mostram duas cenas do satélite Landsat 5 (banda 5), onde a da esquerda é a imagem original realçada linearmente e da direita a mesma imagem, porém foi aplicado um filtro Realce de Imagem TM citado acima.


Além destas opções para filtragem linear com máscaras pré-definidas, existe também um Editor de máscaras para filtros lineares. Deste modo o usuário pode criar, atualizar, suprimir e aplicar suas próprias máscaras e visualizar máscaras pré-definidas para o sistema, que não podem ser modificadas.
As máscaras criadas devem ter dimensões m x n, onde m = 1, 3, 5 ou 7 e n = 1, 3, 5 ou 7, podem ou não ser normalizadas e aplicadas k vezes, onde k = 1, 2, ... 10.
Normalizar uma máscara significa que o valor resultante da aplicação da máscara será dividido pelo somatório dos pesos.
Por exemplo, em uma máscara 3x3, de valor 1, cada valor obtido da aplicação da máscara sobre a imagem será dividido por 9.
A normalização garante que as características estatísticas da imagem (como média), serão mantidas na imagem filtrada.
O usuário pode decidir se a máscara será ou não normalizada.
Utilizam-se filtros não-lineares para alterar a imagem, sem diminuir sua resolução. Servem para minimizar/realçar ruídos e suavizar/realçar bordas.
Na categoria de filtragem não-linear, estão disponíveis os filtros: operadores para detecção de bordas e filtros morfológicos. Seguem as descrições.
A detecção de características, tais como bordas, linhas, curvas e manchas, pode ser feita também com filtros não-lineares. No sistema estão disponíveis os operadores de Roberts e Sobel.
Operador de Roberts: o operador gradiente de Roberts é o método não-linear mais simples utilizado para detecção de bordas. Apresenta a desvantagem de dependendo da direção, certas bordas serem mais realçadas que outras, mesmo tendo magnitude igual.
Como resultado de sua aplicação, obtém-se uma imagem com altos valores de nível de cinza, em regiões de limites bem definidos e valores baixos em regiões de limites suaves, sendo 0 para regiões de nível de cinza constante.
O operador consiste na seguinte função:
(a') = (a - d)2 + (c - b)2
| a | b |
| c | d |
onde:
a' - é o nível de cinza correspondente à localização a, a ser substituído;
a, b, c, d - são as localizações cujos valores serão computados para a operação.
A figura a seguir ilustra o efeito de sua aplicação.

Operador de Sobel: o operador gradiente de Sobel tem a propriedade de realçar linhas verticais e horizontais mais escuras que o fundo, sem realçar pontos isolados.
Consiste na aplicação de duas máscaras, descritas a seguir, que compõem um resultado único:
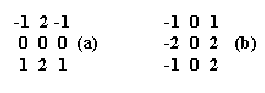
A máscara (a) detecta as variações no sentido horizontal e a máscara (b), no sentido vertical. O resultado desta aplicação, em cada "pixel", é dado por:

onde a' é o valor de nível de cinza correspondente à localização do elemento central da máscara.
A figura a seguir ilustra o efeito de sua aplicação.
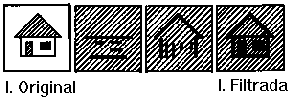
As figuras abaixo mostram duas cenas do satélite Landsat 5 (banda 5), onde a da esquerda é a imagem original realçada linearmente e da direita a mesma imagem, porém foi aplicado um filtro de realce de Sobel.


Exploram as propriedades geométricas dos sinais (níveis de cinza da imagem).
Para filtros morfológicos, as máscaras são denominadas elementos estruturantes. Estes elementos devem apresentar valores 0 ou 1, de modo a considerar ou não, o "pixel" correspondente à posição da matriz.
O SPRING fornece os seguintes filtros morfológicos: o filtro da mediana, erosão e dilatação.
Filtro morfológico da mediana: é utilizado para suavização e
eliminação de ruído. Mantém-se a dimensão da imagem. Exemplo: 
A posição sombreada será alterada para o valor 6, visto que é o valor mediano na ordenação [2,3,6,6,8].
Filtro morfológico de erosão: provoca efeitos de erosão das partes claras da imagem (altos níveis de cinza), gerando imagens mais escuras.
Considerando o exemplo anterior, o valor a ser substituído na posição sombreada corresponde ao menor valor da ordenação, no caso, 2. Filtro morfológico de dilatação: provoca efeitos de dilatação das partes escuras da imagem (baixos níveis de cinza), gerando imagens mais claras.
Para o exemplo anterior, o valor resultante da aplicação deste filtro é o maior valor na ordenação, no caso, 8.
Para a aplicação destes filtros, o sistema provê os seguintes elementos estruturantes pré-definidos:
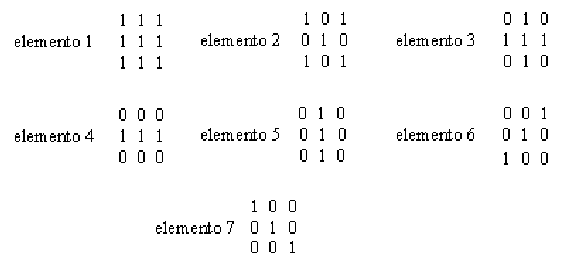 Exemplo de elementos estruturantes.
Exemplo de elementos estruturantes.
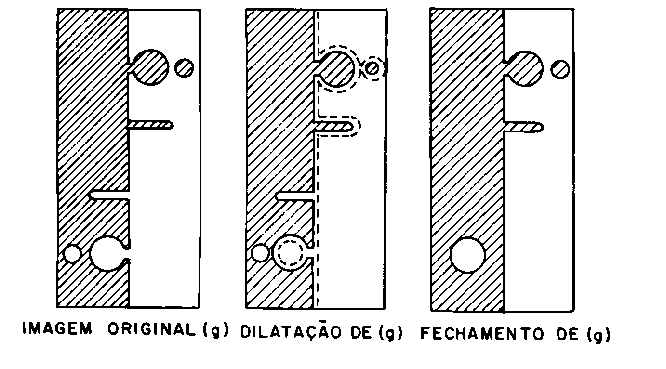
Abertura e fechamento de uma imagem: geralmente encadeiam-se filtros de erosão e dilatação com o mesmo elemento estruturante para obtenção de efeitos de abertura e fechamento.
A abertura é obtida pelo encadeamento do filtro de erosão, seguido pelo de dilatação, conforme ilustra a figura a seguir. No exemplo, há quebra de istmos e eliminação de cabos e ilhas.
 Exemplo de Erosão.
Exemplo de Erosão.
A figura original mostra a representação de uma imagem binária (valores de níveis de cinza 0 e 1). O efeito de fechamento é obtido pelo encadeamento do filtro de dilatação, seguido pelo de erosão. No exemplo, há eliminação de golfos e fechamento de baías.
 Exemplo de Dilatação.
Exemplo de Dilatação.
Existe também um Editor de elementos estruturantes para filtros morfológicos. Neste caso, os elementos estruturantes têm dimensão fixa 3x3, e seus elementos podem ser somente 0's ou 1's. No editor, os elementos estruturantes podem ser aplicados k vezes, onde k = 1, ..., 10.
Muitos filtros espaciais tem sido desenvolvidos para a redução do ruído Speckle e para o aumento da relação sinal-ruído, objetivando uma melhoria na separabilidade entre os alvos da superfície, com a mínima perda de informação.
Filtro de Frost [Frost-1982]: é um filtro convolucional linear, derivado da minimização do erro médio quadrático sobre o modelo multiplicativo do ruído. Neste filtro incorpora-se a dependência estatística do sinal original, uma vez que se supõe uma função de correlação espacial exponencial entre pixels. É um filtro adaptativo que preserva a estrutura de bordas.
Filtro de Lee [Lee-1981]: adota um modelo multiplicativo para o ruído e obedece o critério de "local linear minimum mean square error". Local, porque utiliza estatísticas locais do pixel a ser filtrado, admitindo a não estacionaridade da média e da variância do sinal. É um filtro linear porque realiza uma linearização por expansão em série de Taylor da multiplicação do sinal e o ruído em torno da média, utilizando apenas os termos lineares. O resultado da linearização transforma o modelo multiplicativo do ruído em aditivo, ou seja, o ruído e o sinal tornam-se independentes; e, finalmente, "minimum mean square error", porque minimiza o erro médio quadrático através do filtro de Wiener (filtro baseado no critério de mínimo erro médio quadrático). O filtro de Lee é um filtro adaptativo e geral.
Filtro de Kuan/Nathan [Kuan et al.-1982]: adota o modelo multiplicativo. O procedimento é semelhante àquele de Lee, onde a estimação ponto a ponto é feita utilizando-se o filtro de Wiener. A diferença entre eles, entretanto, consiste no fato de que no filtro de Kuan/Nathan não se realiza nenhuma aproximação. É também um filtro adaptativo e geral.
As figuras a seguir mostram a imagem original (ERS-1, 8 "looks") e as correspondentes imagens filtradas, utilizando os seguintes filtros: Filtro de média 5x5, Filtro de Frost adaptadivo, Filtro de mediana, Filtro de Lee fixo e Filtro de Kuan fixo (janela = 3).
 Original
Original  Média 3x3
Média 3x3
 Frost
Frost  Mediana
Mediana
 Lee
Lee  Kuan
Kuan
Medidas quantitativas realizadas nos filtros testados, mostraram que os filtros de Lee, Kuan, Frost e de Média preservam o valor médio da imagem. Os filtros não específicos para ruído Speckle, Média e Mediana, apresentam uma considerável redução no desvio padrão, implicando em uma grande perda de informação (perda de resolução). O filtro de Frost apresentou a máxima preservação de textura e uma menor perda de informação.
A utilização de um determinado filtro é dependente da aplicação desejada. Para uma determinada aplicação, se o fator mais importante for:
As figuras 5-1, 5-2 e 5-3 foram incluídas com o objetivo de demonstrar a corretude da FFT utilizada e de mostrar algumas propriedades da imagem obtida com a Transformada de Fourier. As figuras seguintes exemplificam a metodologia de filtragem usando alguns dos filtros propostos.
Um pulso bidimensional pode ser representado de várias maneiras. Apresentamos duas delas, a primeira com duração igual em todas as direções a partir da origem e a segunda com duração igual ao longo de cada eixo, ou seja, um círculo (Figura 16-1) e um quadrado (Figura 16-2), respectivamente. Sabemos que a FT de um pulso é uma função sinc 5 , como visto na Figura 3-2. Na FT da imagem com o círculo a sinc se manifestará em todas as direções. Já na FT da imagem com o quadrado, a sinc se manifestará apenas na direção vertical e na horizontal. No caso bidimensional estamos observando a função de um ponto de vista superior, como se a imagem estivesse no plano X-Y e estivéssemos sobre o eixo Z olhando para baixo.

Figura 16-1 FFT de um Círculo

Figura 16-2 FFT de um Quadrado
A Figura 16-3 mostra um grid e sua transformada. O grid pode ser interpretado como um trem de impulsos bidimensional, desconsiderando a linha contínua de freqüência zero. Sendo assim sua transformada é também um trem de impulsos (parte imaginária zero, uma função, ou melhor imagem real), mas com uma periodicidade diferente. É interessante observar que as linhas contínuas são de certa maneira consideradas ao observarmos que os valores da cruz central são maiores que os valores internos aos quadrantes.

Figura 16-3 FFT de um Grid

Figura 16-4 Filtragem de Baixas e Altas Freqüências
Utilizando um filtro passa baixa bidimensional, como visto na Figura 16-4, obtemos uma imagem "borrada", ou seja ocorre uma perda de detalhes que são compostos de altas freqüências. Aplicando o inverso deste filtro explicitamos os detalhes perdidos na imagem anterior.(25)

Figura 16-5 Eliminação da Cruz Central
Como visto na seção 4 Transformada de Fourier a transformada de uma imagem com bordas distintas gera a cruz central vista na Figura 16-5. Aplicando-se uma máscara na imagem original que elimina essa discontinuidade, obtemos uma imagem complexa da transformada sem a cruz central, o que permite uma melhor visualização dos fenômenos ocorridos no domínio da freqüência. Este procedimento é pouco usado pois é necessário uma interferência na imagem original muitas vezes não desejada.

Figura 16-6 Filtragem de um Ruído com Periodicidade Horizontal
Esta imagem foi capturada de um digitalizador de sinal de vídeo quando a imagem no vídeo não estava bem posicionada gerando um ruído horizontal com uma periodicidade bem definida. A escolha do filtro é feita percebendo-se esta periodicidade e aplicando um filtro retangular vertical (horizontal band pass). A imagem resultante da filtragem é vista sem o ruído em questão.

Figura 16-7 Filtragem de Linhas Diagonais em um Chip
A imagem do chip vista na figura possui inúmeras linhas diagonais em duas direções, que se manifestam no domínio da freqüência como o X visto na imagem da transformada. Cada um dos traços corresponde a um grupo de linhas diagonais. Isolando apenas um dos grupos e preservando o resto da imagem complexa, obtemos a imagem original sem aquele conjunto de linhas diagonais.
Esta filtragem pode ser usada para um detecção de bordas específica para linhas retas na imagem.

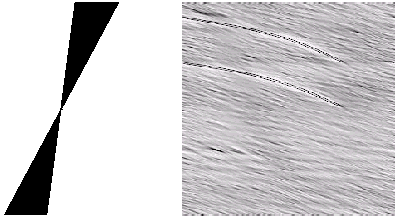
Figura 16-8 Filtragem de Curvas Sobre Grid Confuso.
A imagem inicial na seqüência da Figura 16-8 foi capturada através de um scanner e embora possua uma boa resolução a cópia original em papel não era bem definida gerando a imagem vista. O nosso interesse sobre esta imagem é isolar as duas classes de curvas que fornecem informações de cálculo, que uma vez no computador podem ser utilizadas por programas tornando o processo automático.
O grid, mesmo confuso, parece ter alguma propriedade periódica. Ao calcularmos a FT da imagem original observamos três manifestações distintas: linhas verticais que provavelmente provêem do grid, uma linha inclinada muito bem definida e uma região esparsa em um setor angular. Isolamos as duas últimas regiões e obtivemos o contorno das curvas desejadas.
A curva que possui transforma uma linha inclinada bem definida, observando-se melhor, é muito semelhante a uma reta inclinada (uma linha diagonal), que como vimos na Figura 16-7 pode ser isolada. Já a outra curva se manifesta como se existissem diversas linhas diagonais 6 que combinadas formam a curva, por isso a formação da região esparsa em um setor angular.
Referências Bibliográficas
| ALBUQUERQUE, M.P. de. Processamento de Imagens: Métodos e Análises. |
| FALCÃO, Alexandre Xavier & LEITE, Neucimar Jerônimo. Tópicos em Processamento de Imagens. UNICAMP. |
| Gonzales, Rafael & WOODSD, Richard. Digital Image Processing, Addison-Weslley Publishing Company, 1993. |
| PACIORNIK, Sidnei. Introdução ao Processamento Digital de Imagens. PUC-RIO. |
| PARKER, J.R. Algoritms for Image Processing and Computer Vision. Addison-Wesley Publishing Company, 1993. |
| RUSS, John C. The Image Processing Handbook. CRC Press, 1994 INPE. |
| ARGOUD, Fernada Isabel Marques. Detecção e Reconhecimento Automático de Atividades Epileptiformes no Encefalograma. Exame de Qualificação, UFSC, GPEB, Florianópolis, 1998.RUSS, John C. |
| BIRAN, Adrian and BREINER, Mosher. MATLAB for Engineers Addison -Wesley Publishing Company. 1995 . |
| IFEACHOR, Emmanuel C. and JERVIS, Barrier W. Digital Signal Processing. Addison- Wesley Publishing Company.1993. |
| KRAUSS, Thomas and SHURE Loren and LITTE, JOHN N. Signal Processing Toolbox for Use with MATLAB. Math Works Inc. |
| OPPENHEIM, Alan V. and SCHAFER Thomas and SHURE Loren and LITTLE, JOHN N. Signal Processing.Englewood Cliffs, New Jersey : Prentice-Hall. |
| SIQUEIRA, José Carlos Goulart E 703/803. Escola Federal de Engenharia de Itajubá. |
| E. O. BRigham " The Faust Fourier Transform" Englewood Cliffs, Prentice Hall, 1974. |
| M. A. O'Neill " Faster Than Fast Fourier " BYTE, Abril págs.293-300, 1988. |
| R. C. Gonzales & P. Wintz " Digital Image Processing" Addison Wesley, 1987. |
| K. R. Castlemanl " Digital Image Processing " Prentice_Hall, Inc., Englewood Cliffs, 1979. |
| www.ime.usp.br/~cesar |