Anisotropic Diffusion
Many of the results derived so far can be generalized to the case where
the conduction coefficient is not constant, but depends on spatial coordinates: 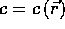 . This spatial variation leads to the so-called anisotropic diffusion
equation:
. This spatial variation leads to the so-called anisotropic diffusion
equation:

Note that this reduces to (2.1)
if c is constant. Two important points to note is that 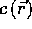 does not depend on time, and that we require that c is strictly
positive: c>0.
does not depend on time, and that we require that c is strictly
positive: c>0.

-
Proof
-
The proof closely parallels that of Theorem 6,
and basically requires some more careful arithmetic.
First, let 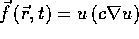 . Then
. Then 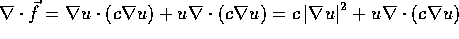 . On the other hand, the divergence theorem implies
. On the other hand, the divergence theorem implies 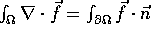 where
where 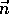 is the outward normal from the boundary
is the outward normal from the boundary 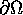 of the region
of the region 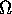 . Hence:
. Hence:
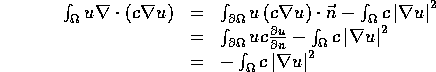
We apply the divergence theorem again to  :
:
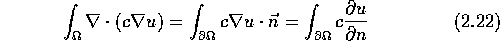
-
Let
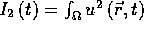 . Then:
. Then:
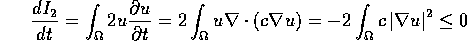
In particular, 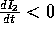 (strict), unless
(strict), unless 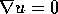 everywhere, which in turn requires u to be constant.
everywhere, which in turn requires u to be constant.
-
Suppose u attains its maximum value at some point in the interior
of
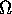 for some time
for some time 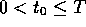 , say at
, say at 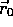 . Now, it may be that
. Now, it may be that 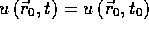 over some time interval
over some time interval 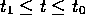 . Then there is a neighborhood of
. Then there is a neighborhood of 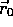 , say
, say 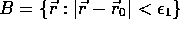 ,
, 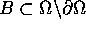 , and some time interval
, and some time interval 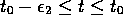 , in which both
, in which both 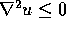 and
and 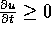 . But then the diffusion equation implies
. But then the diffusion equation implies 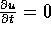 in this neighborhood. In particular,
in this neighborhood. In particular, 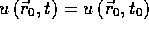 for some interval
for some interval 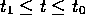 . Let
. Let 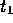 be the earliest time for which this holds.
be the earliest time for which this holds.
-
If
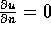 at all points on
at all points on 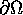 , then (2.22)
implies
, then (2.22)
implies 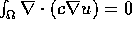 . Let
. Let 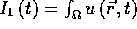 . Then:
. Then:
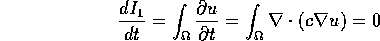
![]()
![]() does not depend on time, and that we require that c is strictly
positive: c>0.
does not depend on time, and that we require that c is strictly
positive: c>0.

![]() . Then
. Then ![]() . On the other hand, the divergence theorem implies
. On the other hand, the divergence theorem implies ![]() where
where ![]() is the outward normal from the boundary
is the outward normal from the boundary ![]() of the region
of the region ![]() . Hence:
. Hence:
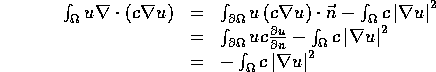
![]() :
:
![]()
![]() (strict), unless
(strict), unless ![]() everywhere, which in turn requires u to be constant.
everywhere, which in turn requires u to be constant.
![]()