 |
 |
|
|
|
Profº. Dr. Aldo von Wanghenhain
|
|
Nelson Abu Samra Rahal Junior
|
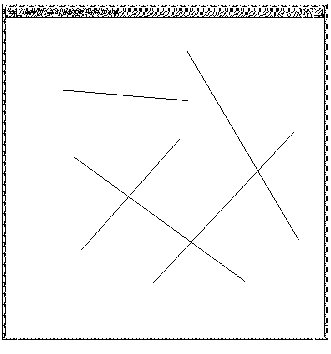
Através de mapeamento de elementos geométricos específicos, podemos identificar linhas retas, círculos, etc. em imagens computacionais.
Transformada de Hough é o método mais aceito para detecção de objetos. Ele utiliza a parametrização do objeto desejado para seu reconhecimento de linhas retas, circunferências e elipses.
Através de uma equação reconhecemos o ponto inicial e final de um segmento de linha,e através de um threshold aumentamos a intensidade do pixel e conseguimos a compensação necessária para fecharmos os buracos existentes.
p = xcos(ß) + ycos(ß)
 |
 |
 |
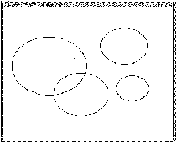 |
|
|
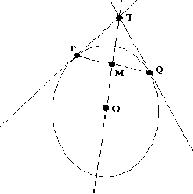
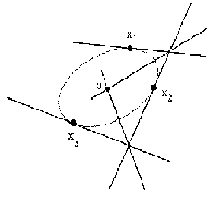
Elipse é definido pôr cinco parâmetros,onde consideramos dois pontos P e Q, e estimamos a tangente desses pontos .O ponto T é onde existe a intersecção da tangente , e o ponto M é central do ponto P e Q .Dividimos um elipse ao meio traçando uma reta do ponto T ao ponto M.
ax² + 2bxy + cy² = 1
 |
 |
6.Transformada probabilística de Hough
Somente para a proporção
X, onde (0% < X <= 100%). As escolhas dos pixels são randomicos.
Onde é definido em cima de uma imagem, uma função
de densidade uniforme (valor de X).
 |
 |
7.Transformada randômica de Hough
São escolhidos um par de pixel, e o parâmetro é uma única linha que passa através destes pixels, que são computados.
 |
 |
Usa uma técnica de estrutura de pirâmide, junto com uma grade de pequenas sub-imagens e aplica HT para detectar uma linha diretamente e executar cada uma delas.
 |
 |
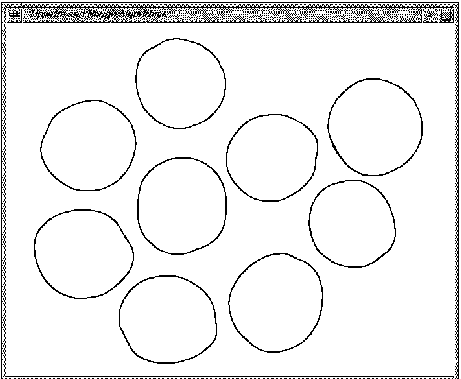
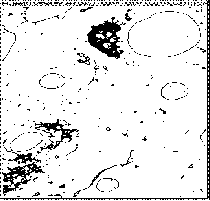
9.Hough Transformação
(Exemplos)
| Original | Padrão | Probabilistica | Randômica |
 |
 |
 |
 |
|
|
 |
 |
 |
 |
 |
|
||||
|
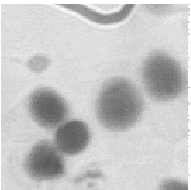
10.Hough Transformação
(Exemplos) Randômico
 |
 |
 |
 |
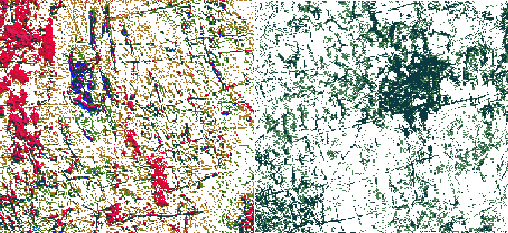 |
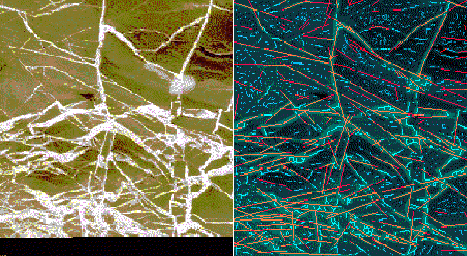
12.Alteração
do peak no threshold
35% - 40% - 45%
 |
 |
 |
 |
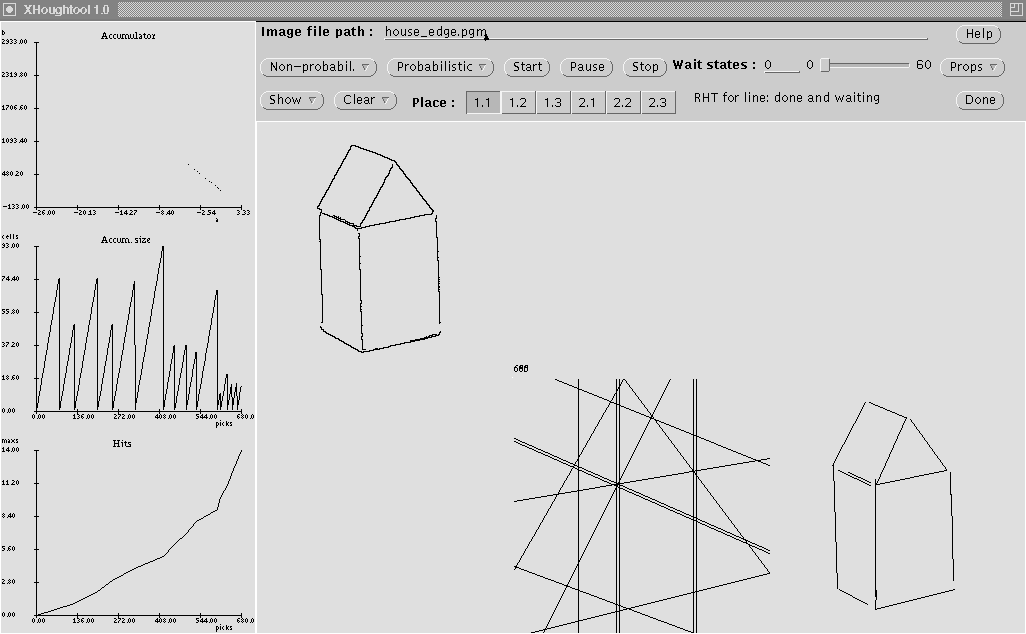
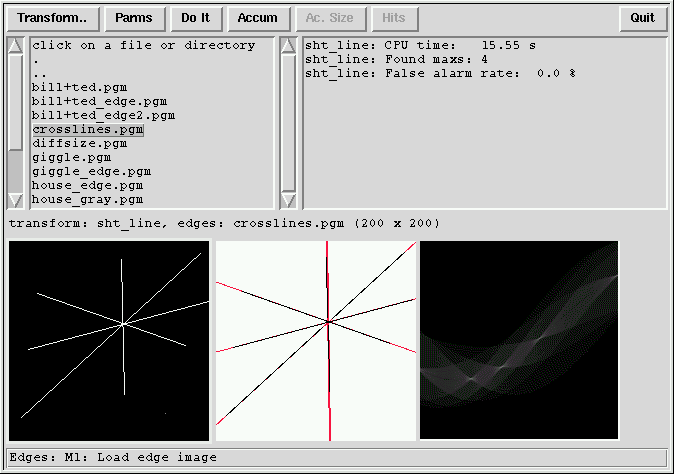
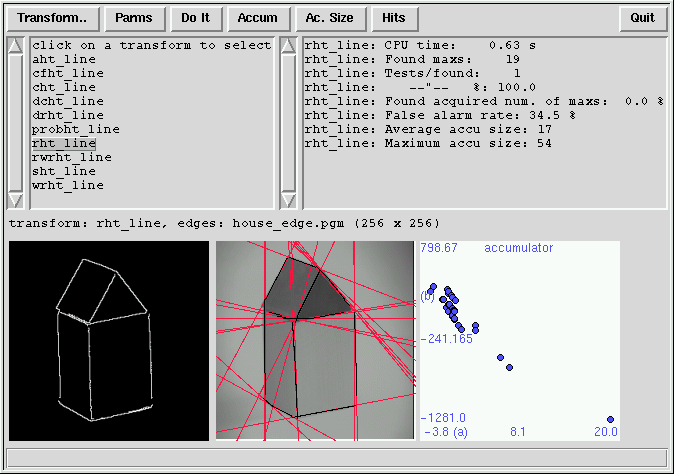
14.Software xhoughtool
O pacote de software Houghtool, tem como objetico realizar
a transformação de Hough.
São implementados vários métodos
de Hough Trasfomação para descoberta de linhas no pacote.
Estes incluem novas técnicas de Hough Trasfomação
como probabilistica aproximações, por exemplo o Randomized
Hough Transform (HT), que usa valores randomicos para a entrada de pontos.
Houghtool providencia ferramentas gerais para o desígnio de
algoritmos novos e prover soluções para aplicações
específicos. O design do software é flexível permitir
extensão do usuário das ferramentas provida. Com uma interface
de usuário, o XHoughtool, é prove uma visualização
do cálculo de Hough Tansform.
 |
 |
 |
 |
15.Algoritmo de Reconhecimento de Linhas
A transformação original de Hough só detecta porções com a descoberta de linhas diretas que usam a forma declive-intercepte. Para todo ponto de extremidade que é achado em uma imagem (x-y), o acumulador (m-b) é incrementado usando valores para o declive e y-intercepta essa satisfaça b = y - mx como indices:
A(m, b) = A(m, b) + 1
Cada ponto de extremidade tem uma
linha de parâmetro associada no acumulador. A interseção
de linhas de parâmetro indica a existência e posição
de pontos de collinear (Figura. 1). Quanto maior o número de pontos
de collinear, maior a sua probabilidade de se achar uma linha na imagem.
Esta técnica é estendida para descobrir outras curvas aumentando
o número de dimensões no acumulador do array.
Pontos de uma Imagem
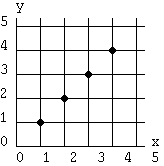 |
Linhas de Parametro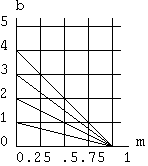 |
Acumulador de Celulas 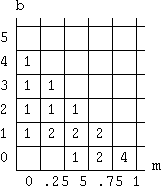 |
Figura 1 - Transformação de espaços de imagens para espaços de parametros
A eficiência computacional da transformado de Hough
fica aparente quando comparo com as exigências de uma técnica
exaustiva. Para cada n ponto da imagem, há (n - 1) collinear pontos
e (n - 1)/2 possíveis linhas que atravessam cada ponto. Comparando
as linhas que atravessam cada n(n de ponto - 1)) /2 para todo outro n(n(n
de ponto - 1)) /2 conduz para uma complexidade de n³.
Por outro lado, a complexidade do método de Hough
é dependente no número de incrementos requerido para o declive.
Para incrementos de k de m, a complexidade é só kn que é
muito mais baixo que n³ contanto que k não seja uma função
de, ou tão grande quanto n.
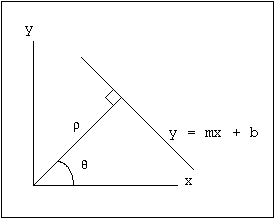
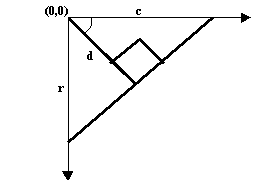
Figura 2 - (r,q) Representação de uma Linha
Da mesma maneira como a transformada original, para todo ponto encontrado de extremidade de uma imagem (x-y), o acumulador (q-r) é incrementado usando valores pelo ângulo e rádio que satisfazem r = xcos(q) + ysin(q) como indices:
A(q, r) = A(q, r) + 1
Esta " parameterização " de normal, produz
curvas de sinusoidal no acumulador. A interseção das curvas
indica as localizações prováveis de linhas na imagem
e o número encontrado de interseção indica o número
de pontos de linhas collinear. Considerando que a forma normal é
periódica, o alcance de valores para o ângulo é facilmente
limitado e as dificuldades encontraram com declives grandes no Hough original
é eliminado.
Enquanto o Hough transformam trabalha bem por achar tipos
específicos de curvas, a descoberta de formas arbitrárias,
requer uma generalização da técnica. Uma possível
solução seria tratar todas as curvas como coleções
de segmentos de linha pequenos. Cada segmento incrementaria A(q, r) com
um valor proporcional a sua duração. Os conteúdos
do acumulador poderiam ser comparados então com a característica
de arranjo de uma forma particular. Enquanto este método poderia
aparecer atraente, a presença de segmentos de linha estranhos em
uma imagem introduziriam um fator de ruído no acumulador que corromperia
o dados. Computações adicionais seriam necessárias
para filtrar o acumulador e extrair a pertinente informação.
INPUT
height: height of input image
width: width of input image
image: ARRAY[0 ... height-1
, 0 ... width-1] OF pixel
PARAMETER
NumTheta: INTEGER
// number of theta subintervals
DeltaRho: FLOATINGPOINT // The length
of a rho subinterval
DEFINE
sq(x) = x*x
sqrt(x) = square root of x
CONSTANT
PI = 3.1415927
VARIABLE
xc: INTEGER = trunc(width/2)
yc: INTEGER = trunc(height/2)
D: FLOAT = sqrt(sq(height)+sq(width))
HRho: INTEGER = ceil(D/(2*DeltaRho))
NumRho: INTEGER = 2*HRho+1
NumTheta: INTEGER = ceil(PI/2 * D/DeltaRho)
DeltaTheta: FLOATINGPOINT = pi/NumTheta
i, j, xx, yy: INTEGER
BEGIN
ALLOCATE A ARRAY[0 ... NumTheta-1, -HRho
... HRho] OF INTEGER
ALLOCATE C ARRAY[0 ... NumTheta-1] OF
FLOATING_POINT
ALLOCATE S ARRAY[0 ... NumTheta-1] OF
FLOATING_POINT
// Precompute tables of cosine and sine
FOR i FROM 0 TO NumTheta-1 DO
C[i] := cos(i*DeltaTheta)
/ DeltaRho
S[i] := sin(i*DeltaTheta)
/ DeltaRho
END
// Hough Transform
FOR each foreground pixel (x,y) DO
xx = x-xc; yy = y-yc
FOR i FROM 0 TO NumTheta-1
DO
Rho := xx*C[i]
+ yy*S[i]
j := round(Rho)
INC A[i,j] BY
1
END
END
FREE A, C, and S
END
/* 2D Hough transform by Mark Peters based on:
HT2D.C modified: 27 June, 1994 by Jesse Jin
Copyright Notice: see iplib.h | email jesse@cse.unsw.edu.au
I worked alone; no collaboration with any other students in the class.
recommended parameters:
line1.raw 128 128 5 4 256 180
line1.raw 128 128 8 2 256 180
line2.raw 128 128 16 2 256 180
line2.raw 128 128 18 2 256 180
================================================================================
*/
#include <stdio.h>
#include <stdlib.h>
#include <fcntl.h>
#include <malloc.h>
#include <math.h>
#include "iplib.h"
int *hough;
int *hough2;
u_char *uc;
u_char *oput;
u_char *image;
char *filename;
FILE *fd;
int iwidth, iheight, threshold, smooth, hwidth, hheight;
/*The values are supplied by the user as command line parameters, given
ih the order the are given here*/
int max;
int linevalue = 255;
/*Various values used for smoothing and locating peaks.*/
int top, left, bot, right, x, y, z, area, xavg, yavg;
int check, foundmore, peak, peakcount, movedir, lookdir, xoff, yoff;
/*These are values used as indiced to the image and the transform.*/
int across, down, row, col, smo;
/*These are values used to help create the correct values in the transform.*/
double diag, scale, theta;
main(argc, argv)
/*------------------- Load Image Data --------------------------------------*/
int argc;
char *argv[];
{
/*All these variables derive their values from the command line
input.*/
filename = argv[1];
iwidth = atoi(argv[2]);
iheight = atoi(argv[3]);
threshold = atoi(argv[4]);
smooth = atoi(argv[5]);
hwidth = atoi(argv[6]);
hheight = atoi(argv[7]);
if ((fd = fopen(filename, "r")) == NULL) OPENERR(filename);
uc = (u_char *)malloc(iwidth * iheight * sizeof(char));
if (uc == (u_char *)NULL) MEMERR();
fread(uc, sizeof(char), iwidth * iheight, fd);
fclose(fd);
image = (u_char *)malloc(iwidth * iheight * sizeof(char));
hough = (int *)calloc(hwidth * hheight, sizeof(int));
hough2 = (int *)calloc(hwidth * hheight, sizeof(int));
oput = (u_char *)malloc(hwidth * hheight * sizeof(char));
if (hough == (int *)NULL) MEMERR();
if (hough2 == (int *)NULL) MEMERR();
if (argc != 8)
{
printf("\nUsage: ImageFile ImageWidth ImageHeight
Threshold SmoothRange HoughWidth HoughHeight\n\n");
exit(0);
}
printf("\n\n Mark Peters 2141705 Hough Transform
1995.\n");
printf(" =========================================\n");
printf("\n Progress of program...\n\n");
printf("1 Loading complete\n");
/*-------------- Saving Original Image ------------------------------------*/
/*The program saves the data in a .pgm file so that more direct comparisons
of original data and reconstructed data are possible.*/
if ((fd = fopen("original.pgm", "w")) == NULL) OPENERR("original.pgm");
fprintf(fd, "P5\n%d %d\n255\n", iwidth, iheight);
fwrite(uc, sizeof(char), iwidth * iheight, fd);
fclose(fd);
printf(" Image saved in original.pgm\n");
free(uc);
/*------------------- Hough Transform --------------------------------------*/
/*Firstthe diagonal if the image is calculated for scaling all other
radii.*/
diag = sqrt((double)(iwidth * iwidth) + (double)(iheight * iheight));
/*Scaling to fit the given size of the hough array.*/
scale = hwidth / diag / 2;
max = 0;
for (down = 0; down < iheight; down++)
for (across = 0; across < iwidth; across++)
if (*(uc + down * iwidth + across) ==
linevalue)
{
for (row = 0; row < hheight;
row++)
{
/*The heart
of the transform.*/
theta = M_PI
* row / hheight;
col = (across
* cos(theta) + down * sin(theta) + diag) * scale;
if (++*(hough
+ row * hwidth + col) > max) max++;
}
}
printf("2 Transform complete\n");
/*------------------- Saving Hough Data ------------------------------------*/
if ((fd = fopen("hough.pgm", "w")) == NULL) OPENERR("hough.pgm");
for (row = 0; row < hheight; row++)
for (col = 0; col < hwidth; col++)
*(oput + row * hwidth + col) = *(hough
+ row * hwidth + col) * 255 / max;
fprintf(fd, "P5\n%d %d\n255\n", hwidth, hheight);
fwrite(oput, sizeof(char), hwidth * hheight, fd);
fclose(fd);
printf(" Highest peak = %d. Hough data
saved in hough.pgm\n", max);
free(oput);
/*------------------- Smoothing --------------------------------------------*/
/* The smoothing parameter describes the length of the side of the square
whose values are averaged. The area surrounding any particular location
varies as the location nears edges, this it taken into consideration.*/
max = 0;
smo = smooth / 2;
for (row = 0; row < hheight ; row++)
{
/*Finding the area that can be averaged.*/
if (row < smo) top = 0; else top = row - smo;
if (row > hheight - smo - 1) bot = hheight - 1;
else bot = row + smo;
for (col = 0; col < hwidth ; col++)
{
if (col < smo) left = 0; else left
= col - smo;
if (col > hwidth - smo - 1) right =
hwidth - 1; else right = col + smo;
area = (right - left + 1) * (bot - top
+ 1);
/* this is the value that accumulates
the surrounding cell total.*/
z = 0;
for (x = left; x < right + 1; x++)
for (y = top; y < bot
+ 1; y++)
z = z + *(hough
+ y * hwidth + x);
/*The smoothed value (average)
is copied into a new array, hough2,
to avoid contamination of
data in the original array, hough.*/
*(hough2 + row * hwidth
+ col) = z / area;
/*The maximum value is updated
to the point values can be scaled
to a 255 grey scale in the
image.*/
if (z / area > max) max
= z / area;
}
}
printf("3 Smoothing complete\n");
/*----------------- Saving Smoothed Data -----------------------------------*/
if ((fd = fopen("smooth.pgm", "w")) == NULL) OPENERR("smooth.pgm");
for (row = 0; row < hheight; row++)
for (col = 0; col < hwidth; col++)
*(oput + row * hwidth + col) = *(hough2
+ row * hwidth + col) * 255 / max;
fprintf(fd, "P5\n%d %d\n255\n", hwidth, hheight);
fwrite(oput, sizeof(char), hwidth * hheight, fd);
fclose(fd);
printf(" Highest peak = %d. Smoothed
data saved in smooth.pgm\n", max);
free(oput);
/*------------------- Thresholding -----------------------------------------*/
/*All values below the threshold are set to zero. This is primarily
for the
purposes of creating a file called threshold.pgm which reveals the
results of
thresholding.*/
for (row = 0; row < hheight; row++)
for (col = 0; col < hwidth; col++)
if (*(hough2 + row * hwidth + col) <
threshold)
*(hough2 + row * hwidth
+ col) = 0;
printf("4 Thresholding complete\n");
/*----------------- Saving Thresholded Data --------------------------------*/
if ((fd = fopen("threshold.pgm", "w")) == NULL) OPENERR("threshold.pgm");
for (row = 0; row < hheight; row++)
for (col = 0; col < hwidth; col++)
*(oput + row * hwidth + col) = *(hough2 + row *
hwidth + col) * 255 / max;
fprintf(fd, "P5\n%d %d\n255\n", hwidth, hheight);
fwrite(oput, sizeof(char), hwidth * hheight, fd);
fclose(fd);
printf(" Threshold = %d. Data saved
in threshold.pgm\n", threshold);
free(oput);
/*----------------- Averaging Peak Positions -------------------------------*/
/*Once the scanning process locates a peak the program the does a chain-code
like search to locate all the other points above the threshold which
are
connected. Once it has located all connected points it averages the
coord-
inates and records this location as the true peak. This technique was
used
so that the program would be discriminating of two linked peaks.*/
peakcount = 0;
for (row = 0; row < hheight; row++)
for (col = 0; col < hwidth; col++)
if(*(hough2 + row * hwidth + col) >
0)
{
area = 1;
movedir = 6;
x = col;
y = row;
xavg = 0;
yavg = 0;
peak = 1;
while (peak == 1)
{
*(hough2 + y
* hwidth + x) = 0;
xavg = xavg
+ x;
yavg = yavg
+ y;
/*The direction
of search is dependant on the inward direction of
movement.*/
if
(movedir == 0 | movedir == 1) {xoff = 1; yoff = 1;}
else if (movedir
== 2 | movedir == 3) {xoff = 1; yoff = -1;}
else if (movedir
== 4 | movedir == 5) {xoff = -1; yoff = -1;}
else if (movedir
== 6 | movedir == 7) {xoff = -1; yoff = 1;}
check = 0;
foundmore =
0;
while (check
< 7 && foundmore == 0)
{
check++;
if (*(hough2 + (y + yoff) * hwidth + x + xoff) > 0)
{
/*If the program finds a linked peak it moves to that
peak and continues the search process until it has
removed all peaks and collected their average loaction.*/
foundmore = 1;
area++;
x = x + xoff;
y = y + yoff;
if (xoff == 1 && yoff == 1)
{movedir = 7;}
else if (xoff == 1 && yoff == 0) {movedir = 0;}
else if (xoff == 1 && yoff == -1) {movedir = 1;}
else if (xoff == 0 && yoff == -1) {movedir = 2;}
else if (xoff == -1 && yoff == -1) {movedir = 3;}
else if (xoff == -1 && yoff == 0) {movedir = 4;}
else if (xoff == -1 && yoff == 1) {movedir = 5;}
else if (xoff == 0 && yoff == 1) {movedir = 6;}
}
else
{
/*If no linked peak is found the program moves its
attention to another point in a anti-clockwise way.*/
if (xoff == 1 && yoff == 1)
{yoff = 0;}
else if (xoff == 1 && yoff == 0) {yoff = -1;}
else if (xoff == 1 && yoff == -1) {xoff = 0;}
else if (xoff == 0 && yoff == -1) {xoff = -1;}
else if (xoff == -1 && yoff == -1) {yoff = 0;}
else if (xoff == -1 && yoff == 0) {yoff = 1;}
else if (xoff == -1 && yoff == 1) {xoff = 0;}
else if (xoff == 0 && yoff == 1) {xoff = 1;}
/*If the program comes through here 6 times it
breaks out of the loop, convinced that no more
connecting points exist.*/
}
}
if (foundmore
== 0)
{
/*Calculation and display of the actual true peak position.*/
xavg = xavg / area;
yavg = yavg / area;
*(hough2 + yavg * hwidth + xavg) = -1;
peakcount++;
printf(" peak %d at : %d, %d.\n", peakcount, xavg,
yavg);
peak = 0;
}
}
}
printf("5 Peak Location complete\n");
/*-------------- Saving Peak Positions -------------------------------------*/
if ((fd = fopen("peaks.pgm", "w")) == NULL) OPENERR("peaks.pgm");
for (row = 0; row < hheight; row++)
for (col = 0; col < hwidth; col++)
*(oput + row * hwidth + col) = *(hough2
+ row * hwidth + col) * -255;
fprintf(fd, "P5\n%d %d\n255\n", hwidth, hheight);
fwrite(oput, sizeof(char), hwidth * hheight, fd);
fclose(fd);
printf(" Peaks = %d. Peak data saved
in peaks.pgm\n", peakcount);
free(oput);
/*-------------- Inverse Hough Transform -----------------------------------*/
/*values in the image array are reset to zero prior to lines being
drawn.*/
for (down = 0; down < iheight; down++)
for (across = 0; across > iwidth; across++)
*(image + down * iwidth + across) =
0;
for (row = 0; row < hheight; row++)
{
theta = M_PI * row / hheight;
for (col = 0; col < hwidth; col++)
if(*(hough2 + row * hwidth + col) <
0)
for (down = 0; down <
iheight; down++)
{
across = (col
/ scale - down * sin(theta) - diag) / cos(theta);
*(image + down
* iwidth + across) = 1;
}
}
printf("6 Inverse Transform complete\n");
/*-------------- Saving Reconstructed Image --------------------------------*/
if ((fd = fopen("lines.pgm", "w")) == NULL) OPENERR("lines.pgm");
for (down = 0; down < iheight; down++)
for (across = 0; across
< iwidth; across++)
*(uc + down * iwidth + across) = *(image
+ down * iwidth + across) * 255;
fprintf(fd, "P5\n%d %d\n255\n", iwidth, iheight);
fwrite(uc, sizeof(char), iwidth * iheight, fd);
fclose(fd);
printf(" Line data saved in lines.pgm\n");
free(uc);
exit(0);
}
1.John Immerkær. Some Remarks
on the Straight Line Hough Transform. Pattern Recognition Letters, Vol.
19, No.12, p. 1133-1135, 1998.
2.Hough, P.V.C. Method and Means
for Recognizing Complex Patterns. U.S. Patent 3,069,654, Dec. 18, 1962.
3.Haralick, Robert M. Computer
and robot vision, Volume I, p.578-588.