Universidade Federal de Santa Catarina

A visão computacional envolve a identificação e classificação de objetos em uma imagem, desta forma a detecção de bordas é uma ferramenta essencial no processo de análise de imagens. Este trabalho tem como objetivo dar uma breve introdução sobre os conceitos que envolvem o processo de detecção de bordas. A importância de tal processo é devido ao fato de que ao se detectar uma borda podemos localizar todos os objetos de uma imagem definindo desta forma, propriedades como área, perímetro e forma.

2. DETECÇÃO DE IMAGENS

O primeiro passo na análise de imagens é a separação ou a segmentação dos objetos dentro da imagem. Algoritmos de segmentação permitem achar diferenças entre dois ou mais objetos. A segmentação é baseada em dois conceitos: similaridade e descontinuidade.

Na segmentação procura-se distinguir as partículas umas das outras e do fundo. Esta distinção permitirá ao programa interpretar pixels contíguos e agrupá-los em regiões. Não existe um modelo formal para a segmentação, o processo é essencialmente empírico e deverá se ajustar a diferentes tipos de imagem. Esta etapa é a mais difícil do processo e também a mais delicada porque todas as medidas serão realizadas sobre as regiões identificadas nesta etapa. A segmentação é tão complexa porque tenta traduzir para o computador um processo cognitivo extremamente sofisticado realizado através da visão humana.

A descontinuidade em uma imagem pode ser:

um ponto isolado;
uma linha;
a borda de uma objeto.

2.1 ALGORITMOS DE SEGMENTAÇÃO

a) Detecção de pontos: é a mais simples técnica de detecção. Um ponto terá uma mudança drástica do valor de cinza em relação aos seus vizinhos.

b) Detecção de linhas: é o processo mais complicado, pois é necessário achar os pixels que são semelhantes e testá-los para verificar se são parte de uma linha comum.

c) Detecção de bordas: é uma das técnicas básicas utilizadas pela visão humana no reconhecimento de objetos. É o processo de localização e realce dos pixels de borda, aumentado o contraste entre a borda e o fundo. Este processo verifica a variação dos valores de luminosidade de uma imagem. Como foi abordado anteriormente, neste trabalho daremos ênfase apenas para os algoritmos de segmentação para detecção de bordas.

3. O QUE É UMA BORDA?

É o contorno entre um objeto e o fundo indicando o limite entre objetos sobrepostos Um CONTORNO é uma linha fechada formada pelas bordas de um objeto. Mas como conceituamos e detectamos uma borda computacionalmente?

Variações de intensidade complexas que ocorrem em uma região são geralmente chamadas de textura. Bordas são definidas como picos da magnitude do gradiente, ou seja, são variações abruptas que ocorrem ao longo de curvas baseadas nos valores do gradiente da imagem. As bordas são regiões da imagem onde ocorre uma mudança de intensidade em um certo intervalo do espaço, em uma certa direção. Isto corresponde a regiões de alta derivada espacial, que contém alta frequência espacial.

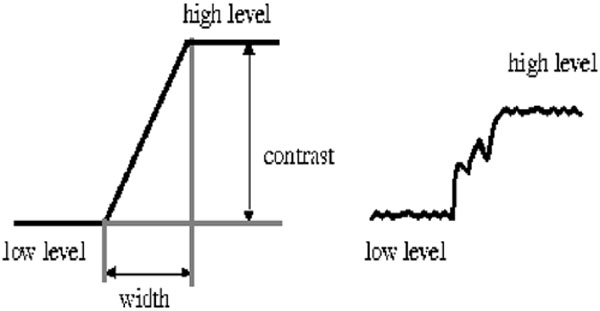
Borda unidimensional : pode ser definida como uma mudança de uma intensidade baixa para alta. A intensidade do sinal pode ser interferida por ruídos.

borda unidimensional

Figura 3.1: Gráfico da intensidade de uma imagem.

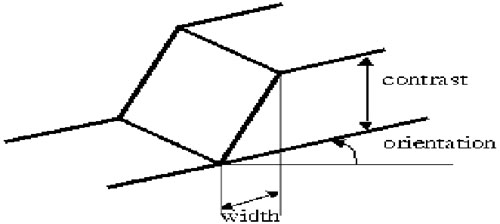
Borda bidimensional: as descontinuidades ocorrem ao longo de certas linhas ou orientações A orientação é uma característica importante em bordas 2-D

Figura 3.2: Gráfico da intensidade representando uma borda bidimensional.

3.1 Ruídos

A aquisição da imagem está sujeita a algum tipo de ruído, a situação ideal (sem ruído), na prática não existe. Ruídos não podem ser previstos pois são de natureza randômica e não podem nem mesmo ser medidos precisamente. Porém, algumas vezes ele pode ser caracterizado pelo efeito na imagem, e é geralmente expresso como uma distribuição de probabilidade com uma média específica e um desvio padrão. Existem dois tipos de ruídos específicos:

Ruído independente do sinal: é um conjunto randômico de níveis de cinza, estatisticamente independente dos dados da imagem. Este tipo de ruído acontece quando a imagem é transmitida eletronicamente de um lugar para outro.
- A - imagem perfeita
- N - é o ruído
- B - imagem final
- B= A+N

Ruído de sinal dependente: o nível do valor de ruído a cada ponto na imagem é uma função do nível de cinza.

4. Operadores para detecção de bordas - Operadores de derivadas

Desde que uma borda é definida por uma mudança no nível de cinza, quando ocorre uma denscontinuidade na intensidade, ou quando o grandiente da imagem tem uma variação abrupta, um operador que é sensível a estas mudanças operará como um detector de bordas.

Um operador de derivada faz exatamente esta função. Uma interpretação de uma derivada seria a taxa de mudança de uma função, e a taxa de mudança dos níveis de cinza em uma imagem é maior perto das bordas e menor em áreas constantes. Se pegarmos os valores da intensidade da imagem e acharmos os pontos onde a derivada é um ponto de máximo, nós teremos marcado suas bordas. Dado que as imagens são em duas dimensões, é importante considerar mudanças nos níveis de cinza em muitas direções. Por esta razão, derivadas parciais das imagens são usadas, com as respectivas direções X e Y. Uma estimativa da direção atual da borda pode ser obtida usando as derivadas x e y como os componentes da direção ao longo dos eixos, e computar o vetor soma. O operador envolvido é o gradiente, e se a imagem é vista como uma função de duas variáveis A(x,y) então o gradiente é definido como:

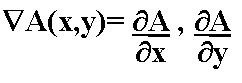
4.1 Mácaras dos Algoritmos de Segmentação

A maioria dos algoritmos de segmentação utilizam uma máscara sobre os pixels da imagem para detecção de uma descontinuidade. Cada pixel e seus pixels vizinhos tem um valor do nível de cinza multiplicados por uma constante. A soma destes valores representa a máscara de resposta daquele ponto.

Exemplo de uma máscara de resposta

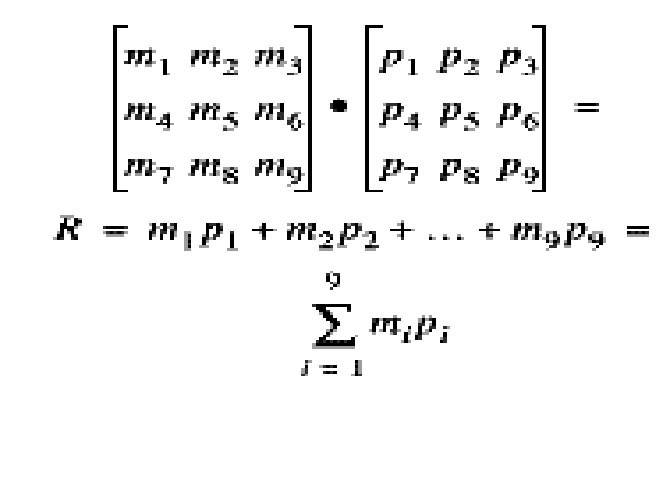
Onde:

mi: é valor para um pixel

pi: é o valor do nível de cinza para um pixe

R: é a máscara de resposta para o pixel central (p5).

Ampliando esta máscara atravessando a imagem linha por linha, um novo vetor é criado. É o mesmo que a imagem original mais contém os valores da máscara de resposta ao invés do valor do pixel. Estes valores da máscara de resposta podem então ser comparados com o valor mínimo de threshold para determinar quais pixels são mais prováveis de ser parte de uma borda. Este threshold pode ser ajustado para variar seletivamente de acordo com os pixels de borda, permitindo um usuário conduzir o algoritmo para um melhor desempenho para uma imagem específica.

Considerando o exemplo da máscara de entrada anterior e supondo um valor de threshold 20. A matriz 3x3 representa uma parte de uma determinada imagem, desde que os valores de saída que cancelem o valor central, não ultrapassem o valor de threshold, o que significa que a imagem não apresenta descontinuidade.

EXEMPLO1:

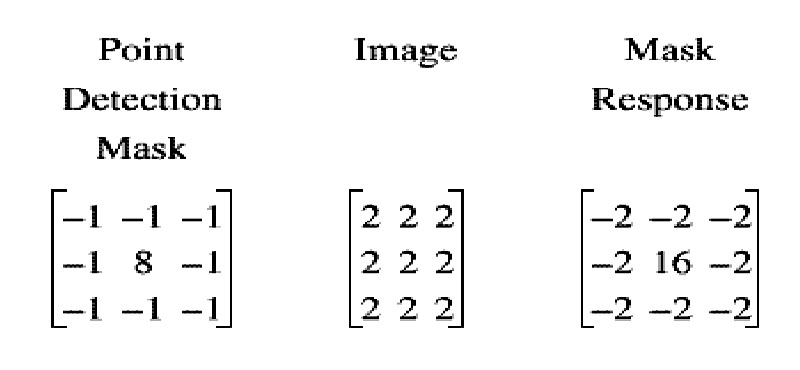
Analisando a máscara de resposta para o conjunto contínuo de pixels dados no exemplo acima, percebemos que neste caso o valor central da máscara é 16, e a soma de todos os pixels subtraída do valor central fornece zero como resposta. Como zero é um valor menor do que o threshold (20), o pixel central na imagem não é um ponto de descontinuidade.

EXEMPLO2:

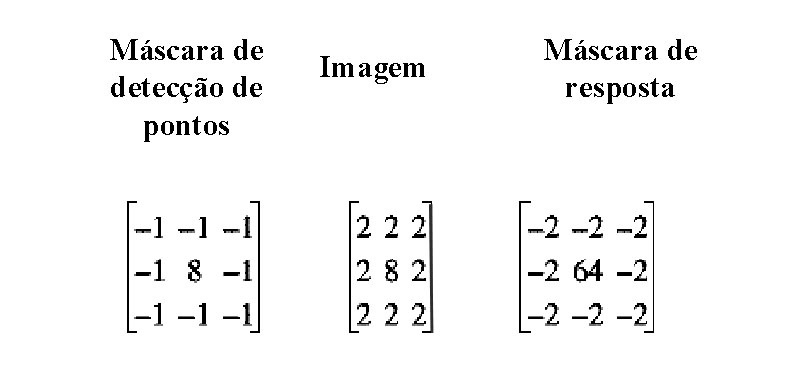
Neste caso o valor central da máscara é 64, a soma de todos os pixels subtraída do valor central fornece um valor de 48 que é maior do 20 (threshold), o pixel central na imagem é um ponto de descontinuidade, portanto seria um pixel de borda.

5. ALGORTMOS DE DETECÇÃO DE BORDAS

Os algoritmos para detecção de bordas que serão estudados no presente trabalho são:

Roberts
Sobel
Robison
Canny
Marr-Hildreth

5.1 Operador de Roberts

É o mais antigo e simples algoritmos de detecção de bordas. Utiliza uma matriz 2x2 para encontrar as mudanças nas direções x e y.

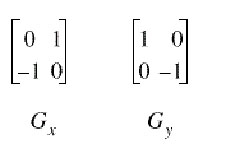
Figura 5.1.1: Máscara de Roberts.

Para determinar onde o pixel avaliado é ou não um pixel de borda, o gradiente é calculado da seguinte forma:

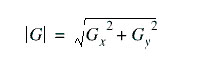
Figura 5.1.2: Fórmula para cálculo do gradiente

Se a magnitude calculada é maior do que o menor valor de entrada (definido de acordo com a natureza e qualidade da imagem que esta sendo processada), o pixel é considerado ser parte de um borda. A direção do gradiente da borda, perpendicular a direção da borda, é encontrada com a seguinte fórmula:

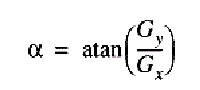
Figura 5.1.3: Fórmula para cálculo da magnitude

O pequeno tamanho da máscara para o operador de Roberts torna o mesmo fácil de se implementar e rápido para calcular a máscara de resposta. As respostas são muito sensíveis ao ruído na imagem.

5.2 Operador de Sobel

Utiliza duas máscaras para encontrar os gradientes vertical e horizontal das bordas.

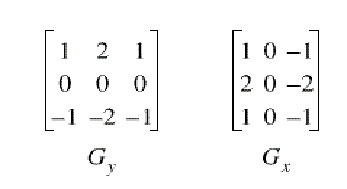
Figura 5.2.1: Máscaras de Sobel.

Considerações sobre o operador de Sobel

A fórmula para encontrar o gradiente e o ângulo são as mesmas do operador de Roberts.
O ângulo do gradiente corresponde direção de máxima variação da intensidade
Devido as máscaras serem 3X3 ao invés de 2X2, Sobel é muito menos sensível ao ruído do que Roberts.
Os resultados são mais precisos.
A computação de |G| se torna mais complexa. Na prática |G| é aproximada da seguinte forma: |G|= |Gx| + |Gy|.
O módulo do gradiente é proporcional a derivada local da intensidade.

5.3 Operador de Robinson

É similar em operação ao de Sobel, porém usa um conjunto de oito máscaras, onde quatro delas são as seguintes:

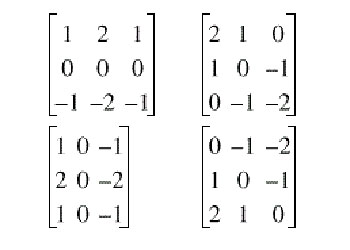
Figura 5.3.1: Máscaras de Robinson

As outras quatro são simplesmente negações destas quatro.A magnitude do gradiente é o valor máximo obtido ao aplicar todas as oito máscaras ao pixel vizinho, e o ângulo do gradiente pode ser aproximado como o ângulo na linha de zeros na máscara dando a resposta máxima. Este algoritmo aumenta a precisão de |G|, mas requer mais computação do que Roberts e Sobel, devido ao tamanho das máscaras.

5.4 Detector de bordas de Canny

Definiu um conjunto de metas que um detector de bordas deveria Ter são eles:

Taxa de erro: o detector de bordas deveria detectar e achar somente bordas, nenhuma borda deveria faltar;
Localização: a distância entre os pixels de borda encontradas pelo detector de bordas e a borda atual deveriam ser o menor possível;
Resposta: o detector de bordas não deveria identificar múltiplos pixels de borda onde somente exista um único pixel.

O detector de bordas de Canny é um filtro de convolução f que uniformizaria o ruído e localizaria as bordas. O problema é identificar um filtro que otimize os três critérios do detector de bordas. Se considerarmos uma borda de uma dimensão variando no contraste e então convolucionando a borda com a função de uniformização de Gauss, o resultado será uma variação contínua do valor inicial ao final, com uma inclinação máxima no ponto onde existe um "degrau". Se esta continuidade é diferenciada em relação a x, esta inclinação máxima será o máximo da nova função em relação a original. .

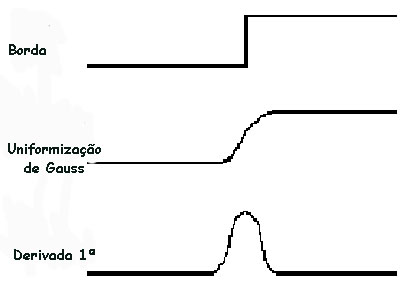
Figura 5.4.1: Detcção de bordas por Canny

Os máximos da convolução da máscara e da imagem indicarão bordas na imagem. Este processo pode ser realizado através do uso de uma função de Gauss de 2-Dimensões na direção de x e y. Os valores das máscaras de Gauss dependem da escolha do sigma na equação:

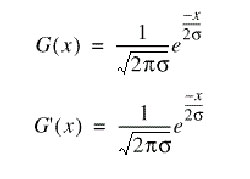
Figura 5.4.2: Função de Gauss

A aproximação do filtro de Canny para detecção de bordas é G'. Convolucionando a imagem com G' obtemos uma imagem I que mostrará as bordas, mesmo na presença de ruído. A convolução é relativamente simples de ser implementada, mas é cara computacionalmente, especialmente se for em 2-dimensões. Entretanto,uma convolução de Gauss de 2-dimensões pode ser separada em duas convoluções de Gauss de 1-dimensão.

A intensidade computacional do detector de bordas de Canny é relativamente alta, e os resultados são geralmente pós-processados para maior clareza. Entretanto, o algoritmo é mais eficiente no processamento de imagens com ruídos ou com bordas difusas.

Algoritmo de Canny

Ler a imagem I a ser processada;
Criar uma máscara de Gauss de 1-D G para convolucionar I. O desvio S de Gauss é um parâmetro para o detector de bordas;
Criar uma máscara de 1-D para a primeira derivada de Gauss nas direções x e y; nomear como Gx e Gy. O mesmo valor S é usado;
Convolucionar a imagem I com G percorrendo as linhas na direção x (Ix) e percorrer as colunas na direção y (Iy);
Convolucionar Ix, com Gx, para dar I´x, o componente x e de I convolucionado com a derivada de Gauss, e convolucionar Iy, com Gy para dar I´y;
Se você deseja ver o resultado neste ponto os componentes x e y devem ser " combinados". A magnitude do resultado é computada para cada pixel (x,y).

5.5 Operador de Marr-Hildreth

Um máximo da derivada primeira ocorrerá a cada zero crossing da derivada Segunda. Para localizar bordas horizontais e verticais procuramos a derivada Segunda nas direções de x e y. Isto é Laplacian de I:

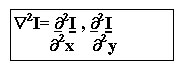
Laplacian é linear e simétrico rotacionalmente. Podemos procuar pelos zeros crossings da imagem primeiro uniformizando com uma máscara de Gauss e então calculando a derivada Segunda. Isto define o operador de Marr-Hildreth.

Figura 5.5.1: Zero Crossing

O operador de Marr-Hildreth tornou-se largamente utilizado devido:

a reputação de Marr;
pesquisadores encontraram campos nos olhos de animais que se comportavam de forma semelhante com este operador;
o operador é simétrico. Bordas são encontradas em todas as direções, diferente dos operadores que usam a primeira derivada (são unidirecionais).

Considerações sobre os operadores de derivadas de segunda ordem

Zero crossing da derivada segunda são mais simples de determinar do que o ponto de máximo em uma derivada de primeira ordem;
Zero crossing sempre formam contornos fechados. Isto é bom quando estamos tentando separar objetos em uma imagem.
No operador da Segunda derivada o ruído é considerado. Este método é muitas vezes usado em conjunção com limiarização normal para reduzir sua sensibilidade a ruído;
Gerar sempre contornos fechados não realista;
Marca bordas em algumas localizações que não são bordas.

Método de Marr-Hildreth

Borra-se a imagem com um kernel gaussiano;
Obtém-se o Laplacian;
Localiza-se os cruzamentos por zero;
Os pontos localizados formam contornos fechados.

6. LINKS RELACIONADOS