Visão Computacional
1998

Quadtrees e Octrees

Autor : Harley

 1. Quadtree

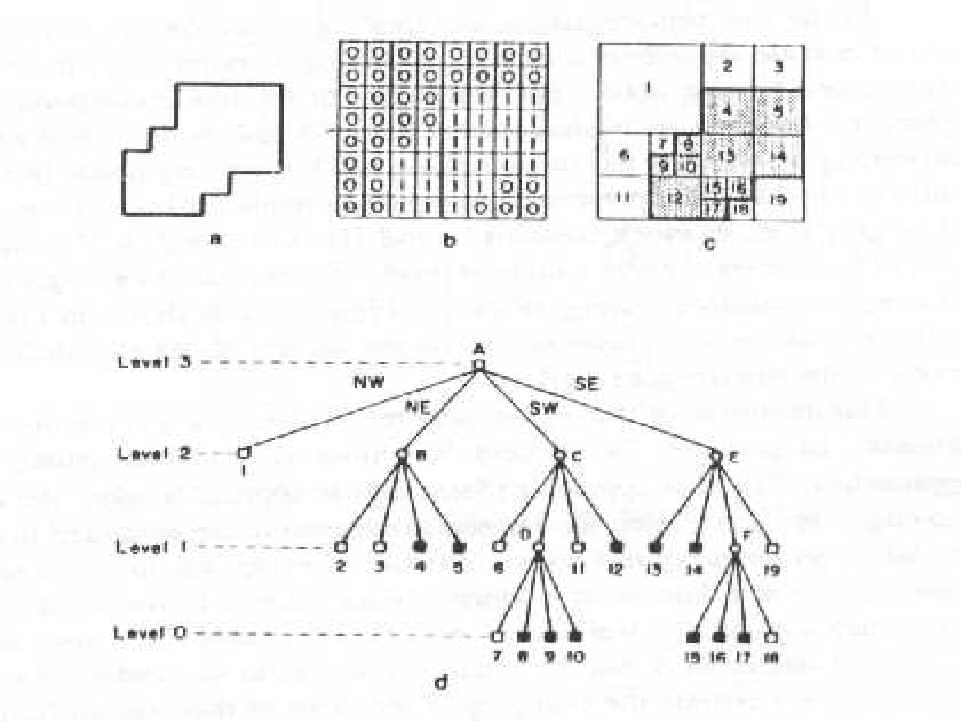
Há numerosas técnicas de estruturas de dados hierárquicos usados para representar dados de espaço. Uma técnica comumente usada é o quadtree. Seu desenvolvimento foi motivado por grande parte por uma necessidade de economizar armazenamento agregando dados que têm valores idênticos ou semelhantes. Quando se refere a quadtree, o contexto de regiões bi-dimensionais é trabalhado. Quando o assunto é região tridimensionais, o conceito é octree.

Assumindo a existência de uma ordem de elementos de uma figura (termos de pixels) em duas dimensões. Se seus elementos são pretos ou brancos, então é dito que é binário. Sendo tons de cinza (níveis cinzas), é dito que a imagem é uma escala de imagem cinza .

O termo quadtree é usado para descrever uma classe hierárquicos de estrutura de dados.

Na árvore de representação, o nodo raiz corresponde à ordem inteira. Cada filho de um nodo representa um quadante NW (nordeste), NE (noroeste), SW (sudoeste), SE (sudeste) da região representada por aquele nodo.

Os nodos de folha da árvore correspondem a blocos para os quais nenhuma subdivisão adicional é necessária.

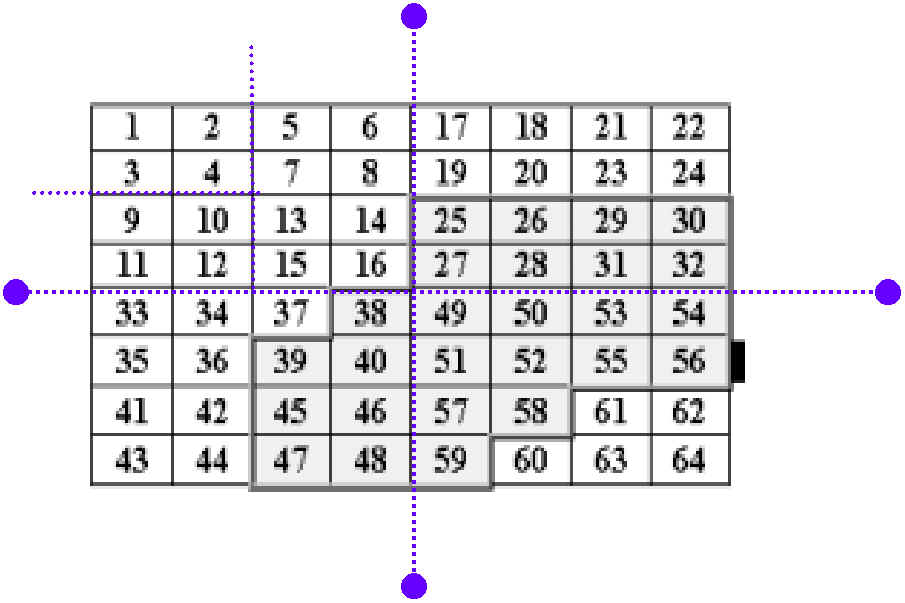
2. Ordem de Morton

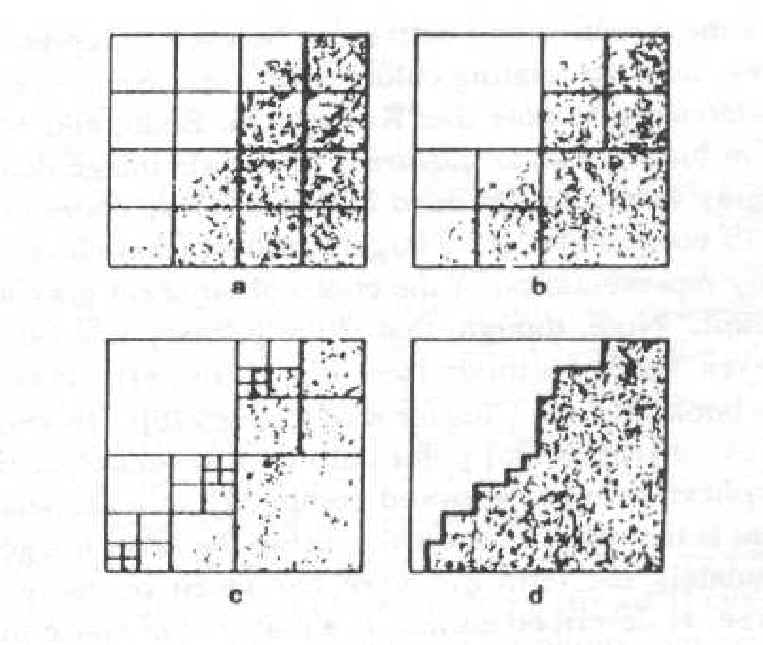
3. Exemplo de "divisão e fusão"

3. Octree

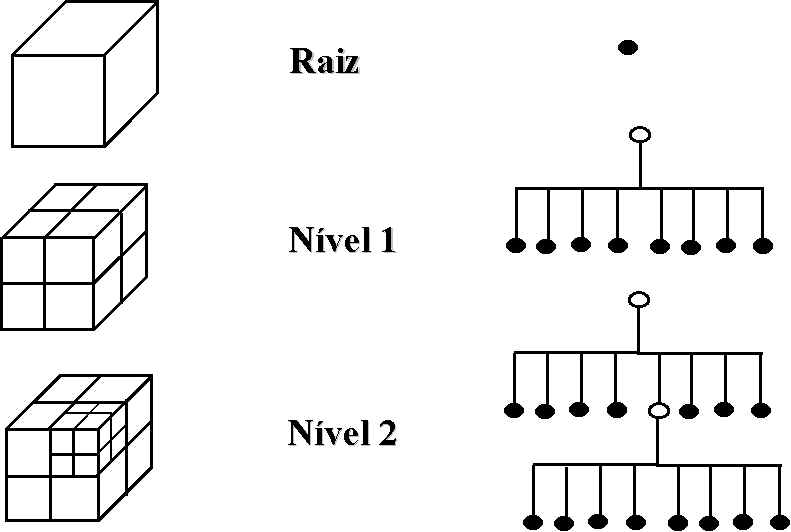
A quadtree é estendido para representar dados binários de região tridimensionais, a estrutura de dados resultante é chamada de OCTREE.

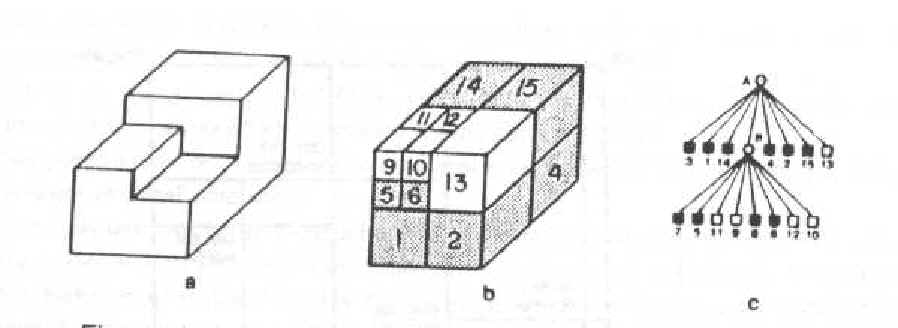
O processo de subdivisão é representado por uma árvore (8 filhos) no qual o nodo raiz representa o objeto inteiro e os nodos de folha correspondem a cubos de qual nenhuma subdivisão adicional é necessária.

Uma octree é uma estrutura de árvore de dados baseada em uma célula com oito "crianças". Cada célula de uma octree representa um cubo em espaço físico. Cada criança representa uma "octant" de seu pai. Nas folhas da árvore estão as células da grade computacional, estas células são classificadas como cartesianas ou corte.

3.1 Estrutura de dados octree

Pseudo-código para refinamento OCTREE

• • • refine (cell)

      compute (with a polygon clipper) input body clipped by cell.

      if input body is there

      • • and the curvature is above some threshold

          and level < maximum level then

        allocate space for cell’s eight children

        • • • refine (each child).

        else

        if input body remains then

        • compute cut-cell.

          • • else

            mark cell Cartesian.

            end if

end if

3.2 Octrees

As octrees são criadas de uma única célula raiz que cerca inteira o domínio de espaço do problema. A partir desta única célula, o algoritmo de refinamento recursivo constrói o restante da árvore como for necessário.

Simplesmente por, o cortador de polígono, retorna uma caixa (cubo), se há qualquer geometria dentro da célula, e a curvatura do corpo cortado é significante, o refinamento é permitido, então a célula é dividida em oito crianças, cada uma é recursivamente refinada.

Caso contrário, se há parte do corpo permanece dentro da célula, a célula será cortada, e a definição completa de célula cortada deve ser construída; se nenhuma geometria do corpo cortado está dentro da célula, então a célula é simplesmente marcada como Cartesiano.