Representação de Objetos

Processamento de imagem significa extração de informação da imagem. Imagem processada é a ciência da reestruturação. Podem ser alterados valores de pixel de acordo com o brilho do pixel vizinho, ou trocar para outro lugar na ordem deformando a imagem, mas a quantidade de pixels fica inalterada.

Medidas que podem ser executadas sobre características de imagem, pode-se agrupar em quatro classes: brilho, localização, tamanho e forma. Para cada classe, pode ser feita uma real variedade de medidas específicas e diferentes, e há variedade de modos diferentes para executar as operações. A maioria dos sistemas de análise de imagem oferecem pelo menos algumas medidas em cada classe.

Usuários se acham em algum momento em casa o outro lugar tendo que lidar com vários parâmetros de medida diferentes. Como nota-se, a maioria destas técnicas produz uma grande quantidade numérica para análise estatística ou gráficos de apresentação. Freqüentemente, a interpretação dos dados permanece a um programa separado, ou uma planilha eletrônica simples que confia na habilidade no usuário que está programando, ou um pacote de estatísticas dedicado. Em alguns casos, os números são convertidos para nenhuma decisão.

Exemplos poderiam incluir controle de qualidade que testa o tamanho e colocação de buracos em uma estrada, ou decisões de patologia médicas baseados na identificação da presença de células cancerosas. Depois que uma imagem for segmentada em regiões através de métodos discutidos na segmentação de imagens, o agregado resultante de pixels segmentado normalmente é representado e descrito em uma forma satisfatório para facilitar o processo computacional. Basicamente, representar uma região envolve duas escolhas:

Geralmente, uma representação externa é escolhida quando o enfoque primário está em características de forma. Uma representação interna é selecionada quando o enfoque primário está em propriedades de sua reflexibilidade, como cor e textura.

Nas imagens, cada pixel registra um valor numérico que é o brilho do ponto correspondente na cena original. Alguns valores podem ser combinados para representar informações de cor. O alcance típico dos valores de brilho é de 0 a 255 (8 bits), dependendo do aparelho de 0 a 65535 (16 bits). Muitas câmeras e outros dispositivos usados para adquirir imagens não são perfeitamente lineares (ou logaritmo) nem completamente consistente em relação entre o valor numérico do pixel e a entrada do sinal

Escolher um esquema de representação, porém, é só uma parte da tarefa de marcar os dados úteis para o computador. A próxima tarefa é descrever a região baseada na representação escolhida. Por exemplo, uma região pode ser representada por seu limite com o limite descrito por características como seu comprimento, a orientação da linha direta que une os pontos extremos, e o número de concavidades no limite.

As técnicas de segmentação, renderam dados na forma de pixels ao longo de um limite ou pixels incluidos em uma região. Embora estes dados às vezes são diretamente usados obter descrição (como determinar a textura de uma região), a prática normal é usar esquemas que compactam os dados em representações que são consideravelmente mais úteis na computação descritiva. Aproximações de representação:

São usados, cadeia de códigos para apresentar um limite por uma sucessão conectada de segmentos de linha reta especificada de comprimento e direção. Tipicamente, esta representação é baseada nos 4 ou 8 conectores dos segmentos. A direção de cada segmento é codificada usando um esquema numerando iniciando com 0 em sentido anti-horário mostrado na figura 1.

Imagens digitais normalmente são adquiridas e processadas em um formato de grade com espaçamento iguais nas direções x e y, assim uma cadeia de código pode ser gerado seguindo um limite, seguindo a direção no sentido horário, e atribuindo uma direção aos segmentos que conectam todo par de pixels. Este método geralmente é inaceitável por duas razões principais:

Uma aproximação freqüentemente usada para evitar os problemas há pouco discutidos é a amostragem do limite selecionando uma grade mais espaçada, como a figura 2 (a). Então, onde o limite é cruzado um ponto limite é atribuído a cada nó da grande grade, dependendo da proximidade do nó ao limite original, como figura 2 (b). O limite da amostragem obtido deste modo, pode ser representado então por 4 ou 8 códigos, figura 2 (c) e (d), respectivamente. O ponto de partida nas figuras (c) e (d) é o ponto, conforme a direção a ser tomada é indicada o número correspondente, sempre em sentido horário.

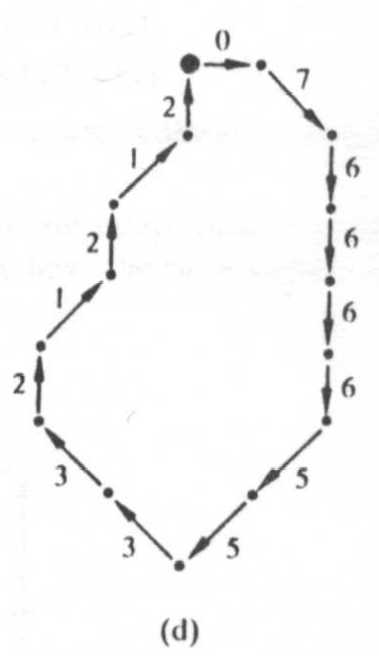
Figura 2: a) limite digital com grade de amostragem supreposto, b) resultado da amostragem,
c) cadeia de código de 4 direções, d) cadeia de código de 8 direções

A representação de limite na figura c é a cadeia de código 0033 ...01, e na figura d o código 076 ...1,2. Como poderia ser esperado, a precisão da representação de código resultante depende do espaçamento da grade testada.

A cadeia de código de um limite depende do ponto de partida. Porém, o código pode ser normalizado por um procedimento direto: porque um código de cadeia gerado começado em uma posição arbitrária, é tratado como uma sucessão circular de direção de números, redefinindo o ponto de partida de forma que a sucessão resultante de números redefina a sucessão resultante.

Pode-se normalizar a rotação usando a primeira diferença do código de cadeia em vez do próprio código. Esta diferença simplesmente é obtida contando (à esquerda) o número de direções que separam dois elementos adjacentes do código. Por exemplo, a primeira diferença usando cadeia de código de 4 direções 10103322 é 3133030.

Se nós escolhermos para tratar o código como uma sucessão circular, então o primeiro elemento da diferença é computado usando a transição entre o último e primeiro componentes da cadeia. Aqui, o resultado é 33133030. Normalização de tamanho pode ser alcançada alterando o tamanho da grade de amostragem.

Um limite digital pode ser aproximado com precisão arbitrária por um polígono. Para uma curva fechada, a aproximação exata quando o número de segmentos no polígono é igual ao número de pontos no limite assim que cada par de pontos adjacentes define um segmento no polígono. Na prática, a meta de uma aproximação polígonal é capturar a essência da forma do limite com menos segmentos poligonais possíveis. Este problema é em geral não trivial e pode se transformar em uma procura interativa demorada. Porém, várias técnicas de aproximação poligonais de complexidade simples e exigências de processamento são bem adaptadas para aplicações de processamento de imagem.
O método de busca de polígonos de perímetro mínimo, é explicado por este exemplo:
Suponha que é incluído um limite de células concatenadas fixas, como figura 3 (a). Isto ajuda a visualizar este cerco como duas paredes correspondendo ao exterior e dentro dos limites da viagem da célula e encontra no limite do objeto com uma faixa de borracha contida dentro das paredes. Se a faixa de borracha é permitida encolher isto leva a forma mostrada na figura 3 (b), produzindo um polígono de perímetro mínimo que ajusta a geometria estabelecida pela tira da célula. Se cada célula cercar apenas um ponto no limite, o erro em cada célula entre o limite original e a aproximação da faixa de borracha iria ser de raiz de 2d, onde d seria a distância entre pixels. O erro pode ser reduzido pela metade, forçando cada célula a ser centrada em seu pixel correspondente.

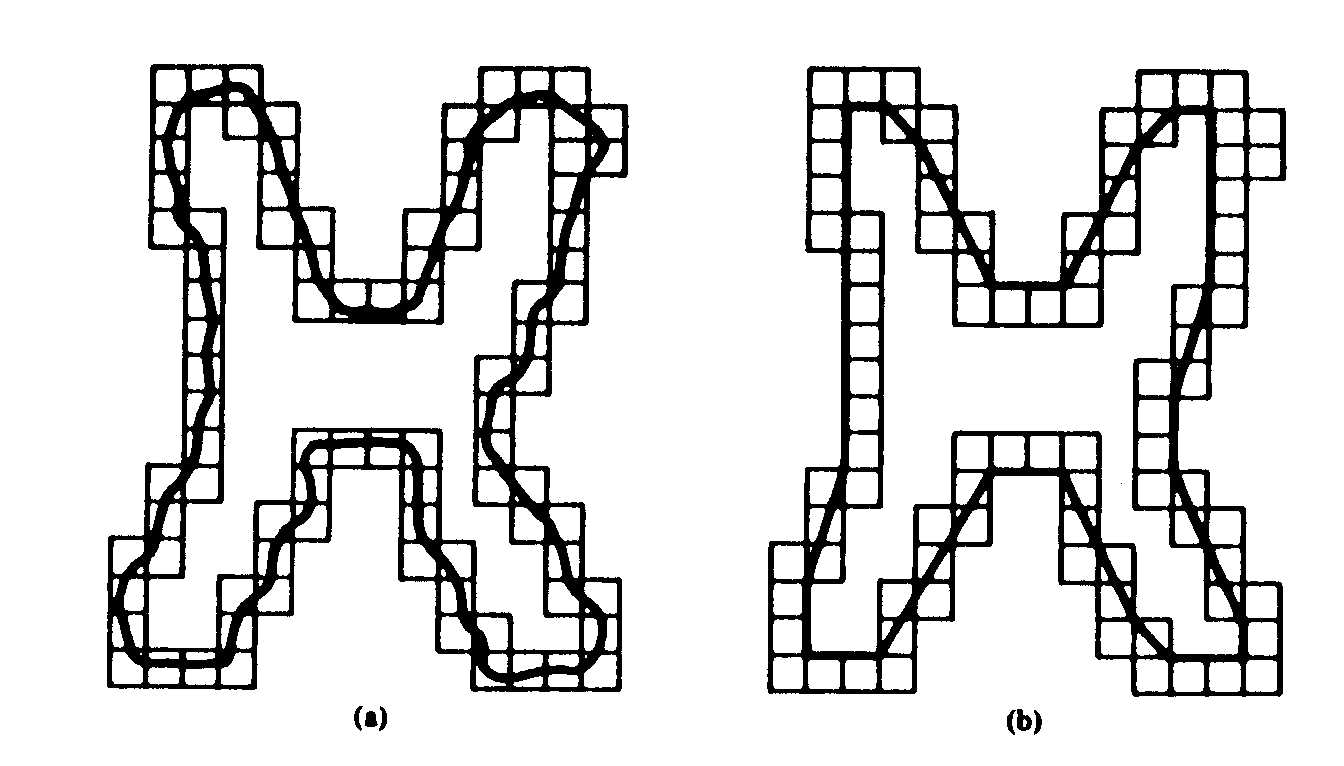
Figura 3: (a) Limite de objeto incluído por célula, (b) polígono de perímetro mínimo

Para limite fechado, os melhores pontos de partida são normalmente os dois pontos mais distantes no limite. Por exemplo, figura 4 (a), é mostrado um limite de objeto, a figura (b) mostra uma subdivisão deste limite (linha sólida) sobre seus pontos mais distantes. O ponto c na figura (b), marca a distância perpendicular mais longa no segmento de fundo. A figura (c) mostra o resultado usando procedimento de separação com um limiar (entrada) igual para 0.25 vezes a duração da linha de ab. Como nenhum ponto nos segmentos de limite novos tem uma distância perpendicular (para seu segmento de linha direta correspondente) excedendo este limiar, o procedimento termina com o polígono mostrado na figura (d ).

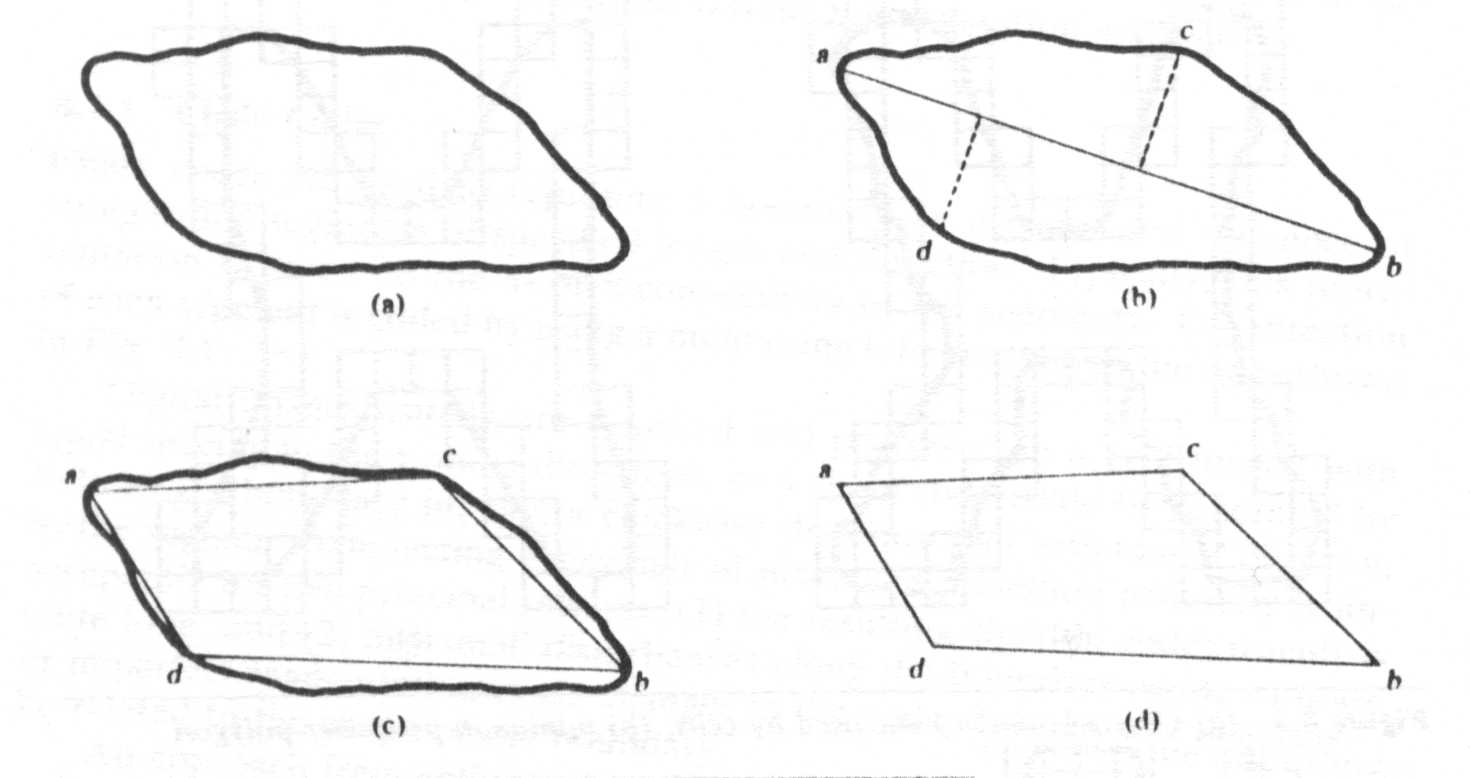
Figura 4: (a) limite original, (b) limite dividido em segmentos baseado em computações de distância,
(c) união de vertices, (d) polígono resultante

Decompondo freqüentemente um limite em segmentos pode ser útil. A decomposição reduz a complexidade do limite e assim simplifica o processo de descrição. Esta aproximação é particularmente atraente quando o limite contém um ou mais concavidades significantes que levam informação da forma.

Neste caso de uso da armação de covexa de uma região fechada pelo limite uma ferramenta poderosa é uma decomposição robusto do limite.

A armação convexa H de um arbitrário S fixo é o menor convexo fixo que contém S. A diferença fixa H - S é chamado a diferença convexa D do S fixo. Para perceber como estes conceitos poderiam ser usados para dividir um limite em segmentos significantes, considere a figura 5 (a) que mostra um objeto (S fixo) e sua deficiência convexa (regiões sombreadas). O limite de região pode ser partiticionada seguindo o contorno de S e marcando os pontos aos quais uma transição é feita dentro ou fora de um componente de deficiencia convexa. A figura 5 (b), mostra o resultado neste caso. Note isso em princípio, este esquema é independente de tamanho de região e da orientação.

Na pratica, limites digitais tendem a ser irregulares por causa de digitalização, ruídos, e variações em segmentação. Estes efeitos normalmente resultam em uma deficiência convexa que tem componentes pequenos, sem sentido difundida e randomizada ao longo do limite. Em lugar de tentar ordenar estas irregularidades pós-processo, a prática comum é suavizar um limite anterior para dividir.

Há vários modos para fazer assim. Um modo é atravessar o limite e substituir as coordenadas de cada pixel pelo coordenadas comuns de M de seus vizinhos ao longo do limite. Esta aproximação trabalha para irregularidades pequenas, mas é demorado e de difícil controle. Valores grandes de M podem resultar em análise excessiva, considerando que valores pequenos de M poderiam não ser suficientes em alguns segmentos do limite. Uma técnica mais áspera é usar uma aproximação poligonal, como anteriormente discutido, encontrando a deficiência convexa de uma região.

A concepção de uma armação convexa e sua deficiência são igualmente usadas para descrever uma região inteira, como também um pouco de seu limite. Por exemplo, descrição de uma região poderia estar baseado em sua área e a área de sua deficiência convexa, o número de componentes na deficiência convexa, a localização relativa destes componentes, e assim por diante.

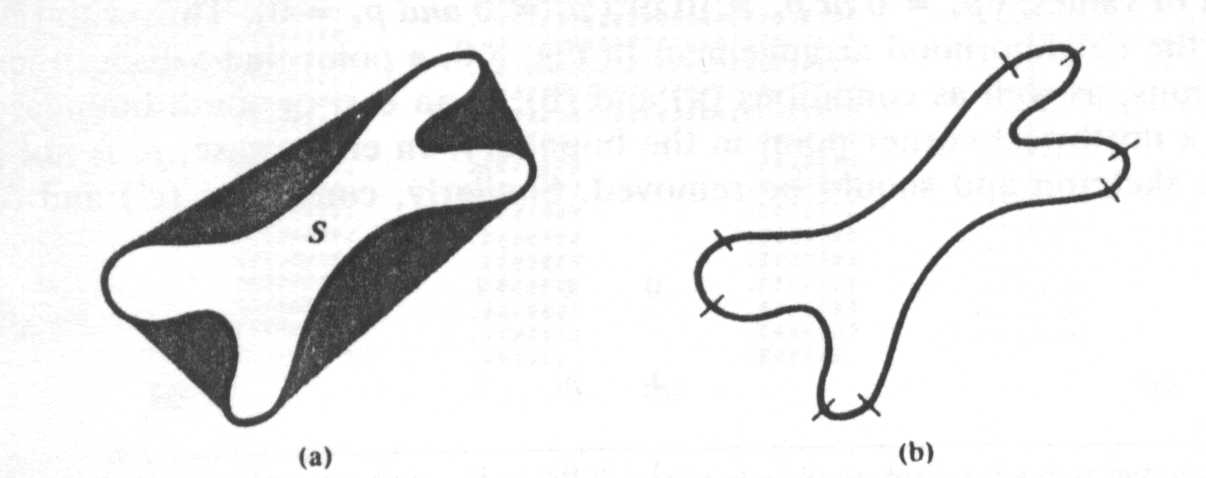
Figura 5: (a) Região (S) e deficiência convexa (sombreado); (b) limite dividido

Uma aproximação importante para representar a forma estrutural de uma região plana é reduzir isto para um gráfico. Esta redução pode ser realizada obtendo o esqueleto de uma região por um algoritmo de redução (também chamado esqueletonização). Procedimentos de redução representam um papel central em uma parte de problemas de processamento de imagem, variando de inspeção automatizada de circuitos impressos a contagem de fibras de amianto em filtros de ar.

Apesar de que o TAPETE de uma região se renda intuitivamente com quer a esqueletonização, a implementação direta daquela definição é tipicamente proibido computacionalmente. A implementação envolve calcular a distância de todo ponto interior para todo ponto no limite de uma região. Numerosos algoritmos tem se proposto para melhorar a eficiência computacional enquanto tenta-se produzir uma representação do eixo da mediana de uma região.

Observe o algoritmo de emagrecimento de regiões binárias. É assumido que ponto de região tem valor 1 e o fundo tem valor 0. O método consiste em passagens sucessivas de dois passos básicos aplicadas aos pontos de contorno de determinada região, onde um ponto de contorno é qualquer pixel com valor 1 e tendo pelo menos octo-vizinhos com valor 0. Com referência para os octo-vizinhos,definição mostrada na figura 6.

1º passo marca um ponto de contorno p para apagamento se as condições seguintes estão satisfeitas:

p9	p2	p3
p8	p1	p4
p7	p6	p5

e S(p1) é o número de 0-1 transições na sequencia ordenada de p2, p3,..., p8, p9, p2. Por exemplo, N(p1)="4" e S(p1)="3" . Conforme figura 7.

No 2º passo, condições (a) e (b) permanecem o mesmo, mas condições (c) e (d) é mudada para:

O passo 1 é aplicado a todo pixel de borda na região binária debaixo de consideração. Se um ou mais de condições de (a) até (d) é violada, o valor do ponto em questão não é mudado. Se todas as condições estão satisfeitas o ponto faz sinal para apagamento. Porém, o ponto não é apagado até todos os pontos de borda forem processado. Esta demora previne a mudança da estrutura dos dados durante execução do algoritmo. Depois do passo 1 for aplicado a todos os pontos de borda, esses que foram sinalizados são apagados (mudando para 0). Então, passo 2 é aplicado ao dados resultante, exatamente da mesma forma como o passo 1.

Condição (a) é violada quando o contorno do ponto p1, tem um ou sete octo-vizinhos com valor 1. Tendo só um vizinho implica que, p1 é o ponto extremo de uma redução, e obviamente não deve ser apagado. Apagando p1 se tivesse sete vizinhos causariam erosão na região. Condição (b) é violado quando é aplicado a pontos em um golpe 1 pixel espesso. Conseqüentemente esta condição previne disconecção de segmentos de um esqueleto durante a operação de redução. Condição (c) e (d) é simultaneamente satisfeita pelo jogo mínimo de valores: (p4="0" ou p6="0)" ou (p2="0" e p8="0)." Assim com referência para o arranjo de vizinhança na figura 8.8, um ponto que satisfaz estas condições, como também condições (a) e (b), é um ponto de limite leste ou sul ou um ponto de canto noroeste no limite. Em qualquer caso, p1 não são parte do esqueleto e deveriam ser removidos. Semelhantemente, condições (c') e (d') está simultaneamente satisfeito pelo jogo mínimo seguinte de valores: (p2="0" ou p8="0)" ou (p4="0" e p6="0)." Estes correspondem a norte ou limite oeste aponta, ou um ponto de canto de sudeste. Note aqueles pontos de canto de nordeste têm p2="0" e p4="0" e assim satisfaz condições (c) e (d), como também (c') e (d'). O mesmo é verdade para pontos de canto sudoestes que têm p6="0" e p8="0."

0	0	1
1	p1	0
1	0	1

A figura 8 (a) mostra o resultado de aplicar o passo 1 do algoritmo emagrecendo para o limite de uma região simples. Os pontos indicam os pontos sinalizados e subseqüentemente removidos ao término de passo 1. Na figura 8 (b) mostra os resultados obtidos com o passo 2, e na figura 8 (c) mostra que o esqueleto obtido depois de várias interações por estes dois passos. O esqueleto de uma região com propriedades menos-regulares é mostrado em figura 9.

Figura 8: (a) Resultado do passo 1 do algoritmo emagrecendo durante a primeiro interação por uma região;
(b) resultado do passo 2; (c) resultado final. (De Zhang e Suen [1984].)