ine 5341

Programa

OpenGL

Trabalhos 2001

Trabalhos 2002

Links

Bibliografia

Plano de Ensino

 Parte II - Computação Gráfica Avançada

Visualização Realística em 3D, z-Buffering e Raytracing


z-Buffer: O Algoritmo de Superfícies Visíveis baseado em Buffer de Profundidade

Este material se baseia em parte nas On-Line Computer Graphics Notes, Computer Graphics Group, Computer Sciences Department, University of California, Davis, originalmente escritas por Ken Joy.

Para que possamos realizar a representação acurada e realista de um modelo tridimensional complexo, em uma cena contendo vários objetos diferentes, é necessário que aquelas superfícies normalmente invisíveis de um determinado ângulo ou ponto no mundo sejam também renderizadas invisíveis no computador.  Este problema é normalmente chamado de problema de superfície visível (visible-surface problem), quando nosso objetivo é determinar quais superfícies de um objeto são visíveis de um determinado ângulo, ou problema de superfície oculta (hidden-surface problem), quando nosso objetivo é determinar quais superfícies estão invisíveis neste momento. Ele foi um problema fundamental abordado pela pesquisa em Computação Gráfica durante muito tempo. Para ilustrar o que são os efeitos desejados de um método dessa família de algoritmos, basta observar os dois desenhos abaixo mostrando a mesma estrutura, uma vez em modelo de arame e outra em modelo de sólidos/superfícies. A figura da direita nos fornece de imediato muito mais informação sobre as posições relativas dos objetos na cena do que o modelo de arame da esquerda. 

\includegraphics {figures/visible-surface-1}

De todos os algoritmos para determinação de superfície visível, o buffer de profundidade ou zBuffer é talvez o método mais simples e com certeza o mais amplamente utilizado. Em função disso, vamos nos limitar a descrever este método neste texto.

O princípio de funcionamento do algoritmo é muito simples: Para todo pixel na Viewport nós mantemos um registro da profundidade (em termos de coordenada z) do objeto na cena que estiver mais próximo, além de um registro da intensidade, cor, etc, que deveria ser utilizada ao se mostrar este ponto em particular na tela do computador. Toda vez que um novo polígono é processado, um valor de z e de intensidade são calculados para cada pixel que estiver dentro dos limites do polígono. Se o valor de coordenada z obtido para oaquele polígono for inferior ao valor de z armazenado para aquele pixel no buffer, então este objeto está mais próximo do que algum objeto anteriormente renderizado naquela posição e vai ocultar aquele objeto. Neste caso, substituímos o valor armazenado naquela posição do buffer por este novo valor. 

Se não for realizado nenhum cálculo de radiosidade ou outra técnica de raytracing mais avançada, após o processamento de todos os polígonos da cena, o buffer de intensidade/cor resultante representará exatamento os valores dos pixels da Viewport e pode ser visualizado sem mais nenhuma transformação.

O Método z-Buffer

O algoritmo z-Buffer trabalha em Coordenadas de Vídeo ou Viewport (espaço de dispositivo) e pode ser implementado facilmente como uma extensão/modificação de um algoritmo de conversão por varredura. Uma versão simples de um algoritmo deste tipo vimos no capítulo anterior.  O z-Buffer ou Buffer de Profundidade, estrutura de dados da qual o método tira seu nome, é uma matriz  n x n  na qual o elemento (i,j)  corresponde ao pixel (i,j). Esta matriz contém o valor de z em Coordenadas do Mundo (espaço de imagem) do objeto correntemente visível  naquele pixel. Além disso, existe outra matriz n x n cujos elementos correspondem à cor ou intensidade luminosa que é para ser atribuída àquele pixel. 

Vamos mostrar a operação do z-Buffer considerando um exemplo bidimensional com uma viewport-linha unidimensional com resolução de 8x1 pixels e com polígonos representados como segmentos de retas, tal qual sugere [Joy93]. É um exemplo extremamente simplista, pois elimina o significado do eixo y, mas os passos a serem executados são praticamente idênticos à execução do algoritmo para três dimensões e dessa forma ficará mais fácil para o leitor compreender. 

Inicialização do z-Buffer

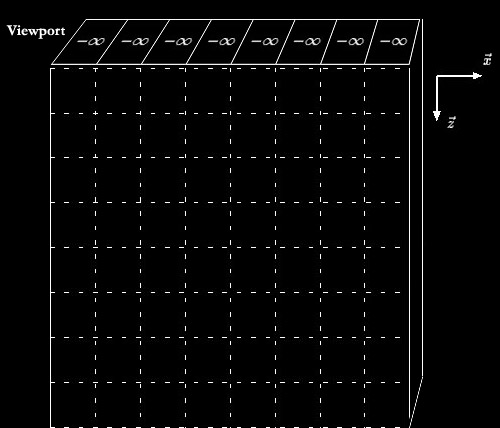
O buffer de profundidade é inicializado atribuindo-se a todos os seus elementos o valor $ -\infty$, que pode ser representado por algum valor negativo extremamente alto, já que não renderizamos polígono algum até este momento. A matriz de cores ou intensidades luminosas (para renderizações em preto e branco) é inicializada atribuindo-se a todos os seus pixels a cor preta.  Imagine o z-Buffer como representando o volume de espaço "atrás" do buffer, na direção z, tal qual está desenhado na figura abaixo.

    \includegraphics {figures/z-buffer-0}
Mapeamento da Profundidade dos Objetos na Cena

O próximo passo é mapear, pixel a pixel, a profundidade de cada objeto da cena que se encontra atrás daquele pixel. Tome cada um dos polígonos, execute a conversão por varredura e, durante esta conversão, execute os passos seguintes:

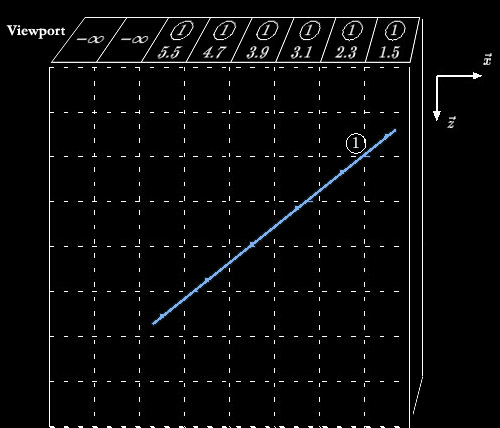
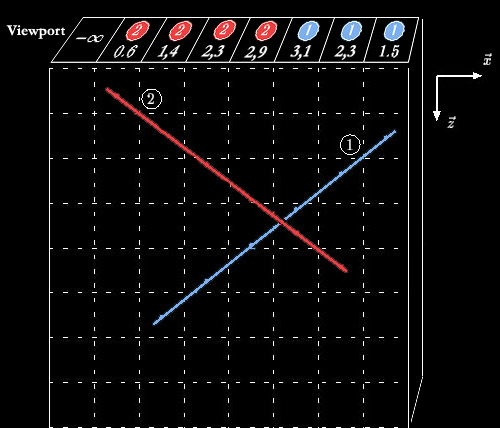
Passo 1 - Verificação de intersecção. Para cada pixel, determine os polígonos da cena cuja conversão de varredura resultou em um elemento com as coordenadas x,y deste pixel. 

Passo 2 - Determinação da ordem de ocultação. Para todos os polígonos da cena, determine para cada pixel (i,j) que intercepta o polígono, se o valor z em Coordenadas do Mundo (eixo z do desenho acima) deste polígono na posição do pixel é maior do que o valor z armazenado no z-Buffer. Se for maior, calcule a cor e outros valores associados a este pixel e os insira na entrada (i,j) da matriz de cor e insira o valor z do polígono naquele ponto na posição (i,j) do z-Buffer. Senão, não faça nada.

Exemplo: Se inserirmos uma linha, como mostrado abaixo, nós registramos  valor de profundidade de cada pixel e obtemos as valores mostrados na figura:
\includegraphics {figures/z-buffer-1}
Se inserimos uma segunda linha e aplicamos o algoritmo acima novamente, vemos que o z-Buffer foi atualizado e mostra o índice da linha "da frente",  visível, naquele pixel e o valor de profundidade da linha naquele ponto.

Algoritmo z-Buffer

Podemos descrever na forma de um pseudocódigo bastante simples o que descrevemos acima.

Algoritmo Z-Buffer

Dados: 
  Lista of polígonos {P1, P2, ..., Pn} 
  Matriz z-buffer[x,y] inicializado com$ -\infty$
  Matriz Intensidade[x,y] 
início
      para cada polígono P na lista de polígonos  faça { 
          para cada pixel (x,y) que intercepta P faça { 
              calcule profundidade-z de P na posição (x,y) 
              se prof-z < z-buffer[x,y] então { 
                 Intensidade[x,y] = intensidade de P em (x,y) 
                 z-buffer[x,y] = prof-z 
               } 
           } 
      } 
      Desenhe Intensidade
fim

Uma vez que todo polígono pode ser dividido em um conjunto de trapézios (se aceitarmos o triângulo como um trapézio degenerado de topo zero) , basta-nos considerar o algoritmo do zBuffer sobre trapézios. Para tanto podemos diretamente modificar o algoritmo de renderização descrito no capítulo sobre Conversão por Varredura deste texto ou então um dos algoritmos de rasterização mais avançados encontrados nas rasterization notes da UC Davis para criar  na íntegra o algoritmo de zBuffer descrito acima. Pode-se utilizar diretamente os procedimentos de rasterização e de atualização de vídeo implementados pelo algoritmo de conversão que for ser utilizado.

Toques para Quem quer ir mais Fundo

Um bom livro para você ler e aprofundar este assunto é a segunda edição do Interactive Computer Graphics de Foley, van Damm e outros. Veja a seção de bibliografia deste texto para a referência detalhada. Não perca tempo procurando a primeira edição deste livro, que este assunto não é abordado nela. 

Na Internet, de longe, a melhor fonte de informação séria e confiável neste assunto são as On-Line Computer Graphics Notes, mantidas por professores e estudantes do Computer Graphics Group, Computer Science Department, na UC Davis.