Estruturas de Dados
[RTF] [PostScript]
7. Análise de Algoritmos
Introdução
- O estudo de Estruturas de Dados é basicamente o estudo
de métodos de organização de grandes quantidades de
dados.
Estes métodos incluem:
- formas de organizá-los (estruturas) e
- técnicas para manipulá-los (algoritmos básicos).
- Pilhas, Listas e Filas são estruturas de dados típicas.
- Para manipular estas estruturas, como inserir elementos, retirar elementos,
ordenar elementos, necessitamos de algoritmos.
- Estes algoritmos podem ser implementados de muitas maneiras. Algumas
simples e diretas outras não tão simples, porém engenhosas
e outras ainda complicadas e envolvendo muitas operações.
- Quando trabalhamos com quantidades muito grandes de dados, um projeto
ruim de um algoritmo para manipular uma estrutura de dados pode resultar
num programa que tem um tempo de execução inviável.
- Quando estudamos algoritmos, um aspecto que devemos considerar , além
de sua correção, é a análise da sua eficiência.
A análise de algoritmos pode ser definida como o estudo
da estimativa do tempo de execução dos algoritmos (M.A.Weiss).
7.1. Idéias básicas
- Um algoritmo é um conjunto finito de passos que devem ser seguidos
com um conjunto de dados de entrada para se chegar a solução
de um problema.
- Um problema pode geralmente ser resolvido por muitos algoritmos diferentes.
Ex.: Cálculo da potência xn de um número
inteiro x.
inteiro potência (x, n)
inteiro x, y, n, j;
início
i <- n;
y <- 1;
enquanto (i > 0) faça
y <- y * x;
i <- i - 1;
fim enquanto
retorne y;
fim
inteiro potência_recursiva (x, n)
início
se (n = 1) então retorne x;
y <- potência_recursiva ( x, (n div 2) );
se (ímpar(n)) então
retorne x*y*y;
senão
retorne y*y;
fim se
fim
O fato de existir um algoritmo para resolver um problema, não
implica necessariamente que este problema possa realmente ser resolvido
na prática.
Há restrições de tempo ou de espaço de memória.
Ex.: Calcular todas as possíveis partidas de xadrez.
- Um algoritmo é uma idéia abstrata de como resolver um
determinado problema. Ele é, a princípio, independente da
máquina que o executará e de suas características.
- Um programa é uma implementação de um algoritmo
em uma linguagem particular e que será executado em um computador
particular.
- Um programa está sujeito às limitações
físicas da máquina onde será executado, como capacidade
de memória, velocidade do processador e dos periféricos,
etc.
O tempo que a execução de um programa toma é uma
grandeza física que depende:
- Do tempo que a máquina leva para executar uma instrução
ou um passo de programa.
- Da natureza do algoritmo, i.é, de quantos passos são
necessário para se resolver o problema para um dado.
- Do tamanho do conjunto de dados que constitui o problema.
7.2. Problema básico
na Análise de Algoritmos:
- Necessitamos definir uma forma de criar uma medida de comparação
entre diferentes algoritmos que resolvem um mesmo problema, para:
- Podermos saber se são viáveis
- Podermos saber qual é o melhor algoritmo para a solução
do problema.
- Para fazermos isso, abstraímos de um computador em particular
e assumimos que a execução de todo e qualquer passo de um
algoritmo leva um tempo fixo e igual a uma unidade de tempo.
- O tempo de execução em um computador particular não
é interessante.
- Muito mais interessante é uma comparação relativa
entre algoritmos.
Modelo de computação: As operações
são todas executadas seqüencialmente. A execução
de toda e qualquer operação toma uma unidade de tempo. A
memória do computador é infinita.
7.3. Complexidade de Tempo
- Podemos expressar de forma abstrata a eficiência de um algoritmo,
descrevendo o seu tempo de execução como uma função
do tamanho do problema (quantidade de dados). Isto é chamado de
complexidade de tempo
Exemplo: Ordenação de um Vetor
7.3.1. Primeiro caso: Bubblesort
Bubblesort é o mais primitivo dos métodos de ordenação
de um vetor. A idéia é percorrer um vetor de n posições
n vezes, a cada vez comparando dois elementos e trocando-os caso o primeiro
seja maior que o segundo:
ordenaBolha /* Bubblesort */
inteiro i,j,x,a[n];
início
para i de 1 até n faça
para j de 2 até n faça
se (a[j-1]>a[j]) então
x <- a[j-1];
a[j-1] <- a[j];
a[j] <- x;
fim se
fim para
fim para
fim
A comparação (a[j-1]>a[j]) vai ser executada
n*(n-1) vezes. No caso de um vetor na ordem inversa, as operações
da atribuição triangular poderão ser executadas até
3*n*(n-1) vezes, já uma troca de elementos não significa
que um dos elementos trocados tenha encontrado o seu lugar definitivo.
7.3.2. Segundo caso: StraightSelection
O método da seleção direta é uma forma intuitiva
de ordenarmos um vetor: escolhemos o menor elemento do vetor e o trocamos
de posição com o primeiro elemento.
Depois começamos do segundo e escolhemos novamente o menor dentre
os restantes e o trocamos de posição com o segundo e assim
por diante.
seleçãoDireta
inteiro i,j,k,x,a[n];
início
para i de 1 até n-1 faça
k <- i;
x <- a[i];
para j de i +1 até n faça
se (a[j] < x) então
k <- j;
x <- a[k];
fim se
fim para
a[k] <- a[i];
a[i] <- x;
fim para
fim
Neste algoritmo o número de vezes que a comparação
(a[j] < x) é executada é expresso por (n-1)+(n-2)+...+2+1
= (n/2)*(n-1).
O número de trocas a[k] <- a[i]; a[i] <- x é
realizado no pior caso, onde o vetor está ordenado em ordem inversa,
somente n-1 vezes, num total de 2*(n-1).
7.3.3. Interpretação
Como ja'foi dito, a única forma de se poder comparar dois algoritmos
é descrevendo o seu comportamento temporal em função
do tamanho do conjunto de dados de entrada, Talgoritmo = f(n),
onde n é o tamanho dos dados.
Assim, se tomarmos as operações de troca de valores como
critério-base, podemos dizer que:
Tbubblesort = 3*n*(n-1) sempre e
Tstraightselection = 2*(n-1) para o pior caso.
- O que nos interessa é o comportamento assintótico de
f(n), ou seja, como f(n) varia com a variação de n.
- Razão: Para mim é interessante saber como o algoritmo
se comporta com uma quantidade de dados realistica para o meu problema
e o que acontece quando eu vario esses dados. Exemplo: Se
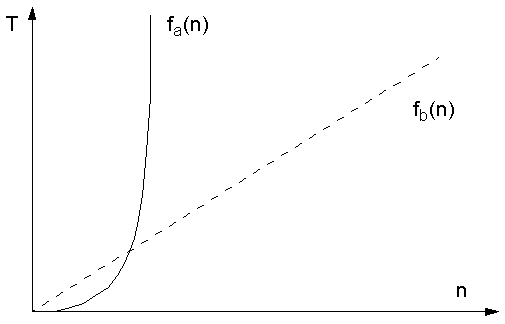
eu tenho dois algoritmos a e b para a solução de um problema.
Se a complexidade de um é expressa por fa(n) = n2
e a do outro por fb(n) = 100*n. Isto significa que o algoritmo
a cresce quadraticamente (uma parábola) e que o algoritmo b cresce
linearmente (embora seja uma reta bem inclinada).
Se eu uso esses algoritmos para um conjunto de 30 dados, o segundo com
Tb=3000 é pior do que o primeiro com Ta=900.
Se eu os uso para um conjunto de 30.000 dados, porém, terei Ta=900.000.000
e Tb=3.000.000.
- Isto porque o comportamento assintótico dos dois
é bem diferente.
Podemos ver isto expresso no gráfico abaixo:
7.4. Interpretação
da Complexidade de Tempo
O gráfico acima nos mostra qual é o aspecto essecial que
deve ser expresso pelo cálculo de complexidade:
|
Qual é o comportamento assintótico
predominante de um algoritmo
em função do tamanho do
conjunto de dados a ser processado.
|
Por exemplo:
- se é linear,
- polinomial (quadrático, cúbico, etc),
- logarítmico ou
- exponencial.
7.4.1. Análise Assintótica
- Para a análise do comportamento de algoritmos existe toda uma
terminologia própria.
- Para o cálculo do comportamento de algoritmos foram
desenvovlidas diferentes medidas de complexidade.
- A mais importante delas e que é usada na prática é
chamada de Ordem de Complexidade ou Notação-O ou Big-Oh.
- Definição (Big-Oh): T(n) =
O(f(n)) se existem constantes c e n0 tais que
T(n)c.f(n) quando nn0.
- A definição indica que existe uma constante c
que, faz com que c.f(n) seja sempre pelo menos tão grande
quanto T(n), desde que n seja maior que um n0.
- Em outras palavras: A Notação-O me fornece a Ordem de
Complexidade ou a Taxa de Crescimento de uma função .
- Para isso, não consideramos os termos de ordem inferior da complexidade
de um algoritmo, apenas o termo predominante.
Exemplo: Um algoritmo tem complexidade T(n) = 3n2 +
100n.
Nesta função, o segundo termo tem um peso relativamente
grande, mas a partir de n0 = 11, é o termo n2
que "dá o tom" do crescimento da função:
uma parábola. A constante 3 também tem uma
influência irrelevante sobre a taxa de crescimento da função
após um certo tempo.
Por isso dizemos que este algoritmo é da ordem de n2 ou que tem
complexidade O(n2).
7.4.2. Diferentes Tempos de Execução
Problema da Subseqüência de Soma Máxima: Dada
uma seqüência de números a1, a2, ... , an, positivos
ou negativos, encontre uma subseqüência aj,...,ak dentro desta
seqüência cuja soma seja máxima. A soma de uma seqüência
contendo só números negativos é por definição
0.
Exemplo: Para a seqüência -2,
11, -4, 13, -5, -2, a resposta é 20
(a2,a3,a4).
Este problema oferece um bom exemplo para o estudo de como diferentes
algoritmos que resolvem o mesmo problema possuem diferentes comportamentos,
pois para ele existem muitas soluções diferentes.
Abaixo, um exemplo dos tempos de execução dos diferentes
algoritmos da subseqüência de maior soma:

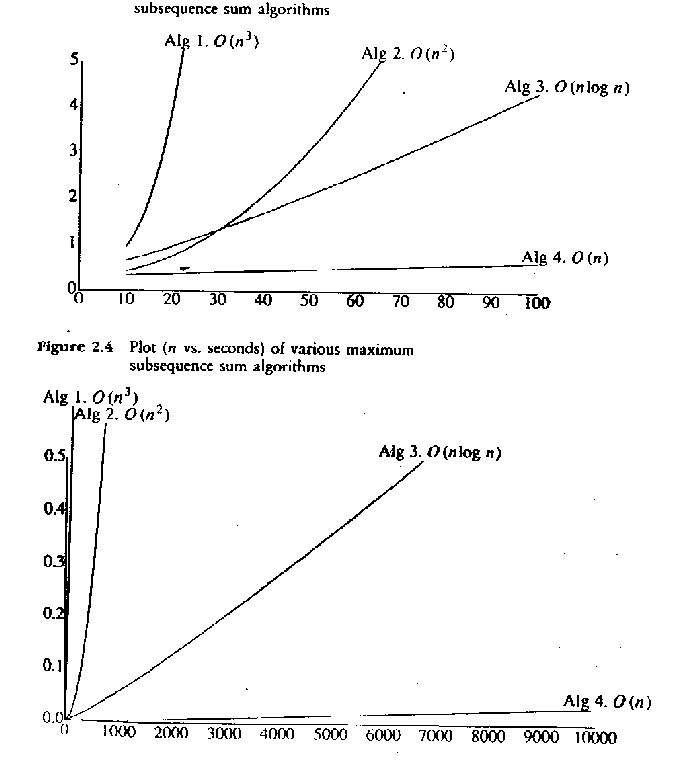
7.4.3. Alguns exemplos do comportamento de diferentes
algoritmos para a solução do problema da subseqüência
de soma máxima:
7.5. Cálculo
da Complexidade de Tempo
Um exemplo intuitivo: Cálculo de
inteiro somaCubos (inteiro n)
inteiro i, somaParcial;
início
1 somaParcial <- 0;
2 para i de 1 até n faça
3 somaParcial <- somaParcial + i * i * i;
4 fim para
5 retorne somaParcial;
fim
Análise:
- As declarações não tomam tempo nenhum.
- A linha 4 também não toma tempo nenhum.
- As linhas 1 e 5 contam uma unidade de tempo cada.
- A linha 3 conta 4 unidades de tempo (2 multiplicações,
uma adição e uma atribuição) e é executada
n vezes, contando com um total de 4n unidades de tempo.
- A linha 2 possui custos implícitos de de inicializar o i ,testar
se é menor que n e incrementá-lo. Contamos 1 unidade para
sua inicialização, n + 1 para todos os testes e n para todos
os incrementos, o que perfaz 2n + 2 unidades de tempo.
- O total perfaz 6n + 4 unidades de tempo, o que indica que o algoritmo
é O(n), da Ordem de Complexidade n, ou seja, linear.
7.5.1. Regras para o cálculo
- Laços Para-Faça e outros:
O tempo de execução de um laço é, no máximo,
a soma dos tempos de execução de todas as instruções
dentro do laço (incluindo todos os testes) multiplicado pelo número
de iterações.
- Laços Aninhados:
Analise-os de dentro para fora.
O tempo total de execução de uma instrução
dentro de um grupo de laços aninhados é o tempo de execução
da instrução multiplicado pelo produto dos tamanhos de todos
os laços.
Exemplo O(n2):
para i de 1 até n
para j de 1 até n
k <- k + 1;
fim para
fim para
- Instruções Consecutivas:
Estes simplesmente somam, sendo os termos de ordem menor da soma ignorados.
Exemplo O(n)+O(n2) = O(n2):
para i de 1 até n
a[i] <- 0;
fim para
para i de 1 até n
para j de 1 até n
a[i] <- a[j] + k + 1;
fim para
fim para
- IF/THEN/ELSE:
Considerando-se o fragmento de código abaixo:
se cond então
expresssão1
senão
expressão2
fim se
o tempo de execução de um comando IF/THEN/ELSE nunca
é maior do que o tempo de execução do teste cond
em si mais o tempo de execução da maior dentre as expressões
expressão1 e expressão2.
Ou seja: se expressão1 é O(n3) e expressão2
é O(n), então o teste é O(n3) + 1 = O(n3).
- Chamada a Funções:
Segue obviamente a mesma regra dos laços aninhados: analise
tudo de dentro para fora. Ou seja: para calcular a complexidade de um programa
com várias funções, calcule-se primeiro a complexidade
de cada uma das funções e depois considere-se cada uma das
funções como uma instrução com a complexidade
de função.
- Recursão:
Recursão é a parte mais difícil da análise
de complexidade.
Na verdade existem dois casos: Muitos algoritmos recursivos mais simples
podem ser "linearizados", substituindo-se a chamada recursiva
por alguns laços aninhados ou por uma outra subrotina extra e eventualmente
uma pilha para controlá-la. Neste caso, o cálculo é
simples e pode ser feito depois da "linearização".
Em muitos algoritmos recursivos isto não é possível,
neste caso obtemos uma relação de recorrência que tem
de ser resolvida e é uma tarefa matemática menos trivial.
Exemplo de cálculo de complexidade em recursão: Fatorial
inteiro Fatorial (inteiro n)
início
se n <= 1 então
retorne 1;
senão
retorne ( n * Fatorial ( n - 1 ) );
fim se
fim
O exemplo acima é realmente um exemplo pobre de recursão
e pode ser "iterativisado" de forma extremamente simples com
apenas um laço para-faça:
inteiro FatorialIterativo (inteiro n)
inteiro i, fatorial;
início
fatorial <- 1;
para i de 2 até n faça
fatorial <- fatorial * i;
fim para
retorne fatorial;
fim
A complexidade de FatorialIterativo pode então
ser facilmente calculada e é evidente que é O(n).
O caso dos números de Fibonacci abaixo não é tão
simples e requer a resolução de uma relação
de recorrência:
inteiro Fibonacci (inteiro n)
início
se n <= 1 então
retorne 1;
senão
retorne ( Fibonacci(n-1) + Fibonacci(n-2)
);
fim se
fim
Observando o algoritmo, vemos que para n>= 2 temos um tempo de execução
T(n) = T(n-1)+T(n-2)+2.
A resolução desta relação nos mostra que Fibonacci
é O(()n)
7.5.2. Logaritmos e Outros no Tempo de Execução
- O aspecto mais complexo na análise de complexidade centra-se
em torno do logaritmo. Para analisar-se um algoritmo de complexidade logarítmica
e chegar-se a um resultado correto sobre a sua ordem exata de complexidade
é necessária uma certa experiência e algum "jeito"
matemático. Algumas regras de aproximação podem ser
dadas: 4 Algoritmos seguindo a técnica Dividir-Para-
Conquistar são muitas vezes n log n.
- Quando um algoritmo, em uma passada de uma iteração toma
o conjunto de dados e o divide em duas ou mais partes, tomando cada uma
dessas partes e a processando separada e recursivamente e depois juntando
os resultados, este algoritmo utiliza a técnica dividir-para-conquistar
e será possivelmente n log n.
- Um algoritmo é log n se ele toma um tempo constante O(1)
para dividir o tamanho do problema. Usualmente pela metade.
- A pesquisa binária já vista é um exemplo de log
n.
- Se o algoritmo toma tempo constante para reduzir o tamanho do problema
em um tamanho constante, ele será O(n).
- Algoritmos combinatórios são exponenciais: Se um algoritmo
testa todas as combinaçoes de alguma coisa, ele será exponencial.
Exemplo: Problema do Caixeiro Viajante
7.6. Checando a sua análise
Uma vez que a análise de complexidade tenha sido executada, é
interessante verificar-se se a resposta está correta e é
tão boa quanto possível.
Uma forma de se fazer isto é o procedimento pouco matemático
de se codificar o trecho de algoritmo cuja complexidade se tentou descrever
e verificar se o tempo de execução coincide com o tempo previsto
pela análise.
Quando n dobra, o tempo de execução se eleva de um fator
2 para algoritmos lineares, fator 4 para quadráticos e 8 para cúbicos.
Programas logarítmicos só aumentam o seu tempo de execução
de uma constante a cada vez que n dobra. Algoritmos de O(n log n) tomam
um pouco mais do que o dobro do tempo sob as mesmas circunstâncias.
Estes aumentos podem ser difíceis de se detectar se os termos
de ordem inferior têm coeficientes relativamente grandes e n não
é grande o suficiente. Um exemplo é o pulo tempo de execução
para n=10 do para n=100 em algumas implementações do problema
da subseqüência de soma máxima.
Distinguir programas n log n de programas lineares só em evidência
de tempo de execução pode também ser muito difícil.
Uma boa praxe é, caso o programa não seja exponencial
(o que você vai descobrir muito rápido), fazer alguns experimentos
com conjuntos maiores de dados de entrada
7.7. Exercício:
Calcule a Complexidade


Algoritmo extraído de: Márcia
de Aguiar Rabuske,; Introdução à Teoria
de Grafos, Editora da UFSC, 1990.






