Capítulo 9
Ordenação
[RTF]
[PowerPoint] [PostScript]
9.1 Introdução
à Ordenação
9.2 Quicksort
9.3 HeapSort
9.4 Exercícios
9.1 Introdução
à Ordenação
-
A noção
de um conjunto de dados ordenados é de considerável importância
na nossa vida quotidiana e por conseguinte também em computação
-
Exemplos:
-
Listas telefônicas,
-
Listas de clientes
de uma empresa,
-
Listas de peças
em um catálogo,
-
etc.
-
Algoritmos eficientes
para ordenar grandes quantidades de dados são de extrema importância.
-
Já vimos:
-
Algoritmos simples
e ineficientes, árvores
9.1.1 Conceitos básicos
em Ordenação
-
Arquivo
-
Um arquivo r de tamanho
n é uma seqüência de n ítens r[0], r[1], r[n-1].
-
Cada ítem em
um arquivo é chamado registro.
-
Um arquivo é
classificado por chave
-
se para cada registro
r[i] existe um uma parte de r[i], k[i] chamada chave de classificação.
-
se i<j implicar
que k[i] precede k[j] de acordo com algum critério qualquer predefinido
-
Exemplo:
-
Em um catálogo
telefônico o arquivo é o próprio catálogo,
-
Um registro é
uma entrada com nome, nº e endereço
-
O nome é a
chave.
Localização
de Execução:
-
Ordenação
interna é aquela realizada na memória principal do computador.
-
Ordenação
externa é aquela, onde os registros podem estar em uma memória
auxiliar (arquivo em disco).
Estabilidade:
-
Uma técnica
de ordenação é chamada estável se, para todos
os registros i e j, dado que k[i] é igual a k[j];
-
se r[i] precede r[j] no arquivo original,
-
então r[i] precederá r[j] no
arquivo classificado.
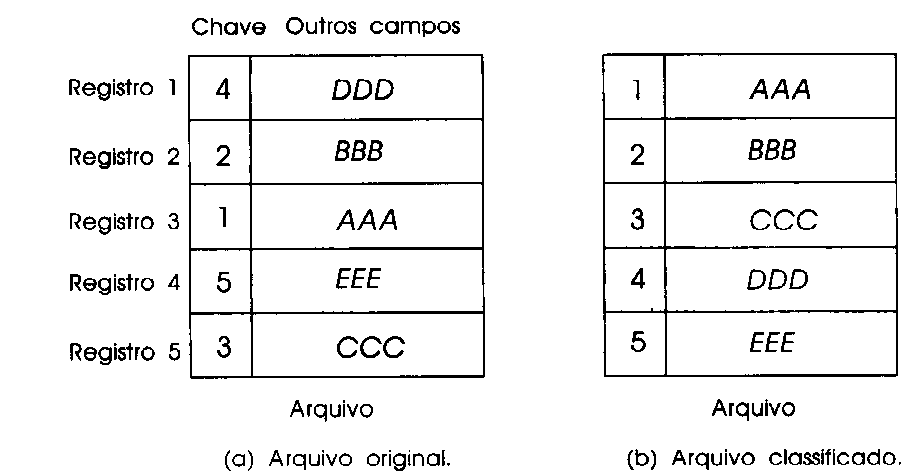
Uma ordenação
pode ocorrer sobre os próprios registros ou sobre uma tabela auxiliar
de ponteiros.
-
Classificação
direta é uma ordenação onde um arquivo é ordenado
diretamente, sendo os registros movidos de uma posição física
para outra.
-
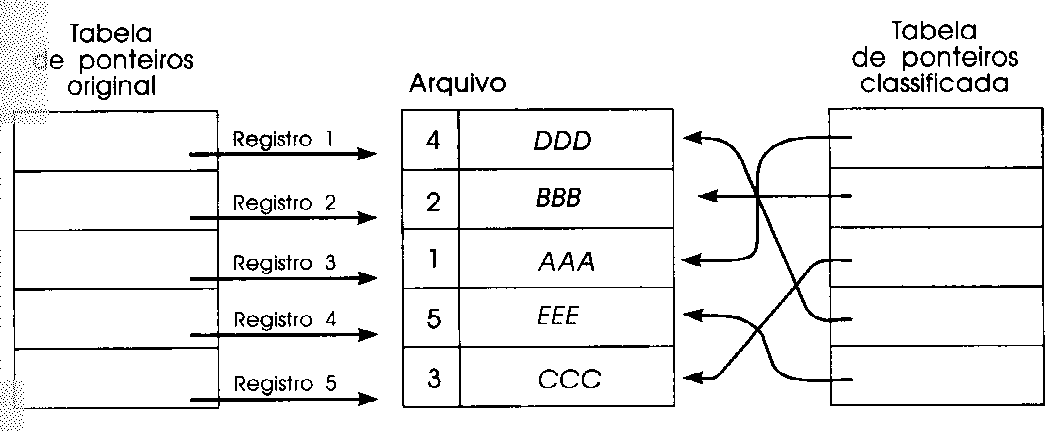
b) Classificação
por endereços é uma ordenação onde somente
uma tabela de ponteiros é ordenada, os registros em si não
são tocados.
9.1.2 Critérios
para Selecionar uma Ordenação
-
Eficiência no
Tempo
-
Se um arquivo é
pequeno (ex.: 20 registros) técnicas sofisticadas podem ser piores
-
Algoritmos complexos,
módulos grandes
-
Nº de vezes que
a ordenação será executada
-
Se vamos classificar
um conjunto de dados, mesmo grande, só uma vez, pode ser mais interessante
implementar um algoritmo simples.
-
Um programa que executa
ordenações repetidamente deve ser eficiente.
-
Esforço de
programação não deve ser uma desculpa para a utilização
de um algoritmo inadequado. Um sistema ineficiente não vai vender.
Eficiência de
Espaço
-
A técnica que
escolhi é compatível com as características de hardware
do ambiente para o qual a estou destinando?
9.1.2.1 Aspectos da
Eficiência de Tempo
-
O critério
básico para a determinação da eficiência de
tempo de um algoritmo não é a somente sua complexidade assintótica
-
Operações
críticas:
-
Operação
crítica é uma operação básica no processo
de ordenação. Ex.: a comparação de duas chaves
ou o deslocamento de um registro de uma posição de memória
para outra.
-
Um algoritmo que executa
todas as operações críticas na memória será
geralmente mais rápido, do que outro que executa algumas em memória
secundária (disco).
9.2
Quicksort
-
A ordenação
por troca de partição ou quicksort é provavelmente
o algoritmo de ordenação mais utilizado.
-
Divide and Conquer
-
Complexidade média
O(n log n)
-
Vantagens:
-
Simples de implementar
-
Bastante bem compreendido.
-
Extensas análises
matemáticas de seu comportamento já foram feitas
-
Desvantagens:
-
Complexidade pode
ser O(n2) no pior caso, em que o arquivo está ordenado
ou ordenado em ordem inversa.
-
Diferentes versões
melhoradas existem.
Algoritmo
Básico
-
Quicksort trabalha
particionando um arquivo em duas partes e então as ordenando separadamente.
-
Pode ser definido
recursivamente:
quicksort (tipoInfo : a[], inteiro : esq, dir)
inteiro i;
início
se dir > esq então
i <- particione(a, esq, dir);
quicksort(a, esq, i-1);
quicksort(a, i+1, dir);
fim se
fim
Os parâmetros
dir e esq delimitam os subarquivos dentro do arquivo original, dentro dos
quais a ordenação ocorre.
A chamada inicial
pode ser feita com quicksort(a, 1, N);
O ponto crucial é
o algoritmo de partição.
Particionamento
em Quicksort
-
O procedimento de
particionamento deve rearranjar o arquivo de maneira que as seguintes condições
valham:
-
o elemento a[i] está
em seu lugar final no arquivo para um i dado,
-
nenhum dos elementos
em a[esq],...,a[i-1] são maiores do que a[i],
-
nenhum dos elementos
em a[i+1],...,a[dir] são menores do que a[i].
Exemplo
-
Ordenação
do vetor inicial 25 57 48 37 12 92 86 33.
-
Se o primeiro elemento
(25) for colocado na sua posição correta, teremos: 12 25
57 48 37 92 86 33.
Neste ponto:
-
todos os elementos
abaixo de 25 serão menores e
-
todos os elementos
acima de 25 serão maiores que 25.
-
Como 25 está
na sua posição final, o problema foi decomposto na ordenação
dos subvetores: (12) e (57 48 37 92 86 33).
-
O subvetor (12) já
está classificado.
-
Agora o vetor pode
ser visualizado: 12 25 (57 48 37 92 86 33).
-
Repetir o processo
para a[2]...a[7] resulta em:
12 25 (48 37 33) 57 (92 86)
-
Se continuarmos particionando
12 25 (48 37 33) 57 (92 86), teremos:
-
12 25 (37 33) 48 57
(92 86)
-
12 25 (33) 37 48 57
(92 86)
-
12 25 33 37 48 57
(92 86)
-
12 25 33 37 48 57
(86) 92
-
12 25 33 37 48 57
86 92
Visão
da Recursividade do Quicksort como Árvore:

Método
para o Particionamento
-
Considere x=a[limInf]
como o elemento cuja posição final é a procurada.
-
Usar sempre o primeiro
é só um artifício p/facilitar a implementação.
-
Dois ponteiros alto
e baixo são incializados como os limites máximo e mínimo
do subvetor que vamos analisar.
-
Em qualquer ponto
da execução, todo elemento acima de alto é maior do
que x e todo elemento abaixo de baixo é menor do que x.
-
Os dois ponteiros
alto e baixo são movidos um em direção ao outro da
seguinte forma:
-
1. Incremente baixo
em uma posição até que a[baixo] > x.
-
2. Decremente alto
em uma posição até que a[alto] <= x.
-
3. Se a alto > baixo
, troque a[baixo] por a[alto].
-
O processo é
repetido até que a condição descrita em 3. falhe (quando
alto <= baixo ). Neste ponto a[alto]será
trocado por a[limInf],cuja posição final era procurada,
e alto é retornado em i.
Algoritmo
de Particionamento
inteiro partição(tipoInfo : a[], inteiro : limInf, limSup)
variáveis
tipoInfo : x, temp; inteiro : baixo, alto;
início
x <- a[limInf]; alto <- limSup; baixo <- limInf + 1;
enquanto (baixo < alto) faça
enquanto (a[baixo] <= x E baixo < limSup) faça
incremente baixo; /* Sobe no arquivo */
enquanto (a[alto] > x) faça
decremente alto; /* Desce no arquivo */
se (baixo < alto) então /* Troca */
temp <- a[baixo];
a[baixo] <- a[alto];
a[alto] <- temp;
fim se
fim enquanto
a[limInf] <- a[alto];
a[alto] <- x;
retorne alto;
fim
Comentários
sobre o Quicksort
-
Para evitar o pior
caso e casos ruins onde elementos estão em grupos ordenados pode-se
utilizar uma estratégia probabilística:
-
Selecione, ao invés
do primeiro elemento para ser a, um elemento aleatório. Critérios:
-
Seleção
totalmente randômica: selecione qualquer elemento do subvetor
usando um gerador de números aleatórios.
-
Desvantagem: tempo
de processamento extra para o gerador.
-
Seleção
pseudorandômica: selecione um elemento do subvetor com base em
um cálculo qualquer baseado em valores que você tem à
mão (alto, baixo, chave do primeiro)
-
Seleção
média: pegue ao invés do elemento inicial, sempre o do
meio.
-
Todos estes métodos
melhoram a performance média.
9.3
HeapSort
-
O HeapSort, também
chamado de Classificação por Monte ou Ordenação
com Árvore-Heap é um método de ordenação
que utiliza uma árvore-heap como estrutura intermediária
para efetuar a ordenação.
-
Vantagens:
-
O pior caso é
O(n log n). Os outros são um pouco, porém muito pouco, melhores.
-
HeapSort é
mais estável que Quicksort.
-
Desvantagens:
-
Construir a árvore-heap
pode consumir muita memória.
-
Em suma:
-
Para dados bem bagunçados
o Quicksort é mais vantajoso por ser mais econômico.
-
Para dados imprevisíveis,
pode ser mais vantajoso por ser previsível em termos de tempo de
execução.
9.3.1
Preâmbulo: Árvore Heap
-
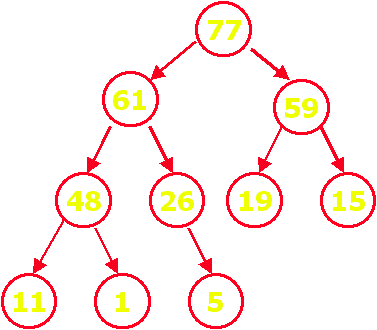
Def.: Uma árvore-heap,
também chamada de monte é uma árvore binária
por níveis, onde o nodo pai de uma subárvore sempre é
maior que todos os seus descendentes.
-
Exemplo:
9.3.2
Método em HeapSort
É um método
em três estágios:
-
Primeiramente criamos
uma visão sobre o arquivo como árvore binária por
níveis.
-
Iterativamente:
-
Reestruturamos o
arquivo para para que se transforme em um monte.
-
Na terceira etapa
geramos a seqüência de saída retirando a raiz do monte
e reestruturando o monte para que retorne a satisfazer a condição-heap.
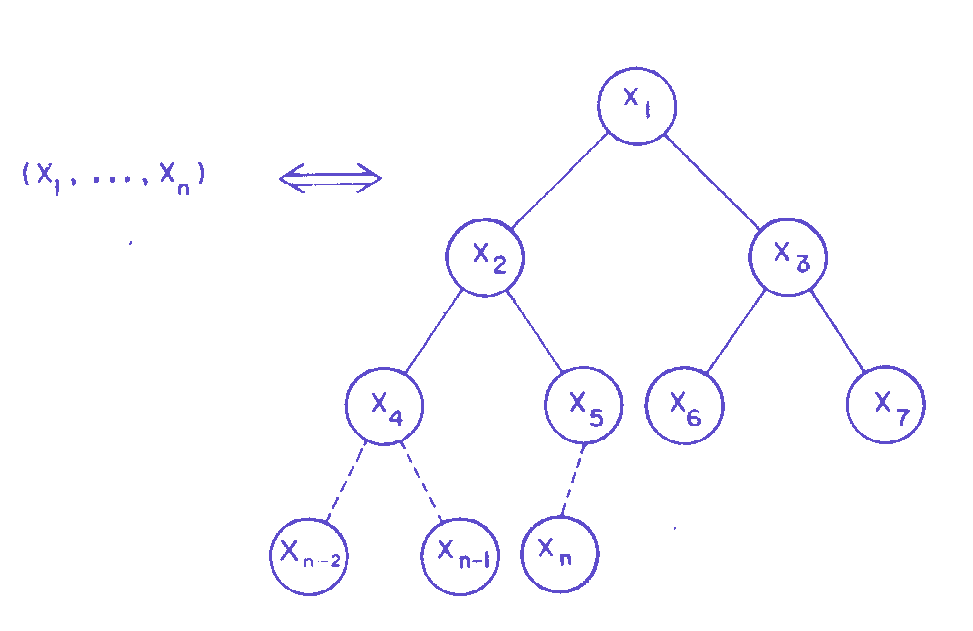
Visão do arquivo
x1,...xn por Níveis:
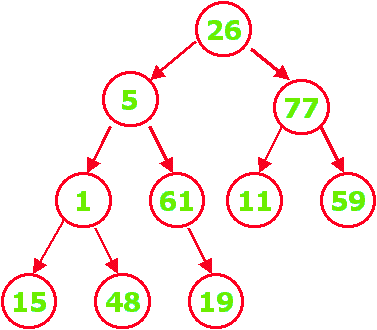
Árvore-Heap a partir
do Arquivo
(26
5 77 1 61 11 59 15 48 19)
|
Arquivo Original por Níveis
|
Árvore Heap Resultante
|
 |
 |
Algoritmo
HeapSort
heapsort( tipoInfo : a[], inteiro : n)
variáveis
inteiro : i;
tipoInfo : temp;
início
para I de (n div 2) até 1 passo -1 faça
ajuste(a, I, n); /* Converta a em um heap */
fim para
para I de (n-1) até 1 passo -1 faça
temp <- a[I+1];
a[I+1] <- a[1]; /* Supõe posição inicial = 1 */
a[1] <- temp;
ajuste(a,1,I); /* Restabeleça o heap */
fim para
fim
Algoritmo
do Ajuste
ajuste( tipoInfo : a[], inteiro : i, n)
variáveis
inteiro : j;
tipoInfo : aAux;
início
aAux <- a[i] /* Supõe posição inicial = 1 */
j <- 2*i;
enquanto j <= n faça
se j < n E a[j] < a[j+1] então
incremente j;
fim se
se aAux >= a[j] então
retorne
fim se
a[j div 2] <- a[j];
a[j] <- aAux; /* falta no algoritmo dado em
Horowitz&Sahni */
j <- 2*j;
fim enquanto
a[j div 2] <- aAux;
fim
9.4
Exercícios
-
Execute o algoritmo
de particionamento no papel para o exemplo de arquivo dado no exemplo de
QuickSort.
-
Execute o algoritmo
do HeapSort sobre o mesmo exemplo. Mostre o arquivo a cada iteração
do ajuste.
-
Escolha e implemente
em C++ um dos dois algoritmos dados.
-
A implementação
deve ser capaz de ler um arquivo contendo uma série de números
reais, um por linha.
-
A implementação
deverá ser capaz de escrever em um arquivo o tempo necessário
para ordenar os dados, no mesmo formato pedido par
-
a a árvore.
-
Diferença:
serão fornecidos diversos arquivos. O tempo deverá ser escrito
sempre no fim de um arquivo só.








